Skip to main content

Advertisement

Springer Nature Link
Log in

Ultimate bound and optimal measurement for estimation of coupling constant in Tavis–Cummings model

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

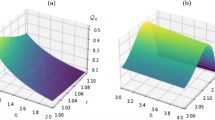
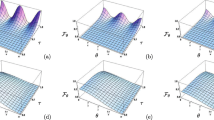
We seek to study the problem of estimating the atoms-field coupling constant in Tavis–Cummings model for interaction between two atoms and an electromagnetic field by means of local estimation theory. We calculate the quantum Fisher information (QFI) for the most general pure probe state that undergoes evolution generated by the Hamiltonian of the Tavis–Cummings model; then, proper probe states which maximize the QFI are determined. Furthermore, we consider subspaces separately and show that QFI for atomic subspace (contains both qubits) and cavity field subspace can reach the maximum value of QFI in the whole space by choosing proper initial state. Finally, the optimal measurement that saturates the Cramer–Rao bound, i.e., the measurement with Fisher information equal to QFI, for considered states are determined in the whole space and the subspaces, separately.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Dicke, R.H.: Coherence in spontaneous radiation processes. Phys. Rev. 93, 99 (1954)

    Article  ADS  Google Scholar 

  2. Tavis, M., Cummings, F.W.: Exact solution for an \(N\)-molecule—radiation-field Hamiltonian. Phys. Rev. 170, 379 (1968)

    Article  ADS  Google Scholar 

  3. Tavis, M., Cummings, F.W.: Approximate solutions for an \(N\)-molecule-radiation-field Hamiltonian. Phys. Rev. 188, 692 (1969)

    Article  ADS  Google Scholar 

  4. Bogoliubov, N.M., Bullough, R.K., Timonen, J.: Exact solution of generalized Tavis–Cummings models in quantum optics. J. Phys. A Math. Gen. 29, 6305 (1996)

    Article  ADS  MathSciNet  Google Scholar 

  5. Dukelsky, J., Dussel, G.G., Esebbag, C., Pittel, S.: Exactly solvable models for atom–molecule Hamiltonians. Phys. Rev. Lett. 93, 050403 (2004)

    Article  ADS  MathSciNet  Google Scholar 

  6. He, M.-M., Chen, G., Liang, J.-Q.: Berry phase in Tavis–Cummings model. Eur. Phys. J. D 44, 581 (2007)

    Article  ADS  MathSciNet  Google Scholar 

  7. Hassan, S.S., SebaweAbdalla, M., Obada, A.-S.F., Batarfi, H.A.: Periodic squeezing in the Tavis–Cummings model. J. Mod. Opt. 40, 1351 (1993)

    Article  ADS  MathSciNet  Google Scholar 

  8. Tessier, T.E., Deutsch, I.H., Delgado, A., Fuentes-Guridi, I.: Entanglement sharing in the two-atom Tavis–Cummings model. Phys. Rev. A 68, 062316 (2003)

    Article  ADS  Google Scholar 

  9. Knap, M., Arrigoni, E., von der Linden, W.: Quantum phase transition and excitations of the Tavis–Cummings lattice model. Phys. Rev. B 82, 045126 (2010)

    Article  ADS  Google Scholar 

  10. Zou, J.H., Liu, T., Feng, M., Yang, W.L., Chen, C.Y., Twamley, J.: Quantum phase transition in a driven Tavis–Cummings model. New J. Phys. 15, 123032 (2013)

    Article  ADS  Google Scholar 

  11. Leek, P.J., Filipp, S., Maurer, P., Baur, M., Bianchetti, R., Fink, J.M., Göppl, M., Steffen, L., Wallraff, A.: Using sideband transitions for two-qubit operations in superconducting circuits. Phys. Rev. B 79, 180511(R) (2009)

    Article  ADS  Google Scholar 

  12. Youssef, M., Metwally, N., Obada., A.-S.F.: Some entanglement features of a three-atom Tavis–Cummings model: a cooperative case. J. Phys. B At. Mol. Opt. Phys. 43, 095501 (2010)

    Article  ADS  Google Scholar 

  13. Cai, J.-F., Liu, H.-P., and: Entanglement in three-atom Tavis–Cummings model induced by a thermal field. Commun. Theor. Phys. 43, 427 (2005)

    Article  ADS  Google Scholar 

  14. Hou, X.-W., Wan, M.-F., Ma, Z.-Q.: Tripartite entanglement dynamics for mixed states in the Tavis–Cummings model with intrinsic decoherence. Eur. Phys. J. D 66, 152 (2012)

    Article  ADS  Google Scholar 

  15. Ma, J.-M., Jiao, Z.-Y., Li, N.: Quantum entanglement in two-photon Tavis–Cummings model with a Kerr nonlinearity. Int. J. Theor. Phys. 46, 2550 (2007)

    Article  MathSciNet  Google Scholar 

  16. López, C.E., Lastra, F., Romero, G., Retamal, J.C.: Entanglement properties in the inhomogeneous Tavis–Cummings model. Phys. Rev. A 75, 022107 (2007)

    Article  ADS  MathSciNet  Google Scholar 

  17. Chuan-Jia, S., Yun-Jie, X.: The entanglement character of two entangled atoms in Tavis–Cummings model. Acta Phys. Sin. 55, 01585 (2006)

    Google Scholar 

  18. Jarvis, C.E.A., Rodrigues, D.A., Györffy, B.L., Spiller, T.P., Short, A.J., Annett, J.F.: Dynamics of entanglement and ‘attractor’ states in the Tavis–Cummings model. New J. Phys. 11, 103047 (2009)

    Article  ADS  Google Scholar 

  19. Zhang, Y.Q., Xu, J.B.: Dynamics of quantum discord in two Tavis–Cummings models with classical driving fields. Eur. Phys. J. D 64, 549 (2011)

    Article  ADS  Google Scholar 

  20. He, Q.-L., Jing-Bo, X.: Enhancement of stationary state quantum discord in Tavis–Cummings model by nonlinear Kerr-like medium. Opt. Commun. 284, 3649 (2011)

    Article  ADS  Google Scholar 

  21. Cramer, H.: Mathematical Methods of Statistics. Princeton University Press, Princeton (1946)

    MATH  Google Scholar 

  22. Helstrom, C.W.: Quantum Detection and Estimation Theory. Academic Press, New York (1976)

    MATH  Google Scholar 

  23. Holevo, A.S.: Statistical Structure of Quantum Theory. Lecture Notes in Physics 61. Springer, Berlin (2001)

    Book  Google Scholar 

  24. Braunstein, S., Caves, C.: Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 72, 3439 (1994)

    Article  ADS  MathSciNet  Google Scholar 

  25. Braunstein, S., Caves, C., Milburn, G.: Generalized uncertainty relations: theory, examples, and Lorentz invariance. Ann. Phys. 247, 135 (1996)

    Article  ADS  MathSciNet  Google Scholar 

  26. Paris, M.G.A.: Quantum estimation for quantum technology. Int. J. Quantum Inf. 7, 125 (2009)

    Article  Google Scholar 

  27. Ragy, S., Jarzyna, M., Demkowicz-Dobrzanski, R.: Compatibility in multiparameter quantum metrology. Phys. Rev. A 94, 052108 (2016)

    Article  ADS  Google Scholar 

  28. Virzì, S., et al.: Optimal estimation of parameters of an entangled quantum state. J. Phys. Conf. Ser. 841, 012033 (2017)

    Article  Google Scholar 

  29. Sun, Z., Ma, J., Xiao-Ming, L., Wang, X.: Fisher information in a quantum-critical environment. Phys. Rev. A 82, 022306 (2010)

    Article  ADS  Google Scholar 

  30. Wang, T.-L., Ling-Na, W., Yang, W., Jin, G.-R., Lambert, N., Nori, F.: Quantum Fisher information as a signature of the superradiant quantum phase transition. New J. Phys. 16, 063039 (2014)

    Article  ADS  MathSciNet  Google Scholar 

  31. Armata, F., Latmiral, L., Plato, A.D.K., Kim, M.S.: Quantum limits to gravity estimation with optomechanics. Phys. Rev. A 96, 043824 (2017)

    Article  ADS  Google Scholar 

  32. Fujiwara, A.: Quantum channel identification problem. Phys. Rev. A 63, 042304 (2001)

    Article  ADS  Google Scholar 

  33. Fujiwara, A., Imai, H.: Quantum parameter estimation of a generalized Pauli channel. J. Phys. A 36, 8093 (2003)

    Article  ADS  MathSciNet  Google Scholar 

  34. Ji, Z., Wang, G., Duan, R., Feng, Y., Ying, M.: Parameter estimation of quantum channels. IEEE Trans. Inf. Theory 54, 11 (2008)

    Article  MathSciNet  Google Scholar 

  35. Gill, R.D., Massar, S.: State estimation for large ensembles. Phys. Rev. A 61, 042312 (2000)

    Article  ADS  Google Scholar 

  36. Invernizzi, C., Korbman, M., Venuti, L.C., Paris, M.G.A.: Optimal quantum estimation in spin systems at criticality. Phys. Rev. A 78, 042106 (2008)

    Article  ADS  Google Scholar 

  37. Zanardi, P., Paris, M.G.A., Venuti, L.C.: Quantum criticality as a resource for quantum estimation. Phys. Rev. A 78, 042105 (2008)

    Article  ADS  Google Scholar 

  38. Genoni, M.G., Invernizzi, C.: Optimal quantum estimation of the coupling constant of Jaynes–Cummings interaction. Eur. Phys. J. Spec. Top. 203, 49 (2012)

    Article  Google Scholar 

  39. Salvatori, G., Mandarino, A., Paris, M.G.A.: Quantum metrology in Lipkin–Meshkov–Glick critical systems. Phys. Rev. A 90, 022111 (2014)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Physics, Azarbaijan Shahid Madani University, PO Box 53714-161, Tabriz, Iran

    E. Faizi & P. Mahmoudi

Authors
  1. E. Faizi
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. P. Mahmoudi
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to E. Faizi.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Faizi, E., Mahmoudi, P. Ultimate bound and optimal measurement for estimation of coupling constant in Tavis–Cummings model. Quantum Inf Process 17, 303 (2018). https://doi.org/10.1007/s11128-018-2074-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-018-2074-8

Keywords