Construction of quantum gates for concatenated Greenberger–Horne–Zeilinger-type logic qubit

Abstract

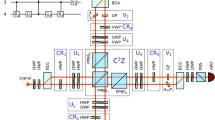
Concatenated Greenberger–Horne–Zeilinger (C-GHZ) state is a kind of logic qubit which is robust in noisy environment. In this paper, we encode the C-GHZ state as the logic qubit and design two kinds of quantum gates for such logic qubit. The first kind is the single logic-qubit gate which contains the logic-qubit bit-flip gate and phase-flip gate. The second kind is the logic-qubit controlled-not (CNOT) gate. We exploit the single quantum gate for physical qubit, such as bit-flip gate and phase-flip gate, and two-qubit CNOT gate to realize the logic-qubit gate. We also calculated the success probability of such logic-qubit gate based on the imperfect physical quantum gate. This protocol may be useful for future quantum computation.

Appendix A: Simplification of the EL qubits \(|\bar{0}\rangle _{m,N}\) and \(|\bar{1}\rangle _{m,N}\)

The state in Eq. (2) can be simplified to the state in Eq. (3). The simplification process is shown as follows

$$\begin{aligned} |\bar{0}\rangle _{m,N}= & {} \frac{1}{\sqrt{2}}\left( \left| \hbox {GHZ}_{m}^{+}\right\rangle ^{\otimes N}+\left| \hbox {GHZ}_{m}^{-}\right\rangle ^{\otimes N}\right) \nonumber \\= & {} \frac{1}{\sqrt{2}}\left( \left( \frac{1}{\sqrt{2}}\right) ^{N}\left( |0\rangle ^{\otimes m}+|1\rangle ^{\otimes m}\right) ^{\otimes N}+\left( \frac{1}{\sqrt{2}}\right) ^{N}\left( |0\rangle ^{\otimes m}-|1\rangle ^{\otimes m}\right) ^{\otimes N} \right) \nonumber \\= & {} \left( \frac{1}{\sqrt{2}}\right) ^{N+1}\left( \left( |0\rangle ^{\otimes m}+|1\rangle ^{\otimes m}\right) ^{\otimes N}+\left( |0\rangle ^{\otimes m}-|1\rangle ^{\otimes m}\right) ^{\otimes N}\right) . \end{aligned}$$

(27)

The constant $({\sqrt{2}})^{N + 1}$ can be represented by the letter $\bar{C}$.

$$\begin{aligned} \bar{C}|\bar{0}\rangle _{m,N}= & {} {\left( {{{\left| 0 \right\rangle }^{ \otimes m}} + {{\left| 1 \right\rangle }^{ \otimes m}}} \right) _1}{\left( {{{\left| 0 \right\rangle }^{ \otimes m}} + {{\left| 1 \right\rangle }^{ \otimes m}}} \right) _2} \cdots {\left( {{{\left| 0 \right\rangle }^{ \otimes m}} + {{\left| 1 \right\rangle }^{ \otimes m}}} \right) _N} \nonumber \\&+\, {\left( {{{\left| 0 \right\rangle }^{ \otimes m}} - {{\left| 1 \right\rangle }^{ \otimes m}}} \right) _1}{\left( {{{\left| 0 \right\rangle }^{ \otimes m}} - {{\left| 1 \right\rangle }^{ \otimes m}}} \right) _2} \cdots {\left( {{{\left| 0 \right\rangle }^{ \otimes m}} - {{\left| 1 \right\rangle }^{ \otimes m}}} \right) _N}. \end{aligned}$$

(28)

Here, ${\left| 0 \right\rangle }^{ \otimes m}$ and ${\left| 1 \right\rangle }^{ \otimes m}$ are block qubits which will be represented as letter A and letter B. Each block qubit contains m physical qubits. The subscripts 1, 2, $\ldots$ , N indicate the serial number of the block qubit. In order to simplify the calculation, ${\left| 0 \right\rangle }^{ \otimes m}$ and ${\left| 1 \right\rangle }^{ \otimes m}$ shown in ${\left( {{{\left| 0 \right\rangle }^{ \otimes m}} + {{\left| 1 \right\rangle }^{ \otimes m}}} \right) _1}$ or ${\left( {{{\left| 0 \right\rangle }^{ \otimes m}} - {{\left| 1 \right\rangle }^{ \otimes m}}} \right) _1}$ can be marked as ${A_1}$ and ${B_1}$. Thus, Eq. (28) can be written as

$$\begin{aligned} \bar{C}|\bar{0}\rangle _{m,N}= & {} {\left( {{A_1} + {B_1}} \right) }{\left( {{{\left| 0 \right\rangle }^{ \otimes m}} + {{\left| 1 \right\rangle }^{ \otimes m}}} \right) _2} \cdots {\left( {{{\left| 0 \right\rangle }^{ \otimes m}}+ {{\left| 1 \right\rangle }^{ \otimes m}}} \right) _N}\nonumber \\&+\, {\left( {{A_1} - {B_1}} \right) }{\left( {{{\left| 0 \right\rangle }^{ \otimes m}} - {{\left| 1 \right\rangle }^{ \otimes m}}} \right) _2} \cdots {\left( {{{\left| 0 \right\rangle }^{ \otimes m}} - {{\left| 1 \right\rangle }^{ \otimes m}}} \right) _N}\nonumber \\= & {} {\left( {{A_1}{{\left| 0 \right\rangle }^{ \otimes m}} + {B_1}{{\left| 1 \right\rangle }^{ \otimes m}} + {A_1}{{\left| 1 \right\rangle }^{ \otimes m}} + {B_1}{{\left| 0 \right\rangle }^{ \otimes m}}} \right) _{2'}}\nonumber \\&\cdots {\left( {{{\left| 0 \right\rangle }^{ \otimes m}} + {{\left| 1 \right\rangle }^{ \otimes m}}} \right) _N}\nonumber \\&+\, {\left( {{A_1}{{\left| 0 \right\rangle }^{ \otimes m}} + {B_1}{{\left| 1 \right\rangle }^{ \otimes m}} - {A_1}{{\left| 1 \right\rangle }^{ \otimes m}} - {B_1}{{\left| 0 \right\rangle }^{ \otimes m}}} \right) _{2'}}\nonumber \\&\cdots {\left( {{{\left| 0 \right\rangle }^{ \otimes m}} - {{\left| 1 \right\rangle }^{ \otimes m}}} \right) _N}. \end{aligned}$$

(29)

Here, the subscripts $2'$ indicates that the expression within parentheses comes from the first two items. Next, we define the ${A_1}{{\left| 0 \right\rangle }^{ \otimes m}} + {B_1}{{\left| 1 \right\rangle }^{ \otimes m}}$ as $A_{2}$ and the ${A_1}{{\left| 1 \right\rangle }^{ \otimes m}} + {B_1}{{\left| 0 \right\rangle }^{ \otimes m}}$ as $B_{2}$. Since $A_1$ does not contain the block qubit B, ${A_1}{{\left| 0 \right\rangle }^{ \otimes m}}$ also does not contain the item B. Similarly, the ${B_1}{{\left| 1 \right\rangle }^{ \otimes m}}$ contains two such block qubits. Therefore, the $A_2$ contains an even number of block qubit B. $B_2$ contains an odd number of B. In this way, the equation can be rewritten as

$$\begin{aligned} \bar{C}|\bar{0}\rangle _{m,N}= & {} \left( {{A_2} + {B_2}} \right) \cdots {\left( {{{\left| 0 \right\rangle }^{ \otimes m}} + {{\left| 1 \right\rangle }^{ \otimes m}}} \right) _N}\nonumber \\&+\, \left( {{A_2} - {B_2}} \right) \cdots {\left( {{{\left| 0 \right\rangle }^{ \otimes m}} - {{\left| 1 \right\rangle }^{ \otimes m}}} \right) _N}. \end{aligned}$$

(30)

By using a similar iterative approach, Eq. (28) eventually becomes:

$$\begin{aligned} \bar{C}|\bar{0}\rangle _{m,N}= & {} \left( {{A_{N - 1}} + {B_{N - 1}}} \right) {\left( {{{\left| 0 \right\rangle }^{ \otimes m}} + {{\left| 1 \right\rangle }^{ \otimes m}}} \right) _N}\nonumber \\&+\, \left( {{A_{N - 1}} - {B_{N - 1}}} \right) {\left( {{{\left| 0 \right\rangle }^{ \otimes m}} - {{\left| 1 \right\rangle }^{ \otimes m}}} \right) _N}\nonumber \\= & {} 2{A_{N - 1}}\left| 0 \right\rangle _N^{ \otimes m} + 2{B_{N - 1}}\left| 1 \right\rangle _N^{ \otimes m}. \end{aligned}$$

(31)

Here, $A_{N - 1}$ contains an even number of block qubits B and $B_{N - 1}$ contains an odd number of block qubits B. These two algebraic expressions can be expressed in the following

$$\begin{aligned} {A_{N - 1}}= & {} \sum \limits _{{x_i} \in {X_0}} {\prod \limits _{i = 1}^{N - 1} {{{\left| {{x_i}} \right\rangle }^{ \otimes m}}} } ,{X_\mathrm{{0}}}\mathrm{{ = }}\left\{ {{x_i} \in \{ 0,1\} \left| {\sum \limits _{i = 1}^{N - 1} {{x_i} = \mathrm{{0}}( {\bmod 2} )} } \right. } \right\} \nonumber \\ {B_{N - 1}}= & {} \sum \limits _{{x_i} \in {X_1}} {\prod \limits _{i = 1}^{N - 1} {{{\left| {{x_i}} \right\rangle }^{ \otimes m}}} } ,{X_1}\mathrm{{ = }}\left\{ {{x_i} \in \{ 0,1\} \left| {\sum \limits _{i = 1}^{N - 1} {{x_i} = 1( {\bmod 1} )} } \right. } \right\} . \end{aligned}$$

(32)

Finally, after simplifying the EL qubits $|\bar{0}\rangle _{m,N}$ and $|\bar{1}\rangle _{m,N}$, Eq. (31) can be written as:

$$\begin{aligned} |\bar{0}\rangle _{m,N}= & {} {\left( {\frac{1}{{\sqrt{2} }}}\right) ^{N - 1}}\left( {{A_{N-1}}{{\left| 0 \right\rangle }^{ \otimes m}} + {B_{N-1}}{{\left| 1 \right\rangle }^{ \otimes m}}} \right) ,\nonumber \\ |\bar{1}\rangle _{m,N}= & {} {\left( {\frac{1}{{\sqrt{2} }}}\right) ^{N - 1}}\left( {{B_{N-1}}{{\left| 0 \right\rangle }^{ \otimes m}} + {A_{N-1}}{{\left| 1 \right\rangle }^{ \otimes m}}} \right) . \end{aligned}$$

(33)

For example, $|\bar{0}\rangle _{m,N}$ with $m=2,N=3$ can be written as

$$\begin{aligned} |\bar{0}{\rangle _{2,3}}= & {} {\left( {\frac{{\text {1}}}{{\sqrt{\text {2}} }}} \right) ^{\text {2}}}\left( {{{\left( {{{\left| {\text {0}} \right\rangle }^{ \otimes {\text {2}}}}{\text { + }}{{\left| {\text {1}} \right\rangle }^{ \otimes {\text {2}}}}} \right) }^{ \otimes {\text {3}}}}{\text { + }}{{\left( {{{\left| {\text {0}} \right\rangle }^{ \otimes {\text {2}}}} - {{\left| {\text {1}} \right\rangle }^{ \otimes {\text {2}}}}} \right) }^{ \otimes {\text {3}}}}} \right) \nonumber \\= & {} {\left( {\frac{{\text {1}}}{{\sqrt{\text {2}} }}} \right) ^{\text {2}}}\left( \left( {\left| {{\text {00}}} \right\rangle {\text { + }}\left| {{\text {11}}} \right\rangle } \right) \left( {\left| {{\text {00}}} \right\rangle {\text { + }}\left| {{\text {11}}} \right\rangle } \right) \left( {\left| {{\text {00}}} \right\rangle {\text { + }}\left| {{\text {11}}} \right\rangle } \right) \right. \nonumber \\&\left. +\, \left( {\left| {{\text {00}}} \right\rangle - \left| {{\text {11}}} \right\rangle } \right) \left( {\left| {{\text {00}}} \right\rangle - \left| {{\text {11}}} \right\rangle } \right) \left( {\left| {{\text {00}}} \right\rangle - \left| {{\text {11}}} \right\rangle } \right) \right) \nonumber \\= & {} {\frac{{\text {1}}}{2}} \left( \left| {{\text {000000}}} \right\rangle +\left| {{\text {001111}}} \right\rangle +\left| {{\text {110011}}}\right\rangle +\left| {{\text {111100}}} \right\rangle \right) \nonumber \\= & {} {\frac{{\text {1}}}{2}}\left( \left( \left| 0000\right\rangle + \left| 1111\right\rangle \right) \left| 0\right\rangle ^{\otimes {2}}+ \left( \left| 0011\right\rangle + \left| 1100\right\rangle \right) \left| 1\right\rangle ^{\otimes {2}} \right) . \end{aligned}$$

(34)

Here $A_{2}=( \left| 00\right\rangle \left| 00\right\rangle + \left| 11\right\rangle \left| 11\right\rangle )$ and $B_{2}=( \left| 00\right\rangle \left| 11\right\rangle + \left| 11\right\rangle \left| 00\right\rangle )$.