Two-time correlation functions of a two-level system influenced by a composite environment

Abstract

To study the quantum regression theorem and the Leggett–Garg inequality, two-time correlation functions are calculated for a two-level system which is placed under the influence of a composite environment consisting of two subsystems. Two different configurations, I and II, are considered. In the configuration I, a two-level system of interest interacts with a thermal reservoir via another two-level system. In the configuration II, a relevant two-level system is influenced independently by another two-level system and a thermal reservoir. In both configurations, the thermal reservoir is assumed to have a sufficiently short correlation time. When an interacting nuclear-spin and electron-spin system is considered, the relevant system is a nuclear-spin (electron-spin) in the configuration I (II). It is shown that the quantum regression theorem for the relevant two-level system is always valid in the configuration II while it is not in the configuration I, regardless of whether the reduced time evolution is Markovian or not. Furthermore, it is found that the Leggett–Garg inequality can be violated in both configurations. The dependence of the violation on the parameters characterizing the open two-level system is investigated.

Appendices

Derivation of Eqs. (8)–(11)

In this appendix, we provide a brief derivation of Eqs. (8)–(11). In the interaction picture, the quantum master equation (2) becomes

$$\begin{aligned} \frac{\partial }{\partial t}\tilde{W}_{AB}(t)= & {} -ig[\sigma _{A}^{z}\sigma _{B}^{z},\tilde{W}_{AB}(t)] +\frac{1+w}{4T_{1}}([\sigma _{B}^{+},\tilde{W}_{AB}(t)\sigma _{B}^{-}] +[\sigma _{B}^{+}\tilde{W}_{AB}(t),\sigma _{B}^{-}])\nonumber \\&+\frac{1-w}{4T_{1}}([\sigma _{B}^{-},\tilde{W}_{AB}(t)\sigma _{B}^{+}] +[\sigma _{B}^{-}\tilde{W}_{AB}(t),\sigma _{B}^{+}])\nonumber \\&+\frac{1}{4}\left( \frac{1}{2T_{1}}-\frac{1}{T_{2}}\right) [\sigma _{B}^{z},[\sigma _{B}^{z},\tilde{W}_{AB}(t)]], \end{aligned}$$

(64)

where we set $\tilde{W}_{AB}(t) =e^{i\omega _{A}t\sigma _{A}^{z}+i\omega _{B}t\sigma _{B}^{z}}W_{AB}(t) e^{-i\omega _{A}t\sigma _{A}^{z}+i\omega _{B}t\sigma _{B}^{z}}$. Then we obtain the equations of motion for the operators $\tilde{W}_{A}^{jk}(t) ={}_{B}\langle j\vert \tilde{W}_{AB}(t)\vert k\rangle _{B}$ of the system A,

$$\begin{aligned} \frac{\partial }{\partial t}\tilde{W}_{A}^{ee}(t)= & {} -ig\sigma _{A}^{\times }\tilde{W}_{A}^{ee}(t) -\frac{1-w}{2T_{1}}\tilde{W}_{A}^{ee}(t) +\frac{1+w}{2T_{1}}\tilde{W}_{A}^{gg}(t), \end{aligned}$$

(65)

$$\begin{aligned} \frac{\partial }{\partial t}\tilde{W}_{A}^{gg}(t)= & {} ig\sigma _{A}^{\times }\tilde{W}_{A}^{gg}(t) -\frac{1+w}{2T_{1}}\tilde{W}_{A}^{gg}(t) +\frac{1-w}{2T_{1}}\tilde{W}_{A}^{ee}(t), \end{aligned}$$

(66)

$$\begin{aligned} \frac{\partial }{\partial t}\tilde{W}_{A}^{eg}= & {} \left( -ig\sigma _{A}^{\circ }-\frac{1}{T_{2}}\right) \tilde{W}_{A}^{eg}(t), \end{aligned}$$

(67)

$$\begin{aligned} \frac{\partial }{\partial t}\tilde{W}_{A}^{ge}= & {} \left( ig\sigma _{A}^{\circ }-\frac{1}{T_{2}}\right) \tilde{W}_{A}^{ge}(t). \end{aligned}$$

(68)

The latter two equations yield the solutions,

$$\begin{aligned} \tilde{W}_{A}^{eg}(t)=e^{-igt\sigma _{A}^{\circ }-t/T_{2}}W_{A}^{eg}(0), \quad \quad \quad \tilde{W}_{A}^{ge}(t)=e^{igt\sigma _{A}^{\circ }-t/T_{2}}W_{A}^{eg}(0). \end{aligned}$$

(69)

On the other hand, Eqs. (65) and (66) are rewritten into

$$\begin{aligned} \frac{\partial }{\partial t} \left( \begin{array}{c} \tilde{W}_{A}^{ee}(t) \\ \tilde{W}_{A}^{gg}(t) \end{array}\right) =\mathsf {M} \left( \begin{array}{c} \tilde{W}_{A}^{ee}(t) \\ \tilde{W}_{A}^{gg}(t) \end{array}\right) , \end{aligned}$$

(70)

with

$$\begin{aligned} \mathsf {M}=\left( \begin{array}{cc} \displaystyle {-ig\sigma _{A}^{\times }-\frac{1-w}{2T_{1}}} &{} \displaystyle {\frac{1+w}{2T_{1}}} \\ \displaystyle {\frac{1-w}{2T_{1}}} &{} \displaystyle {ig\sigma _{A}^{\times }-\frac{1+w}{2T_{1}}} \end{array}\right) . \end{aligned}$$

(71)

The matrix $\mathsf {M}$ is diagonalized as

$$\begin{aligned} \mathsf {U}^{-1}\mathsf {M}\mathsf {U} =\left( \begin{array}{cc} \displaystyle {-\frac{1+a(\sigma _{A}^{\times })}{2T_{1}}} &{} 0 \\ 0 &{} \displaystyle {-\frac{1-a(\sigma _{A}^{\times })}{2T_{1}}} \end{array}\right) , \end{aligned}$$

(72)

with

$$\begin{aligned} \mathsf {U}= & {} \left( \begin{array}{cc} \displaystyle {\frac{1+w}{2T_{1}}} &{} \displaystyle {\frac{1+w}{2T_{1}}} \\ \displaystyle {ig\sigma _{A}^{\times } -\frac{w+a(\sigma _{A}^{\times })}{2T_{1}}} &{} \displaystyle {ig\sigma _{A}^{\times } -\frac{w-a(\sigma _{A}^{\times })}{2T_{1}}} \end{array}\right) , \end{aligned}$$

(73)

$$\begin{aligned} \mathsf {U}^{-1}= & {} \frac{2T_{1}^{2}}{(1+w)a(\sigma _{A}^{\times })} \left( \begin{array}{cc} \displaystyle {ig\sigma _{A}^{\times } -\frac{w-a(\sigma _{A}^{\times })}{2T_{1}}} &{} -\displaystyle {\frac{1+w}{2T_{1}}} \\ \displaystyle {-ig\sigma _{A}^{\times } +\frac{w+a(\sigma _{A}^{\times })}{2T_{1}}} &{} \displaystyle {\frac{1+w}{2T_{1}}} \end{array}\right) , \end{aligned}$$

(74)

where $a(\sigma _{A}^{\times })$ is given by Eq. (12). Thus, the solution of Eq. (70) is given by

$$\begin{aligned} \left( \begin{array}{c} W_{A}^{ee}(t) \\ W_{A}^{gg}(t) \end{array}\right) =\left( \begin{array}{cc} V_{11}(t) &{} V_{12}(t) \\ V_{21}(t) &{} V_{22}(t) \end{array}\right) \left( \begin{array}{c} W_{A}^{ee}(0) \\ W_{A}^{gg}(0) \end{array}\right) , \end{aligned}$$

(75)

with

$$\begin{aligned} V_{11}(t)= & {} e^{-t/2T_{1}}\left[ \cosh \left( \frac{a(\sigma _{A}^{\times })t}{2T_{1}}\right) +\frac{w-2igT_{1}\sigma _{A}^{\times }}{a(\sigma _{A}^{\times })} \sinh \left( \frac{a(\sigma _{A}^{\times })t}{2T_{1}}\right) \right] , \end{aligned}$$

(76)

$$\begin{aligned} V_{12}(t)= & {} e^{-t/2T_{1}}\left( \frac{1+w}{a(\sigma _{A}^{\times })}\right) \sinh \left( \frac{a(\sigma _{A}^{\times })t}{2T_{1}}\right) , \end{aligned}$$

(77)

$$\begin{aligned} V_{21}(t)= & {} e^{-t/2T_{1}}\left( \frac{1-w}{a(\sigma _{A}^{\times })}\right) \sinh \left( \frac{a(\sigma _{A}^{\times })t}{2T_{1}}\right) , \end{aligned}$$

(78)

$$\begin{aligned} V_{22}(t)= & {} e^{-t/2T_{1}}\left[ \cosh \left( \frac{a(\sigma _{A}^{\times })t}{2T_{1}}\right) -\frac{w-2igT_{1}\sigma _{A}^{\times }}{a(\sigma _{A}^{\times })} \sinh \left( \frac{a(\sigma _{A}^{\times })t}{2T_{1}}\right) \right] . \end{aligned}$$

(79)

Finally, we obtain Eqs. (8)–(11) in the Schrödinger picture.

A comment on the quantum regression theorem

Two-time correlation functions can be calculated by the formulas provided in Refs. [23,24,25,26]. In particular, using the formula derived in Ref. [26], we can express the two-time correlation function of quantum operations $X_{1}$ and $X_{2}$ of a relevant system under the influence of a thermal reservoir as

$$\begin{aligned} \langle X_{2}(t_{2})X_{1}(t_{1})\rangle= & {} \mathrm {Tr}[X_{2}\mathscr {V}(t_{2},t_{1})X_{1} \mathscr {V}(t_{1},t_{0}) W(t_{0})]\nonumber \\&+\Delta \langle X_{2}(t_{2})X_{1}(t_{1})\rangle \quad \quad (t_{2}>t_{1}>t_{0}), \end{aligned}$$

(80)

where $W(t_{0})$ is an initial density operator of the relevant system and $\Delta \langle X_{2}(t_{2})X_{1}(t_{1})\rangle$ is a correction term. The reduced density operator W(t) of the relevant quantum system is obtained by solving the time-local quantum master equation [1], $\partial W(t)/\partial t=\mathscr {K}(t)W(t)$, the formal solution of which is given by $W(t)=\mathscr {V}(t,t_{0})W(t_{0})$ with $\mathscr {V}(t,t_{0})=\mathrm {T}\exp \left( \int _{t_{0}}^{t}ds\, \mathscr {K}(s)\right)$. If the second term on the right-hand side of Eq. (80) is negligible, the two-time correlation function can be determined by the solution of the quantum master equation, that is, the quantum channel $\mathscr {V}(t)$. Up to the lowest order with respect to a system–reservoir interaction, the correction term $\Delta \langle X_{2}(t_{2})X_{1}(t_{1})\rangle$ is given in the form of

$$\begin{aligned} \Delta \langle X_{2}(t_{2})X_{1}(t_{1})\rangle =\sum _{jk}\int _{t_{1}}^{t_{2}}d\tau _{2}\int _{t_{0}}^{t_{1}}d\tau _{1}\, \langle R_{j}(\tau _{2})R_{k}(\tau _{1})\rangle _{R} G_{jk}(t_{2},t_{1};\tau _{2},\tau _{1}), \end{aligned}$$

(81)

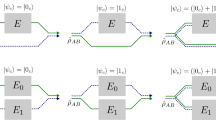
where $\langle R_{j}(\tau _{2})R_{k}(\tau _{1})\rangle _{R}$ is a correlation function of the thermal reservoir and $G_{jk}(t_{2},t_{1};\tau _{2},\tau _{1})$ is an appropriate function (please refer to Refs. [26] for details). Here, it is important to note that there is no overlap between the two integrations on the right-hand side of this equation. Hence if the thermal reservoir has a sufficiently short correlation time, the correction term $\Delta \langle X_{2}(t_{2})X_{1}(t_{1})\rangle$ becomes negligibly small. In the same way, we can show that higher order correction terms are also negligible. In this case, $\mathscr {K}(t)$ becomes independent of time and $\mathscr {V}(t,t_{0})=\exp [(t-t_{0})\mathscr {K}]$ is obtained. For the system depicted in Fig. 1, we have the dynamical map $\mathscr {V}(t,t_{0})=\exp [(t-t_{0})L_{AB}]=V_{AB}(t-t_{0})$ and $W(0)=W_{A}(0)\otimes W_{B}(0)$. Thus, we can obtain Eqs. (29) and (30) from Eq. (80).