Practical covert quantum key distribution with decoy-state method

Abstract

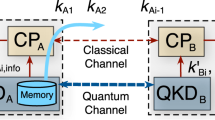
Covert communication methods are used in the communication with high security level. When it turns to quantum communication, covertness is also an important concern which is firstly discussed by Arrazola and Scarani (Phys Rev Lett, 117:250503, 2016). To make quantum key distribution (QKD) protocol more suitable in the scenarios need high security, we propose a covert QKD protocol with decoy-state method in this paper. The secure key rate and covertness of the covert decoy-state QKD are proved. We compare the performance of the covert decoy-state QKD with those of the original decoy-state QKD and covert QKD without decoy states in numerical simulations. It shows that (1) the covert decoy-state QKD can have a performance comparable to the original decoy-state QKD protocol besides its covertness; (2) the covert decoy-state QKD can have a considerable improvement of transmission distance over covert QKD without decoy states at the cost of a small change of covertness parameter. Furthermore, the statistical fluctuation due to the finite length of data is also taken into account based on the Gaussian analysis method.

Appendix

In this section, we derive Eve’s state $\sigma _\mathrm{E}$ when Alice and Bob communicate and give the details on how to obtain the bound of detection bias $\delta$.

We have

$$\begin{aligned} \sigma _\mathrm{E}=(1-q^s-q^d)\rho _\mathrm{E}+q^s\rho _s+q^d\rho _d, \end{aligned}$$

(A1)

and $\rho _\mathrm{E}$ is shown in Eq. (14). The state $\rho _s$ and $\rho _d$ can be given

$$\begin{aligned} \begin{aligned}&\rho _s=\sum _{k=0}^{2}\sum _{l=0}^{1}p(k,l)\sigma _{k,l},\\&\rho _d=\sum _{k'=0}^{2}\sum _{l'=0}^{1}p(k',l')\sigma _{k',l'}, \end{aligned} \end{aligned}$$

(A2)

where $p(k,l)=\frac{{{\bar{n}}}^k}{(1+{\bar{n}})^{k+1}}\frac{\hbox {e}^{-\mu }\mu ^l}{l!}$, $p(k',l')=\frac{{{\bar{n}}}^{k'}}{(1+{\bar{n}})^{k'+1}}\frac{\hbox {e}^{-\upsilon }\upsilon ^{l'}}{l'!}$ and $\sigma _{k,l}$ is Eve’s state when there are k photons coming from the signal states and l photons from the noise, $\sigma _{k',l'}$ is Eve’s state when there are k photons coming from the decoy states and l photons from the noise.

We can obtain

$$\begin{aligned} \rho _s&=p(0,0)\sigma _{0,0}+p(0,1)\sigma _{0,1}+p(1,0)\sigma _{1,0}+p(1,1)\sigma _{1,1} \nonumber \\&\quad +p(2,0)\sigma _{2,0}+p(2,1)\sigma _{2,1} \nonumber \\&=\Bigg [\frac{1}{1+{\bar{n}}}\hbox {e}^{-\mu }+\frac{1}{1+{\bar{n}}}\hbox {e}^{-\mu }\mu \eta +\frac{{\bar{n}}}{(1+{\bar{n}})^2}\hbox {e}^{-\mu }(1-\eta ) \nonumber \\&\quad +\frac{{\bar{n}}}{(1+{\bar{n}})^2}\hbox {e}^{-\mu }\mu 2\eta (1-\eta )+\frac{({\bar{n}})^2}{(1+{\bar{n}})^3}\hbox {e}^{-\mu }(1-\eta )^2 \nonumber \\&\quad +\frac{({\bar{n}})^2}{(1+{\bar{n}})^3}\hbox {e}^{-\mu }\mu 3\eta (1-\eta )^2\Bigg ]\left| 0\right\rangle \left\langle 0\right| \nonumber \\&\quad \quad \Bigg [\frac{1}{1+{\bar{n}}}\hbox {e}^{-\mu }\mu (1-\eta )+\frac{{\bar{n}}}{(1+{\bar{n}})^2}\hbox {e}^{-\mu }\eta +\frac{{\bar{n}}}{(1+{\bar{n}})^2}\hbox {e}^{-\mu } \nonumber \\&\quad \quad \mu (1-2\eta )^2+\frac{({\bar{n}})^2}{(1+{\bar{n}})^3}\hbox {e}^{-\mu }2\eta (1-\eta ) +\frac{({\bar{n}})^2}{(1+{\bar{n}})^3}\nonumber \\&\quad \quad \hbox {e}^{-\mu }\mu (1-\eta )(1-3\eta )^2\Bigg ]\left| 1\right\rangle \left\langle 1\right| \nonumber \\&\quad \quad \Bigg [\frac{{\bar{n}}}{(1+{\bar{n}})^2}\hbox {e}^{-\mu }\mu 2\eta (1-\eta )+\frac{({\bar{n}})^2}{(1+{\bar{n}})^3}\hbox {e}^{-\mu }\eta ^2 \nonumber \\&\quad +\frac{({\bar{n}})^2}{(1+{\bar{n}})^3}\hbox {e}^{-\mu }\mu \eta (2-3\eta )^2\Bigg ]\left| 2\right\rangle \left\langle 2\right| \nonumber \\&\quad \quad \frac{({\bar{n}})^2}{(1+{\bar{n}})^3}\hbox {e}^{-\mu }\mu 3\eta ^2(1-\eta )\left| 3\right\rangle \left\langle 3\right| . \end{aligned}$$

(A3)

In the same way, we can get the state $\rho _d$. Then Eve’s state $\sigma _\mathrm{E}$ when Alice and Bob communicate can be obtained.

The state $\rho _\mathrm{E}$ and the state $\sigma _\mathrm{E}$ that Eve gets when Alice and Bob communicate are diagonal in the Fock basis. Thus, we can treat both states as classical probability distributions and write [8]

$$\begin{aligned} D(\rho \parallel \sigma )=\sum _{n=0}^{\infty }\rho _\mathrm{E}(n)[\log (\rho _\mathrm{E}(n))-\log (\sigma _\mathrm{E}(n))], \end{aligned}$$

(A4)

where $\rho _\mathrm{E}(n)$ and $\sigma _\mathrm{E}(n)$ are the probability of observing n photons in each cases. However, higher-order terms actually decrease the value of the relative entropy. Therefore, to obtain an upper bound on the relative entropy, it suffices to consider only terms to first order in ${\bar{n}}$ and to second order in $\mu ,\upsilon$.

We can get

$$\begin{aligned} \begin{aligned} D(\rho _\mathrm{E}\parallel \sigma _\mathrm{E})&\le \rho _\mathrm{E}(0)[\log (\rho _\mathrm{E}(0))-\log (\sigma _\mathrm{E}(0))]\\&\quad +\rho _\mathrm{E}(1)[\log (\rho _\mathrm{E}(1))-\log (\sigma _\mathrm{E}(1))] \\&=\frac{\rho _\mathrm{E}(0)}{\ln 2}[\ln (\rho _\mathrm{E}(0))-\ln (\sigma _\mathrm{E}(0))]\\&\quad +\frac{\rho _\mathrm{E}(1)}{\ln 2}[\ln (\rho _\mathrm{E}(1))-\ln (\sigma _\mathrm{E}(1))]. \end{aligned} \end{aligned}$$

(A5)

We obtain a bound through a Taylor series expansion, keeping terms to second order in $\mu$.

$$\begin{aligned}&\frac{\rho _\mathrm{E}(0)}{\ln 2}\ln (\rho _\mathrm{E}(0))-\frac{\rho _\mathrm{E}(0)}{\ln 2}\ln (\sigma _\mathrm{E}(0))\le \frac{1}{\ln 2}\Bigg [\Bigg (\frac{\eta -\frac{1}{2}}{1+{\bar{n}}} \nonumber \\&\quad +\frac{{\bar{n}}(1-\eta )(2\eta -\frac{1}{2})}{(1+{\bar{n}})^2}+\frac{{\bar{n}}^2(1-\eta )^2(3\eta -\frac{1}{2})}{(1+{\bar{n}})^3}\Bigg )\mu ^2 \nonumber \\&\quad +\Bigg (\frac{1-\eta }{1+{\bar{n}}}+\frac{{\bar{n}}(1-\eta )(1-2\eta )}{(1+{\bar{n}})^2}+\frac{{\bar{n}}^2(1-\eta )^2(1-3\eta )}{(1+{\bar{n}})^3}\Bigg )\mu \nonumber \\&\quad +\frac{(1-\eta )^2}{1+{\bar{n}}}-\frac{1}{1+{\bar{n}}}-\frac{1}{(1+{\bar{n}})^2}-\frac{1}{(1+{\bar{n}})^3}\Bigg ]q^s \nonumber \\&\quad +\frac{1}{2!\ln 2\rho _\mathrm{E}(0)}\Bigg [\Bigg (\frac{\eta -1}{1+{\bar{n}}}+\frac{{\bar{n}}(1-\eta )(2\eta -1)}{(1+{\bar{n}})^2} \nonumber \\&\quad +\frac{{\bar{n}}^2(1-\eta )^2(3\eta -1)}{(1+{\bar{n}})^3}\Bigg )^2\mu ^2+2\Bigg (\frac{\frac{1}{2}-\eta }{1+{\bar{n}}}+\frac{{\bar{n}}(1-\eta )(\frac{1}{2}-2\eta )}{(1+{\bar{n}})^2} \nonumber \\&\quad \quad \frac{{\bar{n}}^2(1-\eta )^2(\frac{1}{2}-3\eta )}{(1+{\bar{n}})^3}\Bigg )\Bigg (\frac{1}{1+{\bar{n}}}+\frac{1}{(1+{\bar{n}})^2}+\frac{1}{(1+{\bar{n}})^3} \nonumber \\&\quad -\frac{(1-\eta )^2}{1+{\bar{n}}}\Bigg )\mu ^2+2\Bigg (\frac{\eta -1}{1+{\bar{n}}}+\frac{{\bar{n}}(1-\eta )(2\eta -1)}{(1+{\bar{n}})^2} \nonumber \\&\quad +\frac{{\bar{n}}^2(1-\eta )^2(3\eta -1)}{(1+{\bar{n}})^3}\Bigg )\Bigg (\frac{1}{1+{\bar{n}}}+\frac{1}{(1+{\bar{n}})^2}+\frac{1}{(1+{\bar{n}})^3} \nonumber \\&\quad -\frac{(1-\eta )^2}{1+{\bar{n}}}\Bigg )\mu +\Bigg (\frac{1}{1+{\bar{n}}}+\frac{1}{(1+{\bar{n}})^2}+\frac{1}{(1+{\bar{n}})^3} \nonumber \\&\quad -\frac{(1-\eta )^2}{1+{\bar{n}}}\Bigg )^2\Bigg ](q^s)^2, \end{aligned}$$

(A6)

and

$$\begin{aligned}&\frac{\rho _\mathrm{E}(1)}{\ln 2}\ln (\rho _\mathrm{E}(1))-\frac{\rho _\mathrm{E}(1)}{\ln 2}\ln (\sigma _\mathrm{E}(1)) \nonumber \\&\le \frac{1}{\ln 2}\Bigg [\Bigg (\frac{1-\eta }{1+{\bar{n}}} +\frac{{\bar{n}}(1-2\eta )^2}{(1+{\bar{n}})^2}-\frac{\frac{1}{2}{\bar{n}}\eta }{(1+{\bar{n}})^2}+\frac{{\bar{n}}^2(1-\eta )(1-3\eta )^2}{(1+{\bar{n}})^3} \nonumber \\&\quad -\frac{\frac{1}{2}{\bar{n}}^22\eta (1-\eta )}{(1+{\bar{n}})^3}\Bigg )\mu ^2+\Bigg (-\frac{1-\eta }{1+{\bar{n}}}+\frac{{\bar{n}}\eta }{(1+{\bar{n}})^2} \nonumber \\&\quad -\frac{{\bar{n}}(1-2\eta )^2}{(1+{\bar{n}})^2}+\frac{{\bar{n}}^22\eta (1-\eta )^2}{(1+{\bar{n}})^3}-\frac{{\bar{n}}^2(1-\eta )(1-3\eta )^2}{(1+{\bar{n}})^3}\Bigg )\mu \nonumber \\&\quad +\frac{{\bar{n}}^2(1-\eta )^2}{(1+{\bar{n}})^4}-\frac{{\bar{n}}\eta }{(1+{\bar{n}})^2}-\frac{{\bar{n}}^22\eta (1-\eta )}{(1+{\bar{n}})^3}\Bigg ]q^s \nonumber \\&\quad +\frac{1}{2!\ln 2\rho _\mathrm{E}(1)}\Bigg [\Bigg (\frac{1-\eta }{1+{\bar{n}}}-\frac{{\bar{n}}\eta }{(1+{\bar{n}})^2}+\frac{{\bar{n}}(1-2\eta )^2}{(1+{\bar{n}})^2} \nonumber \\&\quad +\frac{{\bar{n}}^22\eta (1-\eta )}{(1+{\bar{n}})^3}-\frac{{\bar{n}}^2(1-\eta )(1-3\eta )^2}{(1+{\bar{n}})^3}\Bigg )^2\mu ^2 \nonumber \\&\quad +2\Bigg (-\frac{1-\eta }{1+{\bar{n}}}+\frac{\frac{1}{2}{\bar{n}}\eta }{(1+{\bar{n}})^2}-\frac{{\bar{n}}(1-2\eta )^2}{(1+{\bar{n}})^2}-\frac{\frac{1}{2}{\bar{n}}^22\eta (1-\eta )}{(1+{\bar{n}})^3} \nonumber \\&\quad +\frac{{\bar{n}}^2(1-\eta )(1-3\eta )^2}{(1+{\bar{n}})^3}\Bigg )\Bigg (\frac{{\bar{n}}\eta }{(1+{\bar{n}})^2}+\frac{{\bar{n}}^22\eta (1-\eta )}{(1+{\bar{n}})^3} \nonumber \\&\quad -\frac{{\bar{n}}^2(1-\eta )^2}{(1+{\bar{n}})^4}\Bigg )\mu ^2+2\Bigg (\frac{1-\eta }{1+{\bar{n}}}-\frac{{\bar{n}}\eta }{(1+{\bar{n}})^2}+\frac{{\bar{n}}(1-2\eta )^2}{(1+{\bar{n}})^2} \nonumber \\&\quad -\frac{{\bar{n}}^22\eta (1-\eta )}{(1+{\bar{n}})^3}+\frac{{\bar{n}}^2(1-\eta )(1-3\eta )^2}{(1+{\bar{n}})^3}\Bigg )\Bigg (\frac{{\bar{n}}\eta }{(1+{\bar{n}})^2} \nonumber \\&\quad +\frac{{\bar{n}}^22\eta (1-\eta )}{(1+{\bar{n}})^3}-\frac{{\bar{n}}^2(1-\eta )^2}{(1+{\bar{n}})^4}\Bigg )\mu +\Bigg (\frac{{\bar{n}}\eta }{(1+{\bar{n}})^2} \nonumber \\&\quad +\frac{{\bar{n}}^22\eta (1-\eta )}{(1+{\bar{n}})^3}-\frac{{\bar{n}}^2(1-\eta )^2}{(1+{\bar{n}})^4}\Bigg )^2\Bigg ](q^s)^2. \end{aligned}$$

(A7)

According to these two bounds, and in the same way, keeping terms to second order in $\upsilon$, we can obtain an upper bound on the relative entropy,

$$\begin{aligned} \begin{aligned}&D(\rho _\mathrm{E}\parallel \sigma _\mathrm{E}) \\&\quad \le \frac{1}{\ln 2}\Bigg [\frac{{\bar{n}}^3+4{\bar{n}}^2}{(1+{\bar{n}})^4}+\frac{2{\bar{n}}\mu }{(1+{\bar{n}})^2}+\frac{(2{\bar{n}}+1)\mu ^2}{2(1+{\bar{n}})^2}\Bigg ]q^s \\&\qquad +\frac{1}{\ln 2}\Bigg [\frac{{\bar{n}}^2+{\bar{n}}+2}{(1+{\bar{n}})^2}+\frac{10{\bar{n}}^4+23{\bar{n}}^3+14{\bar{n}}^2}{(1+{\bar{n}})^4}\mu \\&\qquad +\frac{6{\bar{n}}^3+9{\bar{n}}^2+5{\bar{n}}}{(1+{\bar{n}})^3}\mu ^2\Bigg ](q^s)^2+\frac{1}{\ln 2}\Bigg [\frac{{\bar{n}}^3+4{\bar{n}}^2}{(1+{\bar{n}})^4}+\frac{2{\bar{n}}\upsilon }{(1+{\bar{n}})^2} \\&\qquad +\frac{(2{\bar{n}}+1)\upsilon ^2}{2(1+{\bar{n}})^2}\Bigg ]q^d+\frac{1}{\ln 2}\Bigg [\frac{{\bar{n}}^2+{\bar{n}}+2}{(1+{\bar{n}})^2} \\&\qquad +\frac{10{\bar{n}}^4+23{\bar{n}}^3+14{\bar{n}}^2}{(1+{\bar{n}})^4}\upsilon +\frac{6{\bar{n}}^3+9{\bar{n}}^2+5{\bar{n}}}{(1+{\bar{n}})^3}\upsilon ^2\Bigg ](q^d)^2. \end{aligned} \end{aligned}$$

(A8)

Thus, using

$$\begin{aligned} \delta \le \sqrt{\frac{1}{8}D(\rho \parallel \sigma )}=\sqrt{\frac{N}{8}D(\rho _\mathrm{E}\parallel \sigma _\mathrm{E})}, \end{aligned}$$

(A9)

the detection bias $\delta$ finally can be bounded as

$$\begin{aligned} \begin{aligned} \delta&\le \Bigg [\Bigg (\frac{{\bar{n}}^3+4{\bar{n}}^2}{\mu (1+{\bar{n}})^4}+\frac{2{\bar{n}}}{(1+{\bar{n}})^2}+\frac{(2{\bar{n}}+1)\mu }{2(1+{\bar{n}})^2}\Bigg )\frac{N^s}{8\ln 2} \\&\quad +\Bigg (\frac{{\bar{n}}^3+4{\bar{n}}^2}{\upsilon (1+{\bar{n}})^4}+\frac{2{\bar{n}}}{(1+{\bar{n}})^2}+\frac{(2{\bar{n}}+1)\upsilon }{2(1+{\bar{n}})^2}\Bigg )\frac{N^d}{8\ln 2} \\&\quad +\Bigg (\frac{{\bar{n}}^2+{\bar{n}}+2}{\mu ^2(1+{\bar{n}})^2}+\frac{10{\bar{n}}^4+23{\bar{n}}^3+14{\bar{n}}^2}{\mu (1+{\bar{n}})^4} \\&\quad +\frac{6{\bar{n}}^3+9{\bar{n}}^2+5{\bar{n}}}{(1+{\bar{n}})^3}\Bigg )\frac{(N^s)^2}{8N\ln 2}+\Bigg (\frac{{\bar{n}}^2+{\bar{n}}+2}{\upsilon ^2(1+{\bar{n}})^2} \\&\quad +\frac{10{\bar{n}}^4+23{\bar{n}}^3+14{\bar{n}}^2}{\upsilon (1+{\bar{n}})^4}+\frac{6{\bar{n}}^3+9{\bar{n}}^2+5{\bar{n}}}{(1+{\bar{n}})^3}\Bigg )\frac{(N^d)^2}{8N\ln 2}\Bigg ]^{\frac{1}{2}}, \end{aligned} \end{aligned}$$

(A10)

where $N^s$ and $N^d$, respectively, denote the signal states and decoy states sent by Alice.