Plug-and-play unidimensional continuous-variable quantum key distribution

Abstract

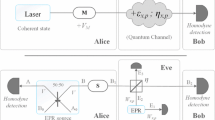
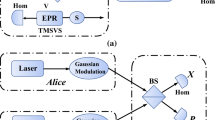
Numerous continuous-variable quantum key distribution (CV-QKD) schemes are based on the Gaussian modulation, which is carried out in conjugate quadratures. In order to simplify the traditional protocols, as well as improving the security of the system, we propose the plug-and-play unidimensional CV-QKD protocol, which waives the necessity of propagating a local oscillator (LO) between legitimate users and generates a real local LO for quantum measurement. The new protocol utilizes only one phase modulator rather than two, which is different from the dual-phase-modulated coherent-states protocol that we proposed earlier. The prepare-and-measure and entanglement-based schemes are described. The security of the new protocol against collective attacks in a Gaussian channel is analyzed, and the security boundary is derived, which is achieved by establishing the relationship between the uncertain parameters of the unmodulated quadrature. The performance of it is analyzed in both asymptotic and finite-size cases. Such an efficient scheme not only provides a way of removing the security loopholes associated with the transmitting LO, but also eliminates the need for one of the phase modulators, and thus will facilitate commercialization of continuous-variable quantum key distribution.

Appendices

Appendix A: The derivation of the symplectic eigenvalues

To calculate the second part of (17), we need to calculate the symplectic eigenvalues of the covariance matrix $\gamma _{BHG}^{p_A}$, which can be characterized by the following equation:

$$\begin{aligned} \gamma _{BHG}^{p_A}=\gamma _{BHG}-\sigma _{BHGA}^T(X \gamma _A X)^{MP}\sigma _{BHGA}, \end{aligned}$$

(34)

where $\gamma _{BHG}$, $\gamma _A$, and $\sigma _{BHGA}$ are the submatrix of $\gamma _{BHGA}$, and

$$\begin{aligned} \gamma _{BHGA}=\begin{bmatrix} \gamma _{BHG}&\sigma _{BHGA} \\ \sigma _{BHGA}^T&\gamma _A \end{bmatrix}, \end{aligned}$$

(35)

which can be derived by rearranging the lines and columns of matrix $\gamma _{BAHG}$ describing the state $\rho _{BAHG}$. Specifically, $\gamma _{BAHG}$ can be derived by applying a beam splitter transformation $Y^{AS}$ that models the inefficiency of the detector and acts on modes $A_2$ and $H_0$ [52], and it is given as follows:

$$\begin{aligned} \gamma _{BHGA}=(Y^{AS})^T[\gamma _{BA_2}\oplus \gamma _{H_0 G}]Y^{AS}, \end{aligned}$$

(36)

where $Y^{AS}=\varPi _B \oplus Y_{A_2 H_0}^{AS} \oplus \varPi _G$, with

$$\begin{aligned} Y_{A_2 H_0}^{AS}=\begin{bmatrix} \sqrt{\eta } \cdot \varPi _2&\sqrt{1-\eta } \cdot \varPi _2 \\ -\sqrt{1-\eta } \cdot \varPi _2&\sqrt{\eta } \cdot \varPi _2 \end{bmatrix}, \end{aligned}$$

(37)

$\gamma _{H_0 G}$ is the matrix that describes the EPR state of variance $V_d$ used to model the detector’s electronic noise, and it is written as

$$\begin{aligned} \gamma _{H_0 G}=\begin{bmatrix} V_d \cdot \varPi _2&\sqrt{V_d^2-1} \cdot \sigma _z \\ \sqrt{V_d^2-1} \cdot \sigma _z&V_d \cdot \varPi _2 \end{bmatrix}. \end{aligned}$$

(38)

Therefore, we can calculate the symplectic eigenvalues of the covariance matrix $\gamma _{BHG}^{p_A}$:

$$\begin{aligned} \lambda _{3,4}^2=\frac{1}{2}\left( C \pm \sqrt{C^2-4D}\right) ,\lambda _5=1, \end{aligned}$$

(39)

where

$$\begin{aligned} C= & {} \frac{A(1+v_{el})+((\varepsilon _p T_p+1)(V^2+1)+(V^2-1) T_p-A)\eta }{1+\varepsilon _p T_p \eta +(V^2-1)T_p \eta +v_{el}}, \nonumber \\ D= & {} \frac{B(1+v_{el}-\eta )+V^2 (1+\varepsilon _p T_p)\eta }{1+\varepsilon _p T_p \eta +(V^2-1) T_p \eta +v_{el}}. \end{aligned}$$

(40)

Appendix B: Physical constraint

This Eq. (25) imposes physical constraints on the possible values of $C_x^{A_2}$ and $V_x^{A_2}$. Such constraint can be further described by the following parabolic inequality:

$$\begin{aligned} (C_x^{A_2})^2 \le \frac{V^2-1}{V} ((1-T_p V_0)V_x^{A_2} + V_0), \end{aligned}$$

(41)

where $V_0 = \frac{1}{1+T_p (\xi _p^2+2V\xi _p+\varepsilon _p)}$.

Considering that $C_x^{A_2}=\sqrt{\frac{T_x (V^2-1)}{V}}, V_x^{A_2}=1+T_x \varepsilon _x$, the above parabolic inequality transforms into the following inverse function inequality:

$$\begin{aligned} \varepsilon _x \ge \frac{V_0 (T_p-1)-1}{1-T_p V_0} \cdot \frac{1}{T_x}+\frac{1}{1-T_p V_0}. \end{aligned}$$

(42)

From the mathematical relationship, we can know that the inverse function inequality is satisfied if $\varepsilon _x \ge 0$ and $T_x \in [0, 1]$. Therefore, Eq. (25) is true in the same condition. It means that the plug-and-play UD protocol always satisfies the requirement of the physicality of the state.