The study of interference effect in a globally coupled quantum network

Abstract

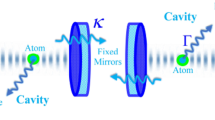
We investigate the quantum interference effect in a globally coupled quantum network that is composed of N lowly dissipative optical cavities and a highly dissipative cavity. After effectively eliminating the highly dissipative mode, we obtain the effective master equation including some additional terms. In particular, these additional terms can explain the interference effect between any two different coupling paths of the quantum network. To demonstrate the practical application of the interference effect, we consider the manipulation of heat flows as an example. The results show that the heat currents can be effectively dominated by adjusting interference angles and amplitudes, and thus the function of some thermal devices can be achieved, such as the thermal diode, thermal switch, and thermal modulator.

Appendix

To derive the effective master equation, utilizing the frequency conduction $\omega _j=2\omega$, we first transform the master equation to the interaction picture by applying a unitary operator

$$\begin{aligned} {\hat{U}}(t)=\exp \left\{ -i\left( \sum ^N_{j=1}\omega _j{\hat{a}}^{\dagger }_j{\hat{a}}_j+\omega {\hat{b}}^{\dagger }{\hat{b}}\right) t\right\} , \end{aligned}$$

(1)

and then the master equation in the interaction picture can be expressed as

$$\begin{aligned} \frac{\mathrm{d}{\hat{\rho }}_I(t)}{\mathrm{d}t}=\left( {\mathcal {L}}_{I}+{\mathcal {L}}_0 +\sum ^N_{j=1}{\mathcal {L}}_{j}\right) {\hat{\rho }}_I(t), \end{aligned}$$

(2)

where density operator $\rho _I(t)={\hat{U}}^{\dagger }\rho (t){\hat{U}}$ and the Liouvillian superoperator

$$\begin{aligned} {\mathcal {L}}_I=-i\left[ \left( \sum ^{N}_{i,j}\frac{J_{ij}}{2}{\hat{a}}^{\dagger }_i{\hat{a}}_j+ \sum ^N_{j=1} g_j{\hat{a}}_j{\hat{b}}^{\dagger 2}\right) +h.c.,\varvec{\cdot }\right] . \end{aligned}$$

(3)

In Eq. (2), ${\mathcal {L}}_0$ is the dominant decay tunnel of the system which is created by the reservoir of the highly dissipative cavity. Hence, a reduced master equation can be obtained by eliminating the highly dissipative cavity mode and the method has been mentioned in [40,41,42] which is a commonly used technique to estimate the highly dissipative cavity mode and obtain the effective master equation. Accordingly, we make a transformation for the density operator $\rho _I(t)$, i.e.,

$$\begin{aligned} \rho '_I(t)=\exp \left\{ -\left( {\mathcal {L}}_0+\sum ^N_{j=1}{\mathcal {L}}_{j}\right) t\right\} \rho _I(t). \end{aligned}$$

(4)

The dynamical evolution equation of Eq. (4) is expressed as

$$\begin{aligned} \frac{\mathrm{d}\rho '_I(t)}{\mathrm{d}t}=\mathcal {L'}_I\rho '_I(t), \end{aligned}$$

(5)

where

$$\begin{aligned} {\mathcal {L}}'_I=\exp \left\{ -\left( {\mathcal {L}}_0 +\sum ^N_{j=1}{\mathcal {L}}_{j}\right) t\right\} {\mathcal {L}}_I\exp \left\{ \left( {\mathcal {L}}_0 +\sum ^N_{j=1}{\mathcal {L}}_{j}\right) t\right\} . \end{aligned}$$

(6)

In Eq. (6), ${\mathcal {L}}_{0}$ and ${\mathcal {L}}_{j}$ are different decay channels that are described by different degrees of freedom of the system, so all the Lindblad superoperators are commutative to each other, i.e., $[{\mathcal {L}}_{i},{\mathcal {L}}_{j}]=0$, and $[{\mathcal {L}}_{i},{\mathcal {L}}_0]=0$, with $i,j=1,2\ldots ,N$. According to these commutation relations, we can expand ${\mathcal {L}}'_I$ as

$$\begin{aligned} \begin{aligned} {\mathcal {L}}'_I=&-i\big [({\mathcal {A}}_1{\mathcal {B}}_1+{\mathcal {A}}_2{\mathcal {B}}_2-{\mathcal {A}}^{\dagger }_1{\mathcal {B}}^{\dagger }_1 -{\mathcal {A}}^{\dagger }_2{\mathcal {B}}^{\dagger }_2+{\mathcal {O}}-{\mathcal {O}}^{\dagger }\big ], \end{aligned} \end{aligned}$$

(7)

where the superoperators describing the lowly and highly dissipative modes can be expanded by the superoperators of the original frame, that is,

$$\begin{aligned} \begin{aligned} {\mathcal {A}}_1=&\exp \left\{ -\sum ^N_{j=1}{\mathcal {L}}_{j}t\right\} \left( \sum ^N_{j=1} g_j({\hat{a}}_j\varvec{\cdot })\right) \exp \left\{ \sum ^N_{j=1}{\mathcal {L}}_jt\right\} ,\\ {\mathcal {A}}_2=&\exp \left\{ -\sum ^N_{j=1}{\mathcal {L}}_jt\right\} \left( \sum ^N_{j=1} g^*_j({\hat{a}}^{\dagger }_j\varvec{\cdot })\right) \exp \left\{ \sum ^N_{j=1}{\mathcal {L}}_jt\right\} , \\ {\mathcal {B}}_1=&e^{-{\mathcal {L}}_0t}({\hat{b}}^{\dagger 2}\varvec{\cdot })e^{{\mathcal {L}}_0t}, \\ {\mathcal {B}}_2=&e^{-{\mathcal {L}}_0t}({\hat{b}}^2\varvec{\cdot })e^{{\mathcal {L}}_0t}, \\ {\mathcal {B}}_3=&e^{-{\mathcal {L}}_0t}({\hat{b}}^{\dagger }\varvec{\cdot }{\hat{b}}^{\dagger })e^{{\mathcal {L}}_0t}, \end{aligned} \end{aligned}$$

(8)

and the superoperator describing the linear interactions between the highly dissipative cavities is

$$\begin{aligned} \begin{aligned} {\mathcal {O}}=&\exp \left\{ -\sum ^N_{j=1} {\mathcal {L}}_jt\right\} \left( \sum ^N_{i\ne j}J_{ij}({\hat{a}}^{\dagger }_i{\hat{a}}_j \varvec{\cdot })\right) \exp \left\{ \sum ^N_{j=1}{\mathcal {L}}_{j}t\right\} . \end{aligned} \end{aligned}$$

(9)

From Eqs. (8) and (9), we know that all the superoperators are time dependent. In order to expand the ${\mathcal {B}}_i (i=1,2,3)$ with time-independent superoperators, we need to investigate the corresponding dynamical evolution equation. After some calculation, we obtain the corresponding dynamical evolution equation which has the similar form with the Liouvillian equation

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}{\mathcal {B}}_i=[{\mathcal {B}}_i,{\mathcal {L}}_0] =[{\mathcal {B}}_i,{\mathcal {L}}'_0], \end{aligned}$$

(10)

where we have used the relation ${\mathcal {L}}_0={\mathcal {L}}'_0$. Besides, by constructing a vector ${\mathcal {B}}(t)=({\mathcal {B}}_1,{\mathcal {B}}^{\dagger }_2,{\mathcal {B}}_3)^T$ and combining Eq. (10), we obtain a set of differential equations of the first order

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\mathbf {{\mathcal {B}}}(t)=M\mathbf {{\mathcal {B}}}(t), \end{aligned}$$

(11)

and the coefficient matrix is

$$\begin{aligned} M=\left[ \begin{array}{ccc} \kappa (2{\bar{n}}+1) &{} 0 &{} -2\kappa ({\bar{n}}+1) \\ 0 &{} -\kappa (2{\bar{n}}+1) &{} 2\kappa {\bar{n}} \\ \kappa {\bar{n}} &{} -\kappa ({\bar{n}}+1) &{} 0 \end{array} \right] \end{aligned}$$

(12)

The solution of Eq. (12) can be obtained strictly

$$\begin{aligned} \mathbf {{\mathcal {B}}}(t)=e^{Mt}\mathbf {{\mathcal {B}}}(0)\equiv S(t)\mathbf {{\mathcal {B}}}(0), \end{aligned}$$

(13)

where the initial value is $\mathbf {{\mathcal {B}}}(0)=(({\hat{b}}^{\dagger 2}\varvec{\cdot }),({\hat{b}}^{\dagger }\varvec{\cdot }{\hat{b}}^{\dagger }),(\varvec{\cdot }{\hat{b}}^{\dagger 2}))^T$ and S(t) is a real matrix. ${\mathcal {B}}_i$ can be represented by its initial value and the matrix element of S(t), that is,

$$\begin{aligned} \begin{aligned} {\mathcal {B}}_1=&S_{11}(t){\mathcal {B}}_1(0)+S_{12}(t){\mathcal {B}}^{\dagger }_{2}(0)+S_{13}(t){\mathcal {B}}_3(0), \\ {\mathcal {B}}_2=&S_{21}(t){\mathcal {B}}^{\dagger }_1(0)+S_{22}(t){\mathcal {B}}_{2}(0)+S_{23}(t){\mathcal {B}}^{\dagger }_3(0), \\ {\mathcal {B}}_3=&S_{31}(t){\mathcal {B}}_1(0)+S_{32}(t){\mathcal {B}}^{\dagger }_{2}(0)+S_{33}(t){\mathcal {B}}_3(0), \end{aligned} \end{aligned}$$

(14)

where the parameters related to the highly dissipative tunnel are included in the matrix element of S(t). In order to expand and simplify the superoperator ${\mathcal {L}}'_I$, we plug the vector of Eq. (14) into Eq. (7) and then obtain the corresponding expression

$$\begin{aligned} \begin{aligned} {\mathcal {L}}'_I=&-i\big [(S_{11}(t){\mathcal {A}}_1(t)-S_{21}(t){\mathcal {A}}^{\dagger }_2(t))(b^{\dagger 2}\varvec{\cdot }) +(S_{12}(t){\mathcal {A}}_1(t)\\&-S_{22}(t){\mathcal {A}}^{\dagger }_2(t))(\varvec{\cdot }b^{\dagger 2}) +(S_{13}(t){\mathcal {A}}_1(t)-S_{23}(t){\mathcal {A}}^{\dagger }_2(t))(b^{\dagger }\varvec{\cdot }b^{\dagger })\\&+(S_{21}(t){\mathcal {A}}_2(t)-S_{11}(t){\mathcal {A}}^{\dagger }_1(t))(\varvec{\cdot }b^2) + (S_{22}(t){\mathcal {A}}_2(t)\\&-S_{12}(t){\mathcal {A}}^{\dagger }_1(t))(b^2\varvec{\cdot }) +(S_{23}(t){\mathcal {A}}_2(t)-S_{13}(t){\mathcal {A}}^{\dagger }_1(t))(b\varvec{\cdot }b)\\&+{\mathcal {O}}(t)-{\mathcal {O}}^{\dagger }(t) \big ]. \end{aligned} \end{aligned}$$

(15)

We formally integrate Eq. (5), and then the calculation result can be written as

$$\begin{aligned} {\hat{\rho }}'_I(t)={\hat{\rho }}'_I(0)+\int ^{t}_0\mathrm{d}\tau {\mathcal {L}}'_I(\tau ){\hat{\rho }}'_I(\tau ). \end{aligned}$$

(16)

Moreover, plugging Eq. (16) into Eq. (3), we can obtain the following dynamic equation

$$\begin{aligned} \frac{\mathrm{d}{\hat{\rho }}'_I(t)}{\mathrm{d}t}={\mathcal {L}}'_I(t){\hat{\rho }}'_I(0) +\int ^t_0\mathrm{d}\tau {\mathcal {L}}'_I(t){\mathcal {L}}'_I(\tau ){\hat{\rho }}'_I(\tau ). \end{aligned}$$

(17)

By partially tracing the highly dissipative cavity mode for Eq. (17), we obtain the dynamic evolution of the reduced density operator

$$\begin{aligned} \frac{\mathrm{d}{\hat{\rho }}''_{I}(t)}{\mathrm{d}t}={\text {Tr}}_b\left\{ {\mathcal {L}}'_I(t) \left( {\hat{\rho }}'_I(0)+\int ^t_0\mathrm{d}\tau {\mathcal {L}}'_I(\tau ){\hat{\rho }}'_I(\tau )\right) \right\} , \end{aligned}$$

(18)

where ${\hat{\rho }}''_I(t)={\text {Tr}}_b{\lbrace {\hat{\rho }}'_I(t)\rbrace }$ is the reduced density operator of the system. For our model, the highly dissipative cavity reaches the thermal state on a scale of $1/\kappa$ that is extremely short. Besides, coupling strengths between the lowly dissipative cavities and the highly dissipative cavity are weak. Hence, under these conditions, the density operator in the initial frame can be represented as a product state, i.e.,

$$\begin{aligned} {\hat{\rho }}(t)\approx {\hat{\rho }}_{a}(t)\otimes \rho _b(t), \end{aligned}$$

(19)

where ${\hat{\rho }}_a$ is the reduced density operator describing all the lowly dissipative cavity modes and ${\hat{\rho }}_b$ is the reduced density operator for the highly dissipative cavity mode. The dynamics of the system can be approximately represented by ${\hat{\rho }}_a$ when the time scale is slower than $1/\kappa$. During to the rapid dissipation of the highly dissipative cavity, the state ${\hat{\rho }}_b$ coincides with the state of its reservoirs, that is a thermal equilibrium state

$$\begin{aligned} {\hat{\rho }}_a(t)=\sum ^{\infty }_{n=0}\frac{{\bar{n}}^{n}}{(1+{\bar{n}})^{n+1}}\vert n\rangle \langle n\vert \end{aligned}$$

(20)

where $\vert n\rangle$ is the basis of the Fock space and ${\bar{n}}$ is the mean photon number of the cavity. According to the characteristics of the thermal state, i.e., ${\text {Tr}}{({\hat{b}}^2{\hat{\rho }}_b)}={\text {Tr}}{({\hat{b}}^{\dagger 2}{\hat{\rho }}_b)}=0$, the first term of Eq. (18) can be simplified as

$$\begin{aligned} {\text {Tr}}_b{({\mathcal {L}}'_I(t){\hat{\rho }}'_I(0))}=-i\big [{\mathcal {O}}(t) -{\mathcal {O}}^{\dagger }(t)\big ]{\hat{\rho }}''_I(t). \end{aligned}$$

(21)

Similarly, according to ${\text {Tr}}{({\hat{b}}^2{\hat{\rho }}_b)}={\text {Tr}}{({\hat{b}}^{\dagger 2}{\hat{\rho }}_b)}=0$, the cross-product between superoperators ${\mathcal {O}}$ and ${\mathcal {B}}_i (i=1,2,3)$ has zero trace. Moreover, $J^2_{ij}\ll 2{\bar{n}}^2\vert g_i\vert \vert g_j\vert /\kappa ,$ with $i,j=1,2,\ldots , N$, the product between superoperators ${\mathcal {O}}(t)$ and ${\mathcal {O}}(\tau )$ is very small and therefore we can ignore this term in the second term of Eq. (18). Applying the relation ${\text {Tr}}{({\hat{b}}^{\dagger 2}{\hat{b}}^2{\hat{\rho }}_b)}=2{\bar{n}}^2$ and ${\text {Tr}}{({\hat{b}}^{\dagger }{\hat{b}}{\hat{\rho }}_b)}={\bar{n}}$, we can expand the second term of Eq. (18) to

$$\begin{aligned} \begin{aligned} \int _{0}^t \mathrm{d}\tau {\text {Tr}}_b{\big \lbrace {\mathcal {L}}'_I(t){\mathcal {L}}'_I(\tau ) {\hat{\rho }}'_I(\tau )\big \rbrace }=&\int ^t_0 \mathrm{d}\tau e^{-\kappa (t-\tau )}\Big \lbrace 2{\bar{n}}^2\Big ({\mathcal {A}}_2(t){\mathcal {A}}^{\dagger }_2(\tau )\\&-{\mathcal {A}}_1(t){\mathcal {A}}_2(\tau ) +{\mathcal {A}}^{\dagger }_2(t) {\mathcal {A}}_2(\tau ) \\&-{\mathcal {A}}^{\dagger }_1(t){\mathcal {A}}^{\dagger }_2(\tau )\Big ) +2({\bar{n}}+1)^2\\&\Big ({\mathcal {A}}_1(t){\mathcal {A}}^{\dagger }_1(\tau ) -{\mathcal {A}}_2(t){\mathcal {A}}_1(\tau )\\&+{\mathcal {A}}^{\dagger }_1(t){\mathcal {A}}_1(\tau )-{\mathcal {A}}^{\dagger }_2(t) {\mathcal {A}}^{\dagger }_1(\tau )\Big ) \Big \rbrace \end{aligned} \end{aligned}$$

(22)

As we mentioned earlier, the dynamics of the quantum transmission network are slower than a time scale $1/\kappa$, i.e., the exponential function in the time Eq. (22) decays rapidly. It can also be explained by using the language of mathematics that the exponential function tends to a delta function [41]

$$\begin{aligned} e^{-\kappa (t-\tau )}\longrightarrow \frac{2}{\kappa }\delta (t-\tau ). \end{aligned}$$

(23)

This limit is equivalent to the Markovian approximation in an open quantum system that ignores the memory effects of the highly dissipative cavity mode. Applying the relation Eq. (23) to expand and simplify Eq. (22), we can obtain the dynamical evolution equation of ${\hat{\rho }}''_I(t)$, i.e.,

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}\rho ''_{I}(t)}{\mathrm{d}t}=&\exp \left\{ -\sum ^N_{j=1}{\mathcal {L}}_jt \right\} \left\{ \frac{4{\bar{n}}^2}{\kappa }\left\{ \sum ^N_{j=1}\vert g_j\vert ^2\left[ 2({\hat{a}}^{\dagger }_j\varvec{\cdot }{\hat{a}}_j) -({\hat{a}}_j{\hat{a}}^{\dagger }_j\varvec{\cdot }) -(\varvec{\cdot }{\hat{a}}_j{\hat{a}}^{\dagger }_j) \right] \right. \right. \\&\left. \left. +\sum ^N_{i\ne j}g^*_ig_j\left[ 2({\hat{a}}^{\dagger }_i\varvec{\cdot }{\hat{a}}_j) -({\hat{a}}_j{\hat{a}}^{\dagger }_i\varvec{\cdot }) \rbrace -(\varvec{\cdot }{\hat{a}}_j{\hat{a}}^{\dagger }_i)\right] \right. \right. \\&\left. \left. + \frac{4({\bar{n}}+1)^2}{\kappa }\left\{ \sum ^N_j\vert g_j\vert ^2\left[ 2({\hat{a}}_j\varvec{\cdot }{\hat{a}}^{\dagger }_j) -({\hat{a}}^{\dagger }_j{\hat{a}}_j\varvec{\cdot }) -(\varvec{\cdot }{\hat{a}}^{\dagger }_j{\hat{a}}_j) \right] \right. \right. \right. \\&\left. \left. \left. +\sum ^N_{i\ne j}g_ig^*_j\left[ 2({\hat{a}}_i\varvec{\cdot }{\hat{a}}^{\dagger }_j) -({\hat{a}}^{\dagger }_j{\hat{a}}_i\varvec{\cdot }) -(\varvec{\cdot }{\hat{a}}^{\dagger }_j{\hat{a}}_i)\right] \right\} -i\left\{ \sum ^N_{i\ne j}\frac{J_{ij}}{2}[({\hat{a}}^{\dagger }_i{\hat{a}}_j\varvec{\cdot })\right. \right. \right. \\&\left. \left. +({\hat{a}}^{\dagger }_j{\hat{a}}_i\varvec{\cdot })- (\varvec{\cdot }{\hat{a}}^{\dagger }_i{\hat{a}}_j)-(\varvec{\cdot }{\hat{a}}^{\dagger }_j {\hat{a}}_i]\right\} \right\} \exp \left\{ \sum ^N_{j=1}{\mathcal {L}}_jt\right\} \rho ''_{I}(t). \end{aligned} \end{aligned}$$

(24)

Next, we transform the master equation Eq. (24) back to the original frame by an operation

$$\begin{aligned} {\hat{\rho }}_a={\hat{U}}\exp \left\{ \sum ^N_{j=1}{\mathcal {L}}_jt\right\} \rho ''_{I}(t) {\hat{U}}^{\dagger }. \end{aligned}$$

(25)

Differentiating Eq. (25) with respect to time, and together with Eqs. (1) and (24), we can obtain the effective master equation (6).