Skip to main content

Advertisement

Springer Nature Link
Log in

A new kind of universal and flexible quantum information splitting scheme with multi-coin quantum walks

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

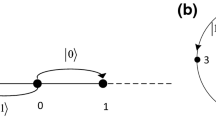
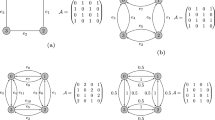
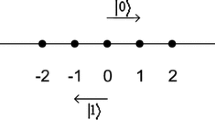
Quantum walks have received much attention due to their many potential applications for quantum information processing in recent years. In this paper, we propose a novel class of universal and flexible quantum information splitting scheme of an arbitrary qubit and d-dimensional qudit via using the model of quantum walks with multiple coins for the first time. Firstly, for splitting an arbitrary qubit into N parts, quantum walks on the line with \(N+1\) coins, which are homogeneous and position dependent, are used, respectively. In addition, it can be generalized to the model of quantum walks on the cycle for fulfilling this scheme. Secondly, for distributing an unknown d-dimensional qudit into N parts, quantum walks with \(N+1\) coins are used on the complete graph and the d-regular graph, respectively. Our scheme has two significant merits: (i) It is universal and flexible, which implies that based on the different quantum walks structures, not only an unknown qubit but also d-dimensional qudit can be shared; (ii) the prior entangled state is not necessarily prepared and the entanglement measurement is not needed, which make this scheme more convenient for the agents in applications on a network. This work opens wider application purpose of quantum walks and provides inspiration to explore the potential applications of quantum walks.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Aharonov, Y., Davidovich, L., Zagury, N.: Quantum random walks. Phys. Rev. A 48(2), 1687 (1993)

    Article  ADS  Google Scholar 

  2. Shenvi, N., Kempe, J., Whaley, K.B.: Quantum random-walk search algorithm. Phys. Rev. A 67(5), 052307 (2003)

    Article  ADS  Google Scholar 

  3. Ambainis, A.: Quantum walk algorithm for element distinctness. SIAM J. Comput. 37(1), 210 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  4. Gamble, J.K., Friesen, M., Zhou, D., Joynt, R., Coppersmith, S.: Two-particle quantum walks applied to the graph isomorphism problem. Phys. Rev. A 81(5), 052313 (2010)

    Article  ADS  Google Scholar 

  5. Childs, A.M.: Universal computation by quantum walk. Phys. Rev. Lett. 102(18), 180501 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  6. Lovett, N.B., Cooper, S., Everitt, M., Trevers, M., Kendon, V.: Universal quantum computation using the discrete-time quantum walk. Phys. Rev. A 81(4), 042330 (2010)

    Article  ADS  MathSciNet  Google Scholar 

  7. Štefaňák, M., Skoupỳ, S.: Perfect state transfer by means of discrete-time quantum walk on complete bipartite graphs. Quantum Inf. Process. 16(3), 72 (2017)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  8. Innocenti, L., Majury, H., Giordani, T., Spagnolo, N., Sciarrino, F., Paternostro, M., Ferraro, A.: Quantum state engineering using one-dimensional discrete-time quantum walks. Phys. Rev. A 96(6), 062326 (2017)

    Article  ADS  Google Scholar 

  9. Rohde, P.P., Fitzsimons, J.F., Gilchrist, A.: Quantum walks with encrypted data. Phys. Rev. Lett. 109(15), 150501 (2012)

    Article  ADS  Google Scholar 

  10. Wang, Y., Shang, Y., Xue, P.: Generalized teleportation by quantum walks. Quantum Inf. Process. 16(9), 221 (2017)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  11. Li, H.-J., Chen, X.-B., Wang, Y.-L., Hou, Y.-Y., Li, J.: A new kind of flexible quantum teleportation of an arbitrary multi-qubit state by multi-walker quantum walks. Quantum. Inf. Process. 18(9), 266 (2019)

    Article  ADS  Google Scholar 

  12. Vlachou, C., Krawec, W., Mateus, P., Paunković, N., Souto, A.: Quantum key distribution with quantum walks. Quantum Inf. Process. 17(11), 288 (2018)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  13. Yang, Y., Yang, J., Zhou, Y., Shi, W., Chen, X., Li, J., Zuo, H.: Quantum network communication: a discrete-time quantum-walk approach. Sci. China Inf. Sci. 61(4), 042501 (2018)

    Article  MathSciNet  Google Scholar 

  14. Chen, X.B., Wang, Y.L., Xu, G., Yang, Y.X.: Quantum network communication with a novel discrete-time quantum walk. IEEE Access 7, 13634 (2019)

    Article  Google Scholar 

  15. Farhi, E., Gutmann, S.: Quantum computation and decision trees. Phys. Rev. A 58(2), 915 (1998)

    Article  ADS  MathSciNet  Google Scholar 

  16. Brun, T.A., Carteret, H.A., Ambainis, A.: Quantum walks driven by many coins. Phys. Rev. A 67(5), 052317 (2003)

    Article  ADS  MathSciNet  Google Scholar 

  17. Liu, C., Petulante, N.: One-dimensional quantum random walks with two entangled coins. Phys. Rev. A 79(3), 032312 (2009)

    Article  ADS  Google Scholar 

  18. Liu, C.: Asymptotic distributions of quantum walks on the line with two entangled coins. Quantum Inf. Process. 11(5), 1193 (2012)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  19. Konno, N., Łuczak, T., Segawa, E.: Limit measures of inhomogeneous discrete-time quantum walks in one dimension. Quantum Inf. Process. 12(1), 33 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  20. Zhang, R., Xue, P., Twamley, J.: One-dimensional quantum walks with single-point phase defects. Phys. Rev. A 89(4), 042317 (2014)

    Article  ADS  Google Scholar 

  21. Suzuki, A.: Asymptotic velocity of a position-dependent quantum walk. Quantum Inf. Process. 15(1), 103 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  22. Montero, M.: Invariance in quantum walks with time-dependent coin operators. Phys. Rev. A 90(6), 062312 (2014)

    Article  ADS  Google Scholar 

  23. Yalçınkaya, İ., Gedik, Z.: Qubit state transfer via discrete-time quantum walks. J. Phys. A Math. Theor. 48(22), 225302 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  24. Montero, M.: Quantum and random walks as universal generators of probability distributions. Phys. Rev. A 95(6), 062326 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  25. Ekert, A.K.: Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67(6), 661 (1991)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  26. Xu, G., Chen, X.B., Dou, Z., Yang, Y.X., Li, Z.: A novel protocol for multiparty quantum key management. Quantum Inf. Process. 14(8), 2959 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  27. Bennett, C.H., Brassard, G., Crépeau, C., Jozsa, R., Peres, A., Wootters, W.K.: Teleporting an unknown quantum state via dual classical and Einstein–Podolsky–Rosen channels. Phys. Rev. Lett. 70(13), 1895 (1993)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  28. Xu, G., Chen, X.B., Dou, Z., Li, J., Liu, X., Li, Z.P.: Novel criteria for deterministic remote state preparation via the entangled six-qubit state. Entropy 18(7), 267 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  29. Chen, X.B., Sun, Y.R., Xu, G., Jia, H.Y., Qu, Z., Yang, Y.X.: Controlled bidirectional remote preparation of three-qubit state. Quantum Inf. Process. 16(10), 244 (2017)

    Article  ADS  MATH  Google Scholar 

  30. Hillery, M., Bužek, V., Berthiaume, A.: Quantum secret sharing. Phys. Rev. A 59(3), 1829 (1999)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  31. Xu, G., Chen, X.B., Li, J., Wang, C., Yang, Y.X., Li, Z.: Network coding for quantum cooperative multicast. Quantum Inf. Process. 14(11), 4297 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  32. Li, J., Chen, X.B., Xu, G., Yang, Y.X., Li, Z.P.: Perfect quantum network coding independent of classical network solutions. IEEE Commun. Lett. 19(2), 115 (2015)

    Article  ADS  Google Scholar 

  33. Li, Z.Z., Xu, G., Chen, X.B., Sun, X.M., Yang, Y.X.: Multi-user quantum wireless network communication based on multi-qubit GHZ state. IEEE Commun. Lett. 20(12), 2470 (2016)

    Article  Google Scholar 

  34. Li, J., Chen, X.B., Sun, X.M., Li, Z.P., Yang, Y.X.: Quantum network coding for multi-unicast problem based on 2D and 3D cluster states. Sci. China Inf. Sci. 59(4), 042301 (2016)

    Article  Google Scholar 

  35. Li, Z.Z., Xu, G., Chen, X.B., Qu, Z.G., Niu, X.X., Yang, Y.X.: Efficient quantum state transmission via perfect quantum network coding. Sci. China Inf. Sci. 62(1), 12501 (2019)

    Article  Google Scholar 

  36. Xu, G., Xiao, K., Li, Z., Niu, X.X., Ryan, M.: Controlled secure direct communication protocol via the three-qubit partially entangled set of states. CMC-Comput. Mater. Continua 58(3), 809 (2019)

    Article  Google Scholar 

  37. Wei, Z.H., Chen, X.B., Niu, X.X., Yang, Y.X.: The quantum steganography protocol via quantum noisy channels. Int. J. Theor. Phys. 54(8), 2505 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  38. Di Franco, C., Mc Gettrick, M., Busch, T.: Mimicking the probability distribution of a two-dimensional Grover walk with a single-qubit coin. Phys. Rev. Lett. 106(8), 080502 (2011)

    Article  Google Scholar 

  39. Venegas-Andraca, S.E.: Quantum walks: a comprehensive review. Quantum Inf. Process. 11(5), 1015 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  40. Shamir, A.: How to share a secret. Commun. ACM 22(11), 612 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  41. Li, J., Li, N., Zhang, Y., Wen, S., Du, W., Chen, W., Ma, W.: A survey on quantum cryptography. Chin. J. Electron. 27(2), 223 (2018)

    Article  Google Scholar 

  42. Chen, X.B., Su, Y., Xu, G., Sun, Y., Yang, Y.X.: Quantum state secure transmission in network communications. Inf. Sci. 276, 363 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  43. Wang, J.T., Xu, G., Chen, X.B., Sun, X.M., Jia, H.Y.: Local distinguishability of Dicke states in quantum secret sharing. Phys. Lett. A 381(11), 998 (2017)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  44. Chen, X.B., Tang, X., Xu, G., Dou, Z., Chen, Y.L., Yang, Y.X.: Cryptanalysis of secret sharing with a single d-level quantum system. Quantum Inf. Process. 17(9), 225 (2018)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  45. Chen, X.-B., Sun, Y.-R., Xu, G., Yang, Y.-X.: Quantum homomorphic encryption scheme with flexible number of evaluator based on (k, n)-threshold quantum state sharing. Inf. Sci. 501(10), 172–181 (2019)

    Article  MathSciNet  Google Scholar 

  46. Lance, A.M., Symul, T., Bowen, W.P., Sanders, B.C., Lam, P.K.: Tripartite quantum state sharing. Phys. Rev. Lett. 92(17), 177903 (2004)

    Article  ADS  Google Scholar 

  47. Li, Y., Zhang, K., Peng, K.: Multiparty secret sharing of quantum information based on entanglement swapping. Phys. Lett. A 324(5–6), 420 (2004)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  48. Li, D.F., Wang, R.J., Zhang, F.L., Deng, F.H., Baagyere, E.: Quantum information splitting of arbitrary two-qubit state by using four-qubit cluster state and Bell-state. Quantum Inf. Process. 14(3), 1103 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  49. Zheng, S.B.: Splitting quantum information via W states. Phys. Rev. A 74(5), 054303 (2006)

    Article  ADS  Google Scholar 

  50. Chen, X., Jiang, M., Chen, X.P., Li, H.: Quantum state sharing of an arbitrary three-qubit state by using three sets of W-class states. Quantum Inf. Process. 12(7), 2405 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  51. Muralidharan, S., Panigrahi, P.K.: Quantum information splitting using multipartite cluster states. Phys. Rev. A 78(6), 062333 (2008)

    Article  ADS  Google Scholar 

  52. Nie, Y.Y., Li, Y.H., Liu, J.C., Sang, M.H.: Quantum information splitting of an arbitrary three-qubit state by using two four-qubit cluster states. Quantum Inf. Process. 10(3), 297 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  53. Tao, Y., Tian, D., Hu, M., Qin, M.: Quantum state sharing of an arbitrary qudit state by using nonmaximally generalized GHZ state. Chin. Phys. B 17(2), 624 (2008)

    Article  ADS  Google Scholar 

  54. Jiang, M.: An optimized quantum information splitting scheme with multiple controllers. Quantum Inf. Process. 15(12), 5073 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  55. Qin, H., Tso, R.: Threshold quantum state sharing based on entanglement swapping. Quantum Inf. Process. 17, 1 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  56. Qin, H., Tso, R., Dai, Y.: Multi-dimensional quantum state sharing based on quantum Fourier transform. Quantum Inf. Process. 17(3), 48 (2018)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  57. Shi, R., Huang, L., Yang, W., Zhong, H.: Asymmetric five-party quantum state sharing of an arbitrary m-qubit state. Eur. Phys. J. D 57(2), 287 (2010)

    Article  ADS  Google Scholar 

  58. Shi, R.H., Huang, L.S., Yang, W., Zhong, H.: Asymmetric multi-party quantum state sharing of an arbitrary m-qubit state. Quantum Inf. Process. 10(1), 53 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  59. Maitra, A., De, S.J., Paul, G., Pal, A.K.: Proposal for quantum rational secret sharing. Phys. Rev. A 92(2), 022305 (2015)

    Article  ADS  Google Scholar 

  60. Dou, Z., Xu, G., Chen, X.B., Liu, X., Yang, Y.X.: A secure rational quantum state sharing protocol. Sci. China Inf. Sci. 61(2), 022501 (2018)

    Article  MathSciNet  Google Scholar 

  61. Wang, X.W., Xia, L.X., Wang, Z.Y., Zhang, D.Y.: Hierarchical quantum-information splitting. Opt. Commun. 283(6), 1196 (2010)

    Article  ADS  Google Scholar 

  62. Xu, G., Wang, C., Yang, Y.X.: Hierarchical quantum information splitting of an arbitrary two-qubit state via the cluster state. Quantum. Inf. Process. 13(1), 43–57 (2014)

    Article  ADS  MATH  Google Scholar 

  63. Ambainis, A., Bach, E., Nayak, A., Vishwanath, A., Watrous, J.: One-dimensional quantum walks. In: Proceedings of the Thirty-Third Annual ACM Symposium on Theory of Computing. ACM. pp. 37–49 (2001)

  64. Aharonov, D., Ambainis, A., Kempe, J., Vazirani, U.: Quantum walks on graphs. In: Proceedings of the Thirty-Third Annual ACM Symposium on Theory of Computing. ACM. pp. 50–59 (2001)

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant Nos. U1636106, 61671087, 61170272, 61962009), Natural Science Foundation of Beijing Municipality (No. 4182006), Technological Special Project of Guizhou Province (Grant No. 20183001), and the Foundation of Guizhou Provincial Key Laboratory of Public Big Data (Grant Nos. 2018BDKFJJ016, 2018BDKFJJ018).

Author information

Authors and Affiliations

  1. School of Computer Science, Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Heng-Ji Li, Jian Li & Yan Zheng

  2. Information Security Center, State Key Laboratory Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Heng-Ji Li & Nan Xiang

  3. Center for Quantum Information Research, ZaoZhuang University, ZaoZhuang, 277160, Shandong, China

    Jian Li

  4. Faculty of Information Technology, Beijing University of Technology, Beijing, 100124, China

    Yu-Guang Yang

  5. Department of Physics, Kermanshah Branch, Islamic Azad University, Kermanshah, Iran

    Mosayeb Naseri

Authors
  1. Heng-Ji Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jian Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Nan Xiang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Yan Zheng
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Yu-Guang Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Mosayeb Naseri
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jian Li.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, HJ., Li, J., Xiang, N. et al. A new kind of universal and flexible quantum information splitting scheme with multi-coin quantum walks. Quantum Inf Process 18, 316 (2019). https://doi.org/10.1007/s11128-019-2422-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-019-2422-3

Keywords