Abstract
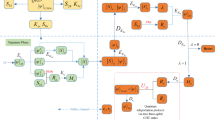
Quantum group signature is an important branch of quantum signature. Most of the existing quantum group signature schemes require that all the signatories must be present to generate a valid signature, and this property may limit their application in practice. In this paper, we will propose a quantum (t, n) threshold group signature scheme. In our scheme, n signatories compose a group, and any t out of these n signatories can generate a valid signature on behalf of the group. The t signatories use the quantum-controlled-not operations to expand the quantum message into t-particle entangled states, and then use the entanglement swapping to transmit the quantum message to the receiver. The receiver performs the single-particle measurements and unitary operations to recover the initial quantum message, and then verifies the signature with the help of the arbitrator. Compared to the existing quantum group signature schemes, our (t, n) threshold scheme will be more flexible in practice.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Rivest, R.L., Shamir, A., Aldleman, L.: A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 21, 120–126 (1978)
Shor, P.W.: Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 41, 303–332 (1996)
Gennaro, R., Rabin, T., Krawczyk, H.: RSA-based undeniable signatures. J. Cryptol. 13, 397–416 (2000)
Johnson, D., Menezes, A., Vanstone, S.: The elliptic curve digital signature algorithm (ECDSA). Int. J. Inf. Secur. 1, 36–63 (2001)
Buhrman, H., Cleve, R., Watrous, J., Wolf, R.D.: Quantum fingerprinting. Phys. Rev. Lett. 87, 167902 (2001)
Zeng, G.H., Keitel, C.H.: Arbitrated quantum-signature scheme. Phys. Rev. A 65, 042312 (2002)
Li, Q., Chan, W.H., Long, D.Y.: Arbitrated quantum signature scheme using Bell states. Phys. Rev. A 79, 054307 (2009)
Li, H.R., Luo, M.X., Peng, D.Y., Wang, X.J.: An arbitrated quantum signature scheme without entanglement. Commun. Theor. Phys. 68, 317–322 (2017)
Yang, Y.G., Lei, H., Liu, Z.C., Zhou, Y.H., Shi, W.M.: Arbitrated quantum signature scheme based on cluster states. Quantum Inf. Process. 15, 2487–2497 (2016)
Li, K., Shang, T., Liu, J.W.: Continuous-variable quantum homomorphic signature. Quantum Inf. Process. 16, 246 (2017)
Li, W., Shi, R.H., Guo, Y.: Blind quantum signature with blind quantum computation. Int. J. Theor. Phys. 56, 1108–1115 (2017)
Zhang, M.H., Li, H.F.: Fault-tolerant quantum blind signature protocols against collective noise. Quantum Inf. Process. 15, 4283–4301 (2016)
Shang, T., Lei, Q., Liu, J.W.: Quantum random oracle model for quantum digital signature. Phys. Rev. A 94, 042314 (2016)
Puthoor, I.V., Amiri, R., Wallden, P., Curty, M., Andersson, E.: Measurement-device-independent quantum digital signatures. Phys. Rev. A 94, 022328 (2016)
Amiri, R., Wallden, P., Kent, A., Andersson, E.: Secure quantum signatures using insecure quantum channels. Phys. Rev. A 93, 032325 (2016)
Yin, H.L., Fu, Y., Liu, H., et al.: Experimental quantum digital signature over 102 km. Phys. Rev. A 95, 032334 (2017)
Roberts, G.L., Lucamarini, M., Yuan, Z.L., et al.: Experimental measurement-device-independent quantum digital signatures. Nat. Commun. 8, 1098 (2017)
Yang, Y.G., Wen, Q.Y.: Quantum threshold group signature. Sci. China Phys. Mech. Astron. 51, 1505–1514 (2008)
Yang, Y.G., Wen, Q.Y.: Threshold proxy quantum signature scheme with threshold shared verification. Sci. China Phys. Mech. Astron. 51, 1079–1088 (2008)
Shamir, A.: How to share a secret. Commun. ACM 11, 612–613 (1979)
Shi, J.J., Shi, R.H., Guo, Y., Peng, X.Q., Lee, M.H., Park, D.S.: A (t, n)-threshold scheme of multi-party quantum group signature with irregular quantum Fourier transform. Int. J. Theor. Phys. 51, 1038–1049 (2012)
Bennett, C.H., Brassard, G.: Quantum cryptography: public-key distribution and coin tossing. In: IEEE International Conference on Computers, Systems, and Signal Processing, Bangalore, pp. 175–179 (1984)
Lo, H.K., Ma, X.F., Chen, K.: Decoy state quantum key distribution. Phys. Rev. Lett. 94, 230504 (2005)
Deng, F.G., Long, G.L.: Secure direct communication with a quantum one-time pad. Phys. Rev. A 69, 052319 (2004)
Hu, J.Y., Yu, B., Jing, M.Y., et al.: Experimental quantum secure direct communication with single photons. Light Sci. Appl. 5, e16144 (2016)
Boykin, P.O., Roychowdhury, V.: Optimal encryption of quantum bits. Phys. Rev. A 67, 042317 (2003)
Acknowledgements
This study is supported by Natural Science Foundation of China (Grant No. 61602247) and Natural Science Foundation of Jiangsu Province (Grant No. BK20160840).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Qin, H., Tang, W.K.S. & Tso, R. Quantum (t, n) threshold group signature based on Bell state. Quantum Inf Process 19, 71 (2020). https://doi.org/10.1007/s11128-019-2567-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-019-2567-0