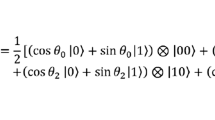Abstract
This comment analyzes and clarifies some questions proposed by Mastriani (Quantum Inf Process 16:27, 2017). These questions include the distinction between simulation verifications and quantum algorithms, the classical-to-quantum and quantum-to-classical interfaces, quantum measurement problem. Firstly, we propose that these questions are confusion, and even wrong. Then, we analyze the storage and computing performances of quantum Boolean image processing (QuBoIP), and conclude that QuBoIP has almost no significance for development of quantum image processing. Meanwhile, we describe how to verify the correctness of quantum algorithms using Matlab, and consider that the simulation verification of quantum algorithms is feasible on classic computers. Although quantum measurement is the open issue of quantum image processing, quantum image processing deserves further research and are significant. In conclusion, we believe that this comment is helpful for the developing of quantum image processing by clarifying these confusing questions proposed by Mario Mastriani.



Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Shor, P.W.: Algorithms for quantum computation: discrete logarithms and factoring. In: Proceedings of 35th Annual Symposium on Foundations of Computer Science, pp. 124–134. IEEE (1994)
Deutsch, D.: Quantum theory, the Church-Turing principle and the universal quantum computer. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 400, 97–117 (1985)
Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2000)
Beach, G., Lomont, C., Cohen, C.: Quantum image processing (QuIP). In: Proceedings of IEEE 32nd Applied Imagery Pattern Recognition Workshop, pp. 39–44 (2003)
Venegas-Andraca, S.E., Bose, S.: Quantum computation and image processing: new trends in artificial intelligence. In: Proceedings of the International Congress on Artificial Intelligence, pp. 1563–1564 (2003)
Venegas-Andraca, S.E., Bose, S.: Storing, processing, and retrieving an image using quantum mechanics. In: Proceedings of the SPIE Conference on Quantum Information and Computation, pp. 137–147 (2003)
Le, P.Q., Dong, F., Hirota, K.: A flexible representation of quantum images for polynomial preparation, image compression, and processing operations. Quantum Inf. Process. 10, 63–84 (2011)
Sun, B., Iliyasu, A., Yan, F., et al.: An rgb multi-channel representationfor images on quantum computers. J. Adv. Comput. Intell. Intell. Inform. 17(3), 404–417 (2013)
Li, H.S., Zhu, Q., Song, L., et al.: Image storage, retrieval, compression and segmentation in a quantum system. Quantum Inf. Process. 12(6), 2269–2290 (2013)
Li, H.S., Zhu, Q., Zhou, R.G., et al.: Multidimensional color image storage, retrieval, and compression based on quantum amplitudes and phases. Inf. Sci. 273, 212–232 (2014)
Li, H.S., Zhu, Q., Zhou, R.G., et al.: Multi-dimensional color image storage and retrieval for a normal arbitrary quantum superposition state. Quantum Inf. Process. 13(4), 991–1011 (2014)
Li, H.S., Fan, P., Xia, H.Y., et al.: Quantum implementation circuits of quantum signal representation and type conversion. IEEE Trans. Circuits Syst. I Regul. Pap. 99, 1–14 (2018)
Zhou, R.G., Wu, Q., Zhang, M.Q., et al.: Quantum image encryption and decryption algorithms based on quantum image geometric transformations. Int. J. Theor. Phys. 52(6), 1802–1817 (2013)
Zhang, Y., Lu, K., Gao, Y., et al.: NEQR: a novel enhanced quantum representation of digital images. Quantum Inf. Process. 12(8), 2283–2860 (2013)
Yuan, S., Mao, X., Xue, Y., et al.: SQR: a simple quantum representation of infrared images. Quantum Inf. Process. 13(6), 1353–1379 (2014)
Yan, F.F., Iliyasu, A.M., Venegas-Andraca, S.E.: survey of quantum image representations. Quantum Inf. Process. 15, 1–35 (2016)
Yan, F.F., Iliyasu, A.M., Jiang, Z.: Quantum computation-based image representation, processing operations and their applications. Entropy 16, 5290–5338 (2014)
Jiang, N., Wang, L.: Quantum image scaling using nearest neighbor interpolation. Quantum Inf. Process. 14(5), 1559–1571 (2015)
Abdolmaleky, M., Naseri, M., Batle, J., et al.: Red–Green–Blue multi-channel quantum representation of digital images. Optik 128, 121–132 (2017)
Yang, Y.G., Xia, J., Jia, X., et al.: Novel image encryption/decryption based on quantum Fourier transform and double phase encoding. Quantum Inf. Process. 12(11), 3477–3493 (2013)
Sang, J., Wang, S., Li, Q.: A novel quantum representation of color digital images. Quantum Inf. Process. 16(2), 1–14 (2017)
Li, H.S., Chen, X., Xia, H., et al.: A quantum image representation based on bitplanes. IEEE Access 6, 62396–62404 (2018)
Li, H.S., Fan, P., Xia, H.Y., et al.: The quantum Fourier transform based on quantum vision representation. Quantum Inf. Process. 17(12), 333 (2018)
Li, H.S., Fan, P., Xia, H.Y., et al.: The multi-level and multi-dimensional quantum wavelet packet transforms. Sci. Rep. 8(1), 13884 (2018)
Zhou, R.G., Hu, W., Fan, P., et al.: Quantum realization of the bilinear interpolation method for NEQR. Sci. Rep. 7(1), 2511 (2017)
Pang, C.Y., Zhou, R.G., Hu, B.Q., et al.: Signal and image compression using quantum discrete cosine transform. Inf. Sci. 473, 121–141 (2019)
Zhou, R.G., Yang, P.L., Liu, X.A., et al.: Quantum color image watermarking based on fast bit-plane scramble and dual embedded. Int. J. Quantum Inf. 16(07), 1850060 (2018)
Mastriani, M.: Quantum image processing? Quantum Inf. Process. 16, 27 (2017)
Mastriani, M.: Quantum Boolean image denoising. Quantum Inf. Process. 14, 1647–1673 (2014)
Hung, W.N., Song, X., Yang, G., et al.: Optimal synthesis of multiple output Boolean functions using a set of quantum gates by symbolic reachability analysis. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 25, 1652–1663 (2006)
Grover, L.: A fast quantum mechanical algorithm for database search. In: Proceedings of the 28th Annual ACM Symposium on the Theory of Computing, pp. 212–219 (1996)
Hu, B., Huang, X., Zhou, R., et al.: A theoretical framework for quantum image representation and data loading scheme. Sci. China Inf. Sci. 57, 032108 (2014)
Lin, C.C., Chakrabarti, A., Jha, N.K.: FTQLS: fault-tolerant quantum logic synthesis. IEEE Trans. Very Large Scale Integr. Syst. 22(6), 1350–1363 (2014)
Fan, P., Zhou, R.G., Jing, N., Li, H.S.: Geometric transformations of multidimensional color images based on NASS. Inf. Sci. 340, 191–208 (2016)
DiVincenzo, D.P.: Two-bit gates are universal for quantum computation. Phys. Rev. A 51, 1015–1022 (1995)
Yao, X., Wang, H., Liao, Z., et al.: Quantum image processing and its application to edge detection: theory and experiment. Phys. Rev. X 7, 031041 (2017)
Jiang, N., Dang, Y., Wang, J.: Quantum image matching. Quantum Inf. Process. 15, 3542–3572 (2016)
Acknowledgements
This work is supported by the National Natural Science Foundation of China under Grant Nos. 61462026, 61762012, and 61763014, the Science and Technology Project of Guangxi under Grant No. 2018JJA170083, the National Key R&D Plan under Grant Nos. 2018YFC1200200 and 2018YFC1200205, the Fund for Distinguished Young Scholars of Jiangxi Province under Grant No. 2018ACB2101, Natural Science Foundation of Jiangxi Province of China under Grant No. 20192BAB207014, Science and technology research project of Jiangxi Provincial Education Department under Grant No. GJJ190297. We thank the anonymous reviewers for their helpful feedback.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This comment refers to the article available online at https://doi.org/10.1007/s11128-016-1457-y.
Rights and permissions
About this article
Cite this article
Li, HS., Fan, P., Xia, Hy. et al. A comment on “Quantum image processing?”. Quantum Inf Process 19, 155 (2020). https://doi.org/10.1007/s11128-020-02654-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-020-02654-0