Fault-tolerant quantum error correction code preparation in UBQC

Abstract

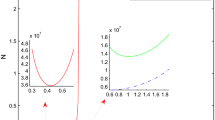
The universal blind quantum computation (UBQC) is a scheme to allow a client to delegate a computation to a remote server while concealing the input, output and algorithm. However, the qubit errors are inevitable in the practical application. In this paper, a fault-tolerant quantum error correction code preparation protocol with weak coherent pulses is proposed for fault-tolerant UBQC. Furthermore, the $\epsilon$-correctness and $\epsilon$-blindness of the protocol are fully proven. The simulation results show that the required number of pulses in our protocol is much less than that of the remote blind qubit state preparation protocol with two decoy states in case of the same probability of successful preparation, and is closer to asymptotic case.

Appendix

1.1 A. Quantum gates

In the quantum computation, a basic qubit unit is often stored on the polarization of a single photon or the spin of a single electron. A qubit has superposition property, which can be described by two-dimension Hilbert space. In quantum computation, an algorithm is described by the quantum circuit which consists of a sequence of quantum gates. In the circuit, each line (wire) represent a qubit, inputs are on the left and outputs on the right, with time flowing left to right. In two-qubit gates, the wire with a black dot represents a control bit and the other represents a target bit. The frequently used quantum gates have the Pauli gates, Hadamard gate H, controlled-NOT (CNOT) gate. The diagrammatic notations and the matrices forms of them are shown in Fig. 5.

Fig. 5

Diagram and matrix of quantum gates a Pauli-X gate, b Pauli-Y gate, c Pauli-Z gate, d Hadamard gate, e controlled-NOT (CNOT) gate

Two or more qubits can be entangled, which means that we are unable to know any of the qubits individually but we can learn the state of the whole system. For instance, a typical entanglement state called Bell states can be represented as$\left\{ {\frac{{\left| {00} \right\rangle \pm \left| {11} \right\rangle }}{{\sqrt{2} }},\frac{{\left| {01} \right\rangle \pm \left| {10} \right\rangle }}{{\sqrt{2} }}} \right\}$. In the practical system, the quantum state cannot be kept for a long time because of the environment and the imperfect devices, which is usually called the decoherence. However, the entangled qubits can be used to overcome the influence of the decoherence in the quantum computation. Hence, the entangled multi-qubits are used as quantum resources, such as cluster state and brickwork state  [8, 27]. In the paper, since we need cluster state to implement quantum gate in preparation process, the CNOT gate and Hadamard gates on the cluster state are given in Fig. 6.

Fig. 6

Realization of elementary quantum gates on the cluster state. a Hadamard gate, b general rotation gate, c CNOT gate between neighbouring logical qubits, d CNOT gate between two qubits separated by an even number of logical qubits, e CNOT gate between two qubits separated by an odd number of logical qubits

In Fig. 6, the pattern of (a) is used to realize the Hadamard gate. Each circle represents a qubit, and the lines represent entangling operators. The controlled-Z (CZ) gates are used to act on neighbouring qubits to prepare the entangled state. Each qubit is measured in a carefully chosen basis. The colour in each circle represents the measurement basis for the qubit. Circles in green denote cluster qubits measured in the eigenbasis of Pauli gate X, in red denoted as gate Y. The eigenbasis of quantum gate is called the measurement basis $M(\delta )$, $\delta$ is measurement angle. The eigenbasis of gate X corresponds to the angle $\delta =0$, and gate Y corresponds to $\delta =\pi /2$. The eigenbasis of gate Z is $\{|0\rangle ,|1\rangle \}$, and called the computational basis. The pattern of (b) is a general one-qubit rotation via one-qubit measurement on a cluster state. The angle $\pm \xi ,\pm \eta ,\pm \zeta$ specifying the measurement bases of the qubits are again dependent on the measurement results of other qubits. The pattern of (c) is CNOT gate between neighbouring logical qubits, and the patterns of (d) and (e) are CNOT gate between distant logical qubits, which can be adapted to any separation by repeating the section enclosed by the dashed line. In the quantum computation with cluster state, the redundant qubits are removed from the state by measuring in the computational basis, the other qubits are measured in the $M(\theta )$ basis to realize arbitrary quantum gate on a 2-D cluster state.

1.2 B. Quantum error correction code

In quantum computation, the errors are inevitable because of the de-coherence effect of quantum state. In order to correct qubit error, we need to establish a error model for quantum computation. In  [29], we conclude that the evolution of the qubit can be expressed as a linear combination of four possibilities: (1) no error occurs, (2) the bit flip $\left| 0\right\rangle \leftrightarrow \left| 1\right\rangle$, (3) the relation phase of $\left| 0\right\rangle$ and $\left| 1\right\rangle$, (4) both a bit flip and a phase flip occur. Then, the error superoperator $\mathcal{E}$ is diagonal in Pauli basis. The error model can be taken the form

$$\begin{aligned} \mathcal{E}\left( {\left| \psi \right\rangle \left\langle \psi \right| } \right) = \sum \limits _{{E_i} \in E} {p\left( {{E_i}} \right) } {E_i}\left| \psi \right\rangle \left\langle \psi \right| E_i^\dag , \end{aligned}$$

(6)

where all error $E_i$ are Pauli operators ${E_i} = \otimes _{j = 1}^nX_j^aZ_j^b,\;a,b \in \{ 0,1\}$, and $p\left( E_{i}\right)$ is the probability for the error $E_{i}$ to occur. In Eq. (6), we have the normalization condition $E_i^\dag E_i=\mathbf{I },\forall E_i$, and the trace-preserving constraint $\sum \limits _{{E_i} \in E} {p\left( {{E_i}} \right) }=1$. For correcting qubit errors, we need to diagnose which of these four possibilities actually occurred, then correct the error by applying the Pauli basis.

In the procedure for determining error syndrome, we must make sure that quantum state cannot be destroyed for subsequent quantum computation, and its information is private. Therefore, we need to use a suitable quantum code to handle these qubits, which may occur errors. A popular quantum code is the [[n, k, d]] stabilizer code  [29, 31, 32], which can encode k qubits into n. The parameter d is the distance of the code. A code with distance d can correct $\lfloor d/2\rfloor$ simultaneous errors from the error set E. The code space is the eigenspace of the generators of the code stabilizer S, which is a set of $(n-k)$ independent commuting operators g. Each codeword $\left| \psi _m\right\rangle$ obeys the eigenvalue equations $\left| \psi _m\right\rangle =g\left| \psi _m\right\rangle , \forall m=0,\ldots ,2^{k}-1$. The stabilizer code can be also described by the generator matrix G, which has 2n columns and $n-k$ rows. The generator matrix is denoted as $G=(X_{G}|Z_{G})$. Each row in G encodes a generator g of the stabilizer. The column index of $X_{G}$ and $Z_{G}$ labels the qubits. The positions of the 1’s in $X_{G}$ indicate the qubits that are acted on by X in the listed generators, and the 1’s in $Z_{G}$ indicated the qubits acted on by Z. If a 1 appears in same position in both $X_{G}$ and $Z_{G}$, then the product $Y=ZX$ acts on that qubit.

In the quantum error correction, the diagnosis of error is often named as the error syndrome measurement, which is increasingly difficult as the number of logical qubits increases in an encoded block. Hence, we use a common stabilizer code with fewer qubits, i.e. the 7-qubit Steane code [[7,1,3]], which can encode one qubit in seven, and corrects one-qubit error. The encoded logical qubit basis is denoted as $\{|0\rangle _{L},|1\rangle _{L}\}$.

$$\begin{aligned} {\left| 0 \right\rangle _L}&= \frac{1}{{2\sqrt{2} }}\left( {\left| {0000000} \right\rangle + \left| {0001111} \right\rangle + \left| {0110011} \right\rangle + \left| {0111100} \right\rangle } \right. \nonumber \\&\quad + \left. {\left| {1010101} \right\rangle + \left| {1011010} \right\rangle + \left| {1100110} \right\rangle + \left| {1101001} \right\rangle } \right) \nonumber \\ {\left| 1 \right\rangle _L}&= \frac{1}{{2\sqrt{2} }}\left( {\left| {1111111} \right\rangle + \left| {1110000} \right\rangle + \left| {1001100} \right\rangle + \left| {1000011} \right\rangle } \right. \nonumber \\&\quad + \left. {\left| {0101010} \right\rangle + \left| {0100101} \right\rangle + \left| {0011001} \right\rangle + \left| {0010110} \right\rangle } \right) \end{aligned}$$

(7)

In fact, the code is also a special case of the CSS code, which is an extension of the classical Hamming code in quantum error correction. The generator matrix of the [[7,1,3]] is shown as follows  [31]:

$$\begin{aligned} {G_{[[7,1,3]]}} = {({X_G}|{Z_G})_{[[7,1,3]]}} = \left( {\begin{array}{*{20}{c}} 0&{}0&{}0&{}1&{}1&{}1&{}1\\ 0&{}1&{}1&{}0&{}0&{}1&{}1\\ 1&{}0&{}1&{}0&{}1&{}0&{}1\\ 0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0 \end{array}\;\;\;\left| {\;\;\begin{array}{*{20}{c}} 0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}1&{}1&{}1&{}1\\ 0&{}1&{}1&{}0&{}0&{}1&{}1\\ 1&{}0&{}1&{}0&{}1&{}0&{}1 \end{array}} \right. } \right) . \end{aligned}$$

(8)

The encoding circuit of QECC can be designed according to the generator matrix. In Fig. 7a, the circuit is used to encode an unknown logical qubit  [29]. The CNOT gates of the circuit are based on $X_{G}$. In Fig. 7b, two ancilla states are prepared to perform error syndrome measurements of bit flip and phase flip. The measurement results of ancilla qubits are multiplied by the row vectors of $G_{[[7,1,3]]}$ to obtain the parity bits, which can diagnose the error syndrome. Then, we can use Pauli operator to correct the qubit errors in the encoded data block.

Fig. 7

The encoding and correction circuits of the [[7,1,3]] code  [29]. a An unknown logical qubit and 6 ancilla qubits can be used to encode into [[7,1,3]] code. b Two 7-qubit Steane states are used to correct error qubits for an 7-qubit data block. Each CNOT gate in the diagram represents 7 CNOT gates performed in parallel