Detection of genuine tripartite entanglement in quantum network scenario

Abstract

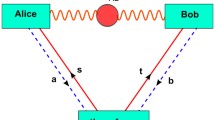
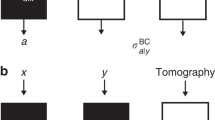
Experimental demonstration of entanglement needs to have a precise control of experimentalist over the system on which the measurements are performed as prescribed by an appropriate entanglement witness. To avoid such trust problem, recently, device-independent entanglement witnesses (DIEWs) for genuine tripartite entanglement have been proposed where witnesses are capable of testing genuine entanglement without precise description of Hilbert space dimension and measured operators i.e. apparatus are treated as black boxes. Here, we design a protocol for enhancing the possibility of identifying genuine tripartite entanglement in a device independent manner. We consider three mixed tripartite quantum states none of whose genuine entanglement can be detected by applying certain DIEWs, but their genuine tripartite entanglement can be detected by applying the same when distributed in some suitable entanglement swapping network.

Appendix A: Condition for violation of DIEWs

We are now going to enlist the DIEWs which are used as tools for DIED in main text.

Mermin DIEW [18]:

$$\begin{aligned} M = |\langle A_1B_0C_0\rangle + \langle A_0B_1C_0\rangle + \langle A_0B_0C_1\rangle - \langle A_1B_1C_1 \rangle | \le 2\sqrt{2}. \end{aligned}$$

(A1)

Uffink DIEW [20] :

$$\begin{aligned}&\langle A_1B_0C_0 + A_0B_1C_0 + A_0B_0C_1 - A_1B_1C_1 \rangle ^2 +\nonumber \\&\langle A_1B_1C_0 + A_0B_1C_1 + A_1B_0C_1 - A_0B_0C_0 \rangle ^2 \le 8. \end{aligned}$$

(A2)

Bancal et al. DIEW [22] : already discussed in Eq. (10).

Liang et al. DIEW [24] :

$$\begin{aligned}&\frac{1}{4}(\langle A_0B_0C_0\rangle + \langle A_0B_1C_0\rangle + \langle A_0B_0C_1\rangle + \langle A_0B_1C_1\rangle +\nonumber \\&\quad \langle A_1B_0C_0\rangle + \langle A_1B_1C_0\rangle +\langle A_1B_0C_1\rangle - 3 \langle A_1B_1C_1\rangle ) \le \sqrt{2}. \end{aligned}$$

(A3)

Now, we present the detailed proofs of the results stated in the main text. To obtain the condition of violation of each of the DIEWs (Eqs. A1, A2, 10, A3) in terms of state parameters for each of the initial states $\rho _i (i = 1, 2, 3)$ and final state $\rho _4$, we apply the same method as used in [55]. First, we find the condition of violation (in terms of state parameters) of the DIEW given in Eq. (A1) for the initial state $\rho _1$. We consider the following measurements: $A_0 = {\vec {x}}.\vec {\sigma _1}$ or $A_1 = \vec {\acute{x}}.\vec {\sigma _1}$ on $1^{st}$ qubit, $B_0 = \vec {y}.\vec {\sigma _2}$ or $B_1 = \vec {\acute{y}}.\vec {\sigma _2}$ on $2^{nd}$ qubit, and $C_0 = \vec {z}.\vec {\sigma _3}$ or $C_1 = \vec {\acute{z}}.\vec {\sigma _3}$ on $3^{rd}$ qubit, where $\vec {x},\vec {\acute{x}},\vec {y},\vec {\acute{y}}$ and $\vec {z},\vec {\acute{z}}$ are unit vectors and $\sigma _i$ are the spin projection operators that can be written in terms of the Pauli matrices. Representing the unit vectors in spherical coordinates, we have, $\vec {x} = (\sin \theta a_0 \cos \phi a_0, \sin \theta a_0 \sin \phi a_0, \cos \theta a_0), ~~\vec {y} = (\sin \alpha b_0 \cos \beta b_0, \sin \alpha b_0 \sin \beta b_0, \cos \alpha b_0)$ and $\vec {z} = (\sin \zeta c_0 \cos \eta c_0, \sin \zeta c_0 \sin \eta c_0, \cos \zeta c_0)$ and similarly, we define, $\vec {\acute{x}},\vec {\acute{y}}$ and $\vec {\acute{z}}$ by replacing 0 in the indices by 1. Then, the value of the operator M (Eq. A1) with respect to the state $\rho _1$ (Eq. 6) gives:

$$\begin{aligned} M(\rho _1)= & {} -\cos \alpha b_1 (-1 + p + p \cos 2 \theta )(\cos \zeta c_0\cos \theta a_1+\cos \zeta c_1\cos \theta a_0)\nonumber \\&-\sin \alpha b_1(p \sin 2\theta )(\cos (\beta b_1+\eta c_1+\phi a_0)\sin \zeta c_1\sin \theta a_0\nonumber \\&+\cos (\beta b_1+\eta c_0 +\phi a_1)\sin \zeta c_0\sin \theta a_1)\nonumber \\&+\cos \alpha b_0 (-1 + p + p \cos 2 \theta )(\cos \zeta c_0\cos \theta a_0-\cos \zeta c_1\cos \theta a_1)+\nonumber \\&\quad \sin \alpha b_0(p \sin 2\theta )(\cos (\beta b_0+\eta c_0+\phi a_0)\sin \zeta c_0\sin \theta a_0\nonumber \\&-\cos (\beta b_0+\eta c_1+\phi a_1)\sin \zeta c_1\sin \theta a_1). \end{aligned}$$

(A4)

Hence, in order to get maximum value of $S(\rho _1)$, we have to perform maximization over 12 measurement angles. Now if we maximize the last equation with respect to $\alpha b_0$ and $\alpha b_1$, we have

$$\begin{aligned}&M(\rho _1) \le \sqrt{((X)(\cos \zeta c_0\cos \theta a_1+\cos \zeta c_1\cos \theta a_0))^2+(Y)^2(A_{110}\sin \zeta c_1\sin \theta a_0 + A_{101}\sin \zeta c_0\sin \theta a_1)^2}\nonumber \\&\quad + \sqrt{((X)(\cos \zeta c_0\cos \theta a_0-\cos \zeta c_1\cos \theta a_1))^2 +(Y)^2(A_{000}\sin \zeta c_0\sin \theta a_0-A_{011}\sin \zeta c_1\sin \theta a_1)^2} \end{aligned}$$

(A5)

Where $X = -1 + p + p \cos 2 \theta$, $Y = p \sin 2\theta$, and $A_{ijk} = \cos (\beta b_i+\eta c_j +\phi a_k) (i, j, k \in \{0,1\})$. The last inequality is obtained by using the inequality $x\cos \theta + y \sin \theta \le \sqrt{x^2 + y^2}$. It is clear from the symmetry of the measurement angles $\theta a_0$ , $\zeta c_0$ and $\theta a_1$ , $\zeta c_1$ that the right-hand side of Eq. (A5) gives maximum value when $\theta a_0 = \zeta c_0$ and $\theta a_1 = \zeta c_1$. Hence, Eq. (A5) takes the form:

$$\begin{aligned}&M(\rho _1) \le \sqrt{((X)(2\cos \theta a_0\cos \theta a_1))^2+(Y \sin \theta a_0\sin \theta a_1)^2(A_{110} + A_{101})^2} +\nonumber \\&\quad \sqrt{((X)(\cos ^2\theta a_0-\cos ^2\theta a_1))^2 +(Y)^2(A_{000}\sin ^2\theta a_0-A_{011}\sin ^2\theta a_1)^2} \end{aligned}$$

(A6)

Again, we maximize it with respect to $\theta a_1$. Critical point 0 or $\frac{\pi }{2}$ gives the maximum value depending on values of the state parameters. For the critical point 0, Eq. (A6) becomes

$$\begin{aligned} M(\rho _1) \le \sqrt{(2 X \cos \theta a_0)^2} + \sqrt{\sin ^4\theta a_0(X^2+Y^2)} \end{aligned}$$

(A7)

where we have chosen $A^2_{000} = 1$. Maximizing over $\theta a_{0}$, we get

$$\begin{aligned} M(\rho _1) \le \frac{2 X^2 + Y^2}{\sqrt{X^2+Y^2}} \end{aligned}$$

(A8)

the maximum being obtained for $\cos \theta a_0 = \frac{|X|}{\sqrt{X^2 + Y^2}}$. For the other critical point $\frac{\pi }{2}$, Eq. (A6) takes the form:

$$\begin{aligned}&M(\rho _1) \le \sqrt{(Y \sin \theta a_0)^2(A_{110} + A_{101})^2}\nonumber \\&\qquad + \sqrt{X^2\cos ^4\theta a_0 + Y^2(A_{000}\sin ^2\theta a_0-A_{011})^2}\nonumber \\&\quad \le \sqrt{4(Y \sin \theta a_0)^2} + \sqrt{X^2\cos ^4\theta a_0 + Y^2(\sin ^2\theta a_0+1)^2}\nonumber \\&\le 4 |Y| \end{aligned}$$

(A9)

The second inequality in Eq. (A9) is obtained from the first by setting $A_{110} = 1$, $A_{101} = 1$, $A_{000} = 1$ and $A_{011} = -1.$ The final inequality is achieved when $\theta a_0 = \frac{\pi }{2}$ . Two sets of measurement angles which realize the two values $\frac{2 X^2 + Y^2}{\sqrt{X^2+Y^2}}$ (Eq. A8) and 4|Y| (Eq. A9), are $\theta a_0 = \alpha b_0 = \zeta c_0 = \cos ^{-1}(\frac{|X|}{\sqrt{X^2 + Y^2}})$, $\theta a_1 = \alpha b_1 = \zeta c_1 = 0$, $\beta b_i= \eta c_i = \phi a_i = 0$ (i = 0, 1) and $\theta a_i = \alpha b_i = \zeta c_i = \frac{\pi }{2}$(i = 0, 1) , $\beta b_0 = \eta c_0 = \phi a_0 = 0$, $\beta b_1 = -\eta c_1 = -\phi a_1 = \frac{\pi }{2}$, respectively. Hence, from Eq. (A8) and Eq. (A9), we have

$$\begin{aligned} M(\rho _1) \le \max [\frac{2 X^2 + Y^2}{\sqrt{X^2+Y^2}} , 4 |Y|] . \end{aligned}$$

(A10)

Clearly, $\frac{2 X^2 + Y^2}{\sqrt{X^2+Y^2}}\le 2 < 2 \sqrt{2}$ for any value of $p \in [0,1]$ and $0 \le \theta \le \frac{\pi }{4}.$ So the initial state $\rho _1$ violates the DIEW based on Mermin expression (Eq. A1) if

$$\begin{aligned} 4 |Y| = 4 | p | \sin 2\theta > 2 \sqrt{2} . \end{aligned}$$

(A11)

The last inequality is considered as the condition of violation of the DIEW based on Mermin expression for the initial state $\rho _1$. We have applied the same method over other states $\rho _i$ (i = 2, 3, 4)to find the condition of violation of the DIEW based on Mermin expression. For other DIEWS (Eqs. A2, 10, A3), we have made analysis in similar manner so as to obtain the condition of violation for each of states $\rho _i$. All the conditions are summarized in Table 1. However, among the four DIEWs given by Mermin (Eq. A1), Uffink (Eq. A2), Bancal et al. (Eq. 10) and Liang et al. (Eq. A3), the one given by Bancal et al. turns out to be the most efficient for this purpose. The DIEW based on Bancal et al. polynomial (Eq. 10) can thus detect genuine tripartite entanglement in a device-independent way in $\rho _1$ for $p > \frac{2}{3\sin 2\theta }$ (see Table 1). As $\frac{2}{3\sin 2\theta }< \frac{1}{\sqrt{2}\sin 2\theta } < \frac{3\sqrt{2}}{5\sin 2\theta }$, so the DIEW based on Bancal et al. polynomial (Eq. 10) is the most efficient DIEW for the state $\rho _1$ to detect genuine tripartite entanglement among all the standard DIEWs considered in Eqs. (A1), (A2), (10), (A3). Similarly by comparing the range of violation of $p_1$ (for the state $\rho _2$) and p (for the state $\rho _3$, $\rho _4$), one can check that Bancal et al. Bell inequality is the best DIEW for the other states $\rho _i$ (i = 2, 3, 4) to detect genuine tripartite entanglement compared to other standard DIEWs.