Skip to main content

Advertisement

Springer Nature Link
Log in

Machine learning on quantifying quantum steerability

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

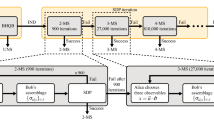
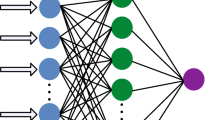
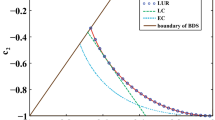
We apply the artificial neural network to quantify two-qubit steerability based on the steerable weight, which can be computed through semidefinite programming. Due to the fact that the optimal measurement strategy is unknown, it is still very difficult and time-consuming to efficiently obtain the steerability for an arbitrary quantum state. In this work, we show the method via machine learning technique which provides an effective way to quantify steerability. Furthermore, the generalization ability of the trained model is also demonstrated by applying to the Werner state and that in dephasing noise channel. Our findings provide an new way to obtain steerability efficiently and accurately, revealing effective application of the machine learning method on exploring quantum steering.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Schrodinger, E.: Discussion of probability relations between separated systems. Math. Proc. Camb. Philos. Soc. 31(4), 555 (1935). https://doi.org/10.1017/S0305004100013554

    Article  ADS  MATH  Google Scholar 

  2. Einstein, A., Podolsky, B., Rosen, N.: Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777 (1935). https://doi.org/10.1103/PhysRev.47.777

    Article  ADS  MATH  Google Scholar 

  3. Wiseman, H.M., Jones, S.J., Doherty, A.C.: Steering, entanglement, nonlocality, and the Einstein–Podolsky–Rosen paradox. Phys. Rev. Lett. 98, 140402 (2007). https://doi.org/10.1103/PhysRevLett.98.140402

    Article  ADS  MathSciNet  MATH  Google Scholar 

  4. Branciard, C., Cavalcanti, E.G., Walborn, S.P., Scarani, V., Wiseman, H.M.: One-sided device-independent quantum key distribution: security, feasibility, and the connection with steering. Phys. Rev. A 85, 010301 (2012). https://doi.org/10.1103/PhysRevA.85.010301

    Article  ADS  Google Scholar 

  5. Acín, A., Brunner, N., Gisin, N., Massar, S., Pironio, S., Scarani, V.: Device-independent security of quantum cryptography against collective attacks. Phys. Rev. Lett. 98, 230501 (2007). https://doi.org/10.1103/PhysRevLett.98.230501

    Article  ADS  Google Scholar 

  6. Passaro, E., Cavalcanti, D., Skrzypczyk, P., Acín, A.: Optimal randomness certification in the quantum steering and prepare-and-measure scenarios. New J. Phys. 17(11), 113010 (2015). https://doi.org/10.1088/1367-2630/17/11/113010

    Article  ADS  MATH  Google Scholar 

  7. Piani, M., Watrous, J.: Necessary and sufficient quantum information characterization of Einstein–Podolsky–Rosen steering. Phys. Rev. Lett. 114, 060404 (2015). https://doi.org/10.1103/PhysRevLett.114.060404

    Article  ADS  MathSciNet  Google Scholar 

  8. Cavalcanti, E.G., Jones, S.J., Wiseman, H.M., Reid, M.D.: Experimental criteria for steering and the Einstein–Podolsky–Rosen paradox. Phys. Rev. A 80, 032112 (2009). https://doi.org/10.1103/PhysRevA.80.032112

    Article  ADS  Google Scholar 

  9. Walborn, S.P., Salles, A., Gomes, R.M., Toscano, F., Souto Ribeiro, H.: Revealing hidden Einstein–Podolsky–Rosen nonlocality. Phys. Rev. Lett. 106, 130402 (2011). https://doi.org/10.1103/PhysRevLett.106.130402

    Article  ADS  Google Scholar 

  10. Schneeloch, J., Broadbent, C.J., Walborn, S.P., Cavalcanti, E.G., Howell, J.C.: Einstein–Podolsky–Rosen steering inequalities from entropic uncertainty relations. Phys. Rev. A 87, 062103 (2013). https://doi.org/10.1103/PhysRevA.87.062103

    Article  ADS  Google Scholar 

  11. Pramanik, T., Kaplan, M., Majumdar, A.S.: Fine-grained Einstein–Podolsky–Rosen—steering inequalities. Phys. Rev. A 90, 050305 (2014). https://doi.org/10.1103/PhysRevA.90.050305

    Article  ADS  Google Scholar 

  12. Kogias, I., Skrzypczyk, P., Cavalcanti, D., Acín, A., Adesso, G.: Hierarchy of steering criteria based on moments for all bipartite quantum systems. Phys. Rev. Lett. 115, 210401 (2015). https://doi.org/10.1103/PhysRevLett.115.210401

    Article  ADS  Google Scholar 

  13. Das, D., Sasmal, S., Roy, S.: Detecting Einstein–Podolsky–Rosen steering through entanglement detection. Phys. Rev. A 99, 052109 (2019). https://doi.org/10.1103/PhysRevA.99.052109

    Article  ADS  MathSciNet  Google Scholar 

  14. Chen, C., Ren, C., Ye, X.J., Chen, J.L.: Mapping criteria between nonlocality and steerability in qudit–qubit systems and between steerability and entanglement in qubit–qudit systems. Phys. Rev. A 98, 052114 (2018). https://doi.org/10.1103/PhysRevA.98.052114

    Article  ADS  Google Scholar 

  15. Yang, H., Ding, Z.Y., Wang, D., Yuan, H., Song, X.K., Yang, J., Zhang, C.J., Ye, L.: Experimental observation of Einstein–Podolsky–Rosen steering via entanglement detection. Phys. Rev. A 101, 042115 (2020). https://doi.org/10.1103/PhysRevA.101.042115

    Article  ADS  Google Scholar 

  16. Hsieh, C.Y., Liang, Y.C., Lee, R.K.: Quantum steerability: characterization, quantification, superactivation, and unbounded amplification. Phys. Rev. A 94, 062120 (2016). https://doi.org/10.1103/PhysRevA.94.062120

    Article  ADS  Google Scholar 

  17. Das, D., Datta, S., Jebaratnam, C., Majumdar, A.S.: Cost of Einstein–Podolsky–Rosen steering in the context of extremal boxes. Phys. Rev. A 97, 022110 (2018). https://doi.org/10.1103/PhysRevA.97.022110

    Article  ADS  Google Scholar 

  18. Kaur, E., Wang, X., Wilde, M.M.: Conditional mutual information and quantum steering. Phys. Rev. A 96, 022332 (2017). https://doi.org/10.1103/PhysRevA.96.022332

    Article  ADS  MathSciNet  Google Scholar 

  19. Ku, H.Y., Chen, S.L., Budroni, C., Miranowicz, A., Chen, Y.N., Nori, F.: Einstein–Podolsky–Rosen steering: its geometric quantification and witness. Phys. Rev. A 97, 022338 (2018). https://doi.org/10.1103/PhysRevA.97.022338

    Article  ADS  Google Scholar 

  20. Skrzypczyk, P., Navascués, M., Cavalcanti, D.: Quantifying Einstein–Podolsky–Rosen steering. Phys. Rev. Lett. 112, 180404 (2014). https://doi.org/10.1103/PhysRevLett.112.180404

    Article  ADS  Google Scholar 

  21. Vandenberghe, L., Boyd, S.: Semidefinite programming. SIAM Rev. 38(1), 49 (1996). https://doi.org/10.1137/1038003

    Article  MathSciNet  MATH  Google Scholar 

  22. Cavalcanti, D., Skrzypczyk, P.: Quantum steering: a review with focus on semidefinite programming. Rep. Prog. Phys. 80(2), 024001 (2016). https://doi.org/10.1088/1361-6633/80/2/024001

    Article  ADS  MathSciNet  Google Scholar 

  23. Bishop, C.: Pattern Recognition and Machine Learning. Springer, New York (2006)

    MATH  Google Scholar 

  24. Carleo, G., Cirac, I., Cranmer, K., Daudet, L., Schuld, M., Tishby, N., Vogt-Maranto, L., Zdeborová, L.: Machine learning and the physical sciences. Rev. Mod. Phys. 91, 045002 (2019). https://doi.org/10.1103/RevModPhys.91.045002

    Article  ADS  Google Scholar 

  25. Ch’ng, K., Carrasquilla, J., Melko, R.G., Khatami, E.: Machine learning phases of strongly correlated fermions. Phys. Rev. X 7, 031038 (2017). https://doi.org/10.1103/PhysRevX.7.031038

    Article  Google Scholar 

  26. Yoshioka, N., Akagi, Y., Katsura, H.: Learning disordered topological phases by statistical recovery of symmetry. Phys. Rev. B 97, 205110 (2018). https://doi.org/10.1103/PhysRevB.97.205110

    Article  ADS  Google Scholar 

  27. Torlai, G., Mazzola, G., Carrasquilla, J., Troyer, M.: Neural-network quantum state tomography. Nat. Phys 14, 447 (2018). https://doi.org/10.1038/s41567-018-0048-5

    Article  Google Scholar 

  28. Deng, D.L.: Machine learning detection of bell nonlocality in quantum many-body systems. Phys. Rev. Lett. 120, 240402 (2018). https://doi.org/10.1103/PhysRevLett.120.240402

    Article  ADS  MathSciNet  Google Scholar 

  29. Canabarro, A., Brito, S., Chaves, R.: Machine learning nonlocal correlations. Phys. Rev. Lett. 122, 200401 (2019). https://doi.org/10.1103/PhysRevLett.122.200401

    Article  ADS  Google Scholar 

  30. Ren, C., Chen, C.: Steerability detection of an arbitrary two-qubit state via machine learning. Phys. Rev. A 100, 022314 (2019). https://doi.org/10.1103/PhysRevA.100.022314

    Article  ADS  Google Scholar 

  31. Nielsen, M.A.: Neural Networks and Deep Learning. Determination Press, New York (2015)

    Google Scholar 

  32. Werner, R.F.: Quantum states with Einstein–Podolsky–Rosen correlations admitting a hidden-variable model. Phys. Rev. A 40, 4277 (1989). https://doi.org/10.1103/PhysRevA.40.4277

    Article  ADS  MATH  Google Scholar 

  33. Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2010)

    Book  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China under Grant Nos. 11805065 and 11504106, the Natural Science and Technology Foundation of Guizhou Province under Grant No. [2017]7343, the Key laboratory of low dimensional condensed matter physics of higher educational institution of Guizhou province (Grant No.[2016]002) and also by the Fundamental Research Funds for the Central Universities (Grant No. 2018072).

Author information

Authors and Affiliations

  1. Department of Mathematics and Physics, North China Electric Power University, Beijing, 102206, China

    Ye-Qi Zhang, Li-Juan Yang & Liang Chen

  2. School of Physics and Electronics, Guizhou Normal University, Guiyang, 550001, China

    Qi-Liang He

Authors
  1. Ye-Qi Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Li-Juan Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Qi-Liang He
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Liang Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Ye-Qi Zhang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, YQ., Yang, LJ., He, QL. et al. Machine learning on quantifying quantum steerability. Quantum Inf Process 19, 263 (2020). https://doi.org/10.1007/s11128-020-02769-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-020-02769-4

Keywords