Skip to main content

Advertisement

Springer Nature Link
Log in

Quantum phase transitions and scaling behaviors of extended 1D compass spin-chain model

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

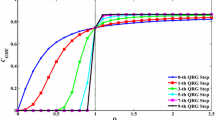
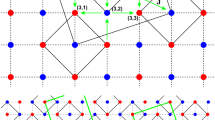
We use multipartite entanglement and trace distance to detect the quantum phase transitions of the extended one-dimensional compass spin-chain model by applying the density matrix renormalization group method which is represented by the matrix product state. It is shown that singular behaviors of the first-order derivative of the multipartite entanglement and trace distance occur at the critical point of the system. The scaling behaviors of trace distance and multipartite entanglement are also discussed, and we show that the universal finite-size scaling law is valid for the multipartite entanglement and trace distance around the critical point. Moreover, we explore the quantum coherence for this model and find that the first-order derivative of the quantum coherence also displays discontinuity and exhibits singular critical behaviors that are the same as the trace distance and multipartite entanglement.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Amico, L., Fazio, R., Osterloh, A., Vedral, V.: Entanglement in many-body systems. Rev. Mod. Phys. 80, 517–576 (2008). https://doi.org/10.1103/RevModPhys.80.517

    Article  ADS  MathSciNet  MATH  Google Scholar 

  2. Wu, L.A., Sarandy, M.S., Lidar, D.A.: Quantum phase transitions and bipartite entanglement. Phys. Rev. Lett. 93, 250404 (2004). https://doi.org/10.1103/PhysRevLett.93.250404

    Article  ADS  MathSciNet  Google Scholar 

  3. Sachdev, S.: Quantum Phase Transitions. Cambridge University Press, Cambridge (1999)

    MATH  Google Scholar 

  4. Gu, S.J., Lin, H.Q., Li, Y.Q.: Entanglement, quantum phase transition, and scaling in the \(XXZ\) chain. Phys. Rev. A 68, 042330 (2003). https://doi.org/10.1103/PhysRevA.68.042330

    Article  ADS  Google Scholar 

  5. Chen, J.J., Cui, J., Zhang, Y.R., Fan, H.: Coherence susceptibility as a probe of quantum phase transitions. Phys. Rev. A 94, 022112 (2016). https://doi.org/10.1103/PhysRevA.94.022112

    Article  ADS  Google Scholar 

  6. Gilchrist, A., Langford, N.K., Nielsen, M.A.: Distance measures to compare real and ideal quantum processes. Phys. Rev. A 71, 062310 (2005). https://doi.org/10.1103/PhysRevA.71.062310

    Article  ADS  Google Scholar 

  7. Gu, S.J.: Fidelity approach to quantum phase transitions. Int. J. Mod. Phys. B 24(23), 4371–4458 (2010)

    Article  ADS  MathSciNet  Google Scholar 

  8. Bennett, C.H., Bernstein, H.J., Popescu, S., Schumacher, B.: Concentrating partial entanglement by local operations. Phys. Rev. A 53, 2046–2052 (1996). https://doi.org/10.1103/PhysRevA.53.2046

    Article  ADS  Google Scholar 

  9. Wootters, W.K.: Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245–2248 (1998). https://doi.org/10.1103/PhysRevLett.80.2245

    Article  ADS  MATH  Google Scholar 

  10. Osborne, T.J., Verstraete, F.: General monogamy inequality for bipartite qubit entanglement. Phys. Rev. Lett. 96, 220503 (2006). https://doi.org/10.1103/PhysRevLett.96.220503

    Article  ADS  Google Scholar 

  11. Bai, Y.K., Xu, Y.F., Wang, Z.D.: General monogamy relation for the entanglement of formation in multiqubit systems. Phys. Rev. Lett. 113, 100503 (2014). https://doi.org/10.1103/PhysRevLett.113.100503

    Article  ADS  Google Scholar 

  12. Breuer, H.P., Laine, E.M., Piilo, J.: Measure for the degree of non-Markovian behavior of quantum processes in open systems. Phys. Rev. Lett. 103, 210401 (2009). https://doi.org/10.1103/PhysRevLett.103.210401

    Article  ADS  MathSciNet  Google Scholar 

  13. Smirne, A., Breuer, H.P., Piilo, J., Vacchini, B.: Initial correlations in open-systems dynamics: the Jaynes–Cummings model. Phys. Rev. A 82, 062114 (2010). https://doi.org/10.1103/PhysRevA.82.062114

    Article  ADS  Google Scholar 

  14. Luo, D.W., Xu, J.B.: Trace distance and scaling behavior of a coupled cavity lattice at finite temperature. Phys. Rev. A 87, 013801 (2013). https://doi.org/10.1103/PhysRevA.87.013801

    Article  ADS  Google Scholar 

  15. Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2000)

    MATH  Google Scholar 

  16. Engel, G.S., Calhoun, T.R., Read, E.L., Ahn, T.K., Mancal, T., Cheng, Y.C., Blankenship, R.E., Fleming, G.R.: Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 446(7137), 782–786 (2007). https://doi.org/10.1038/nature05678

    Article  ADS  Google Scholar 

  17. Collini, E., Wong, C.Y., Wilk, K.E., Curmi, P.M.G., Brumer, P., Scholes, G.D.: Coherently wired light-harvesting in photosynthetic marine algae at ambient temperature. Nature 463(7281), 644–647 (2010). https://doi.org/10.1038/nature08811

    Article  ADS  Google Scholar 

  18. Sachdev, S.: Quantum phase transitions. In: Handbook of Magnetism and Advanced Magnetic Mate rials. Wiley Online Library (2007). https://doi.org/10.1002/9780470022184.hmm108

  19. Radhakrishnan, C., Parthasarathy, M., Jambulingam, S., Byrnes, T.: Distribution of quantum coherence in multipartite systems. Phys. Rev. Lett. 116, 150504 (2016). https://doi.org/10.1103/PhysRevLett.116.150504

    Article  ADS  Google Scholar 

  20. Baumgratz, T., Cramer, M., Plenio, M.B.: Quantifying coherence. Phys. Rev. Lett. 113, 140401 (2014). https://doi.org/10.1103/PhysRevLett.113.140401

    Article  ADS  Google Scholar 

  21. White, S.R.: Density-matrix algorithms for quantum renormalization groups. Phys. Rev. B 48, 10345–10356 (1993). https://doi.org/10.1103/PhysRevB.48.10345

    Article  ADS  Google Scholar 

  22. White, S.R.: Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 69, 2863–2866 (1992). https://doi.org/10.1103/PhysRevLett.69.2863

    Article  ADS  Google Scholar 

  23. Wilson, K.G.: The renormalization group: critical phenomena and the Kondo problem. Rev. Mod. Phys. 47, 773–840 (1975). https://doi.org/10.1103/RevModPhys.47.773

    Article  ADS  MathSciNet  Google Scholar 

  24. Vidal, G.: Efficient simulation of one-dimensional quantum many-body systems. Phys. Rev. Lett. 93, 040502 (2004). https://doi.org/10.1103/PhysRevLett.93.040502

    Article  ADS  Google Scholar 

  25. Schollwöck, U.: The density-matrix renormalization group. Rev. Mod. Phys. 77, 259–315 (2005). https://doi.org/10.1103/RevModPhys.77.259

    Article  ADS  MathSciNet  MATH  Google Scholar 

  26. He, Y.C., Chen, Y.: Distinct spin liquids and their transitions in spin-1/2 \(xxz\) kagome antiferromagnets. Phys. Rev. Lett. 114, 037201 (2015). https://doi.org/10.1103/PhysRevLett.114.037201

    Article  ADS  Google Scholar 

  27. Schollwöck, U.: The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 326(1), 96–192 (2011). https://doi.org/10.1016/j.aop.2010.09.012

    Article  ADS  MathSciNet  MATH  Google Scholar 

  28. Jafari, R.: Quantum phase transition in the one-dimensional extended quantum compass model in a transverse field. Phys. Rev. B 84, 035112 (2011). https://doi.org/10.1103/PhysRevB.84.035112

    Article  ADS  Google Scholar 

  29. Jackeli, G., Khaliullin, G.: Mott insulators in the strong spin–orbit coupling limit: from Heisenberg to a quantum compass and Kitaev models. Phys. Rev. Lett. 102, 017205 (2009). https://doi.org/10.1103/PhysRevLett.102.017205

    Article  ADS  Google Scholar 

  30. Milman, P., Maineult, W., Guibal, S., Guidoni, L., Douçot, B., Ioffe, L., Coudreau, T.: Topologically decoherence-protected qubits with trapped ions. Phys. Rev. Lett. 99, 020503 (2007). https://doi.org/10.1103/PhysRevLett.99.020503

    Article  ADS  Google Scholar 

  31. Douçotot, B., Feigel’man, M.V., Ioffe, L.B., Ioselevich, A.S.: Protected qubits and Chern-Simons theories in Josephson junction arrays. Phys. Rev. B 71, 024505 (2005). https://doi.org/10.1103/PhysRevB.71.024505

    Article  ADS  Google Scholar 

  32. Horodecki, R., Horodecki, P., Horodecki, M., Horodecki, K.: Quantum entanglement. Rev. Mod. Phys. 81, 865–942 (2009). https://doi.org/10.1103/RevModPhys.81.865

    Article  ADS  MathSciNet  MATH  Google Scholar 

  33. Coffman, V., Kundu, J., Wootters, W.K.: Distributed entanglement. Phys. Rev. A 61, 052306 (2000). https://doi.org/10.1103/PhysRevA.61.052306

    Article  ADS  Google Scholar 

  34. Bai, Y.K., Yang, D., Wang, Z.D.: Multipartite quantum correlation and entanglement in four-qubit pure states. Phys. Rev. A 76, 022336 (2007). https://doi.org/10.1103/PhysRevA.76.022336

    Article  ADS  Google Scholar 

  35. Liu, G.H., Li, W., You, W.L., Tian, G.S., Su, G.: Matrix product state and quantum phase transitions in the one-dimensional extended quantum compass model. Phys. Rev. B 85, 184422 (2012). https://doi.org/10.1103/PhysRevB.85.184422

    Article  ADS  Google Scholar 

  36. Chitambar, E., Hsieh, M.H.: Relating the resource theories of entanglement and quantum coherence. Phys. Rev. Lett. 117, 020402 (2016). https://doi.org/10.1103/PhysRevLett.117.020402

    Article  ADS  Google Scholar 

  37. Streltsov, A., Singh, U., Dhar, H.S., Bera, M.N., Adesso, G.: Measuring quantum coherence with entanglement. Phys. Rev. Lett. 115, 020403 (2015). https://doi.org/10.1103/PhysRevLett.115.020403

    Article  ADS  MathSciNet  Google Scholar 

  38. Cui, J., Cao, J.P., Fan, H.: Quantum-information approach to the quantum phase transition in the Kitaev honeycomb model. Phys. Rev. A 82, 022319 (2010). https://doi.org/10.1103/PhysRevA.82.022319

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (NSFC) (Grant No. 11975198) and the Fundamental Research Funds for the Central Universities (Grant No. 2020FZA3005 and 2019FZA3005).

Author information

Authors and Affiliations

  1. Zhejiang Institute of Modern Physics and Department of Physics, Zhejiang University, Hangzhou, 310027, People’s Republic of China

    Qi Chen & Jing-Bo Xu

  2. Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials, GPETR Center for Quantum Precision Measurement, Frontier Research Institute for Physics and SPTE, South China Normal University, Guangzhou, 510006, People’s Republic of China

    Guo-Qing Zhang

Authors
  1. Qi Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Guo-Qing Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Jing-Bo Xu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jing-Bo Xu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, Q., Zhang, GQ. & Xu, JB. Quantum phase transitions and scaling behaviors of extended 1D compass spin-chain model. Quantum Inf Process 19, 275 (2020). https://doi.org/10.1007/s11128-020-02780-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-020-02780-9

Keywords