The effect on (2, N, 2) Bell tests with distributed measurement dependence

Abstract

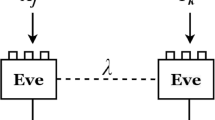
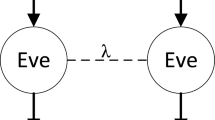
Bell tests, as primitive tools to detect nonlocality in bipartite systems, rely on an assumption, i.e., measurement independence. In practice, it is difficult to ensure measurement independence. It is necessary to investigate how Bell tests are affected by relaxing measurement independence. In the simplest (2, 2, 2) CHSH Bell test which consists of two parties, two measurements per party and two possible outcomes per measurement, the results between the maximal value of CHSH correlation function and distributed measurement dependence (DMD) are given, where DMD is a general measure of relaxing measurement independence. However, in a general Bell scenario of an arbitrary number of measurements per party, i.e., (2, N, 2), pertinent results are still missing. To solve it, we establish the relations between the maximal value of (2, N, 2) Pearle–Braunstein–Caves (PBC) chain correlation function that maintains the locality and the degree of DMD, denoted as DMD-induced PBC chain inequalities. Furthermore, we show the tightness of these derived inequalities via constructing local hidden variable models that fake the upper bounds. Compared with the simplest CHSH Bell test, our derived inequalities need less amount of measurement dependence to fake the quantum prediction with N increasing, which is beneficial to analyze the security of device-independent quantum information processing tasks such as randomness expansion.

Appendix

In order to prove the tightness of the derived results of Theorem 2, here, without loss of generality, we discuss the case of $N=3, \delta _A=\delta _B=1, \xi _A= \xi _B=1$, and other cases can be proved similarly.

For achieving the maximal value of PBC chain correlation function via local hidden variable model, then Eqs. (43), (44), (46) must hold “=.” Let absolute values of Eqs. (43), (44), (46) be themselves. Based on the product of definite outcomes of Alice and Bob (i.e, Table 5), then $p(\lambda |X_{0}Y_{0})-p(\lambda |X_{0}Y_{2})$, $p(\lambda |X_{1}Y_{1})-p(\lambda |X_{1}Y_{0})$, $p(\lambda |X_{2}Y_{2})-p(\lambda |X_{2}Y_{1})$, $p(\lambda |X_{1}Y_{0})-p(\lambda |X_{0}Y_{0})$ and $p(\lambda |X_{2}Y_{1})-p(\lambda |X_{1}Y_{1})$ need to satisfy the following relations:

$$\begin{aligned}&p(\lambda |X_{0}Y_{0})-p(\lambda |X_{0}Y_{2}) = \left\{ \begin{array}{ll} \le 0,\quad \ \ \lambda =1,3,4,5,6;\\ \ge 0,\quad \ \ \lambda =2. \end{array} \right. \end{aligned}$$

(60)

$$\begin{aligned}&p(\lambda |X_{1}Y_{1})-p(\lambda |X_{1}Y_{0}) = \left\{ \begin{array}{ll} \le 0,\quad \ \ \lambda =3, 4, 5;\\ \ge 0,\quad \ \ \lambda =1, 2, 6. \end{array} \right. \end{aligned}$$

(61)

$$\begin{aligned}&p(\lambda |X_{2}Y_{2})-p(\lambda |X_{2}Y_{1}) = \left\{ \begin{array}{ll} \le 0,\quad \ \ \lambda =3;\\ \ge 0,\quad \ \ \lambda =1, 2, 4, 5, 6. \end{array} \right. \end{aligned}$$

(62)

$$\begin{aligned}&p(\lambda |X_{1}Y_{0})-p(\lambda |X_{0}Y_{0}) = \left\{ \begin{array}{ll} \le 0,\quad \ \ \lambda =3, 4, 5, 6;\\ \ge 0,\quad \ \ \lambda =1, 2. \end{array} \right. \end{aligned}$$

(63)

$$\begin{aligned}&p(\lambda |X_{2}Y_{1})-p(\lambda |X_{1}Y_{1}) = \left\{ \begin{array}{ll} \le 0,\quad \ \ \lambda =3, 4;\\ \ge 0,\quad \ \ \lambda =1, 2, 5, 6. \end{array} \right. \end{aligned}$$

(64)

Table 5 Definite outcomes $A(X_{j}, \lambda )$ and $B(Y_{k}, \lambda )$ of Alice’s and Bob’s measurements for given hidden variable

In order to enforce to satisfy these conditions, we parameterize the conditional probabilities in Table 6.

Table 6 Parameterization of the conditional probability $p(\lambda |X_{j}, Y_{k})$ with constrains of (60)–(64)

When ${{\hat{M}}}_{A}=M_{A}$ and ${{\hat{M}}}_{B}=M_{B}$, the result under four-parameter description is reduced to the result under two-parameter description. If the upper bound of $\hbox {DMD}_2$-induced PBC chain inequality is achieved, then the values of $f_{s} (s\in \{1,\ldots , 36\})$ which consist of $\{p(\lambda |X_j, Y_k)\}$ are given in the following:

$$\begin{aligned}&f_1=\cdots =f_6=\frac{2-2M_{A}-3M_{B}}{12},\nonumber \\&f_7=f_{22}=f_{30}=f_{35}=\frac{3M_{A}+3M_{B}}{12},\nonumber \\&f_{11}=f_{12}=f_{17}=f_{26}=f_{27}=f_{32}=\frac{M_{B}}{12};\nonumber \\&f_{13}=f_{18}=f_{28}=f_{33}=\frac{3M_{A}-3M_{B}}{12};\nonumber \\&f_{8}=f_{9}=f_{10}=f_{14}=f_{15}=f_{16}=f_{19}=f_{20}=f_{21}\nonumber \\&\quad =f_{23}=f_{24}=f_{25}=f_{29}=f_{31}=f_{34}=f_{36}=0. \end{aligned}$$

(65)

In the case of distributed measurement dependence with four-parameter description, if $\delta _A=\delta _B=1, \xi _A=\xi _B=1$, let $M_{B}[X_j]$, $M_{A}[Y_k]$ satisfy the following constraints:

$$\begin{aligned} \begin{aligned}&M_{B}[X_1]={{\hat{M}}}_{B}, M_{A}[Y_0]={{\hat{M}}}_{A},\\&M_{B}[X_0]= M_{B}, M_{A}[Y_1]=M_{A},\\&M_{B}[X_2]= M_{B}, M_{A}[Y_2]=M_{A},\\ \end{aligned} \end{aligned}$$

(66)

where $j, k\in \{0, 1, 2\}$.

Based on the normalization of probability and the expression of $I^\mathrm{PBC}_{N=3}$, $I^\mathrm{PBC}_{N=3}$ is deduced as

$$\begin{aligned} I^\mathrm{PBC}_{N=3}=6-2(f_1+f_2+\cdots +f_6). \end{aligned}$$

(67)

$I^\mathrm{PBC}_{N=3}$ is required to achieve the upper bound (i.e., $4+{{\hat{M}}}_{A}+{{\hat{M}}}_{B}+ M_{A}+2M_{B}$ ); then, we have

$$\begin{aligned} 6-2(f_1+f_2+\cdots +f_6)=4+{{\hat{M}}}_{A}+{{\hat{M}}}_{B}+ M_{A}+2M_{B}. \end{aligned}$$

(68)

Based on the normalization of $\{p(\lambda |X_1,Y_0)\}$, we get

$$\begin{aligned} \begin{aligned}&f_7+f_{12}+f_{13}+f_{17}+f_{18}+f_{19}+f_{22}+f_{23}+f_{27}\\&\quad =1-(f_1+\cdots +f_6).\\ \end{aligned} \end{aligned}$$

(69)

Based on the constraints of Eq. (66) and the normalization of probability, we get

$$\begin{aligned} \begin{aligned}&f_8+f_{14}+f_{32}=f_{19}+f_{23}+f_{27}=\frac{{{\hat{M}}}_{B}}{2},\\&f_9+f_{15}+f_{30}+f_{33}=f_{18}+f_{22}=\frac{M_{A}}{2},\\&f_{10}+f_{16}+f_{26}+f_{31}+f_{34}=f_{17}=\frac{M_{B}}{2},\\&f_{11}=f_{12}+f_{21}+f_{25}+f_{29}+f_{36}=\frac{M_{B}}{2},\\&f_{7}+f_{13}=f_{20}+f_{24}+f_{28}+f_{35}=\frac{{{\hat{M}}}_{A}}{2},\\&f_7-f_{11}+f_{12}+f_{13}+f_{22}-f_{26}+f_{27}+f_{28}-f_{30}+f_{32}\\&\quad +f_{33}-f_{35}=M_{A}. \end{aligned} \end{aligned}$$

(70)

Combing with Eq. (65), by solving Eq. (70) we get the values of $f_{s} (s\in \{1,\cdots , 36\})$ in the following:

$$\begin{aligned} \begin{aligned}&f_1=\cdots =f_{6}=\frac{2-M_{A}-2M_{B}-{{\hat{M}}}_{A}-{{\hat{M}}}_{B}}{12}, f_7=\frac{{{\hat{M}}}_{A}+M_{B}}{4},\\&f_{11}=f_{12}=f_{17}=f_{26}=\frac{M_{B}}{2},\\&f_{13}=\frac{{{\hat{M}}}_{A}-M_{B}}{4}, f_{18}=f_{33}=\frac{M_{A}-M_{B}}{4},\\&f_{22}=f_{30}=\frac{M_{A}+M_{B}}{4},\\&f_{27}=f_{32}=\frac{{{\hat{M}}}_{B}}{2},\\&f_{28}=\frac{-M_{A}+M_{B}+2{{\hat{M}}}_{A}-2{{\hat{M}}}_{B}}{4},\\&f_{35}=\frac{M_{A}-M_{B}+2{{\hat{M}}}_{B}}{4},\\&f_{8}=f_{9}=f_{10}=f_{14}=f_{15}=f_{16}=f_{19}=f_{20}=f_{21}\\&\quad =f_{23}=f_{24}=f_{25}=f_{29}=f_{31}=f_{34}=f_{36}=0. \end{aligned} \end{aligned}$$

(71)

Relying on Eq. (71), each element of Table 4 is given. Hence, we complete the entities of Table 4 under conditions of $M_A\ge M_B$, ${{\hat{M}}}_A+{{\hat{M}}}_B+M_A+2M_B\le 2$, ${{\hat{M}}}_A \ge M_B$ and $-M_A+M_B+2{{\hat{M}}}_A -2 {{\hat{M}}}_B \ge 0$.

When ${{\hat{M}}}_A+{{\hat{M}}}_B+M_A+2M_B>2$, the calculation of the values of $p(\lambda |X_j,Y_k)$ is similar to the case of ${{\hat{M}}}_A+{{\hat{M}}}_B+M_A+2M_B\le 2$. The difference between the case of ${{\hat{M}}}_A+{{\hat{M}}}_B+M_A+2M_B>2$ and the case of ${{\hat{M}}}_A+{{\hat{M}}}_B+M_A+2M_B\le 2$ is the relation deduction of $\{f_s\}$ in case of ${{\hat{M}}}_A=M_A$ and ${{\hat{M}}}_B=M_B$ and calculation about $\{f_s\}$ in case of ${{\hat{M}}}_A, M_A, {{\hat{M}}}_B, M_B$. However, the deduction methods are similar to the case of ${{\hat{M}}}_A+{{\hat{M}}}_B+M_A+2M_B\le 2$ and omitted.