Skip to main content

Advertisement

Springer Nature Link
Log in

Enhancing nonlocal advantage of quantum coherence in correlated quantum channels

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

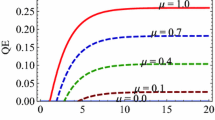
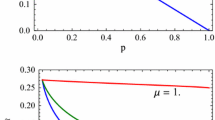
We explore decay behaviors of the nonlocal advantage of quantum coherence (NAQC) for two qubits traversing the phase flap, bit flip, bit-phase flip, and depolarizing channels. For the input Bell and Bell-diagonal states, we showed analytically that the NAQC of the output states can always be noticeably enhanced due to the correlations between consecutive uses of these quantum channels, and the degree of minimum correlation needed for achieving the NAQC increases with an increase in the decoherence factor. We also explored a colored dephasing channel which enables one to compare the cooperation mechanism of two different origins of memory effects in enhancing the NAQC.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Christandl, M., Datta, N., Ekert, A., Landahl, A.J.: Perfect state transfer in quantum spin networks. Phys. Rev. Lett. 92, 187902 (2004)

    ADS  Google Scholar 

  2. Bennett, C.H., Brassard, G., Crépeau, C., Jozsa, R., Peres, A., Wootters, W.K.: Teleporting an unknown quantum state via dual classical and Einstein–Podolsky–Rosen channels. Phys. Rev. Lett. 70, 1895 (1993)

    ADS  MathSciNet  MATH  Google Scholar 

  3. Bose, S.: Quantum communication through an unmodulated spin chain. Phys. Rev. Lett. 91, 207901 (2003)

    ADS  Google Scholar 

  4. Giovannetti, V., Lloyd, S., Maccone, L.: Quantum metrology. Phys. Rev. Lett. 96, 010401 (2006)

    ADS  MathSciNet  Google Scholar 

  5. Giovannetti, V., Lloyd, S., Maccone, L.: Advances in quantum metrology. Nat. Photonics 5, 222 (2011)

    ADS  Google Scholar 

  6. Horodecki, R., Horodecki, P., Horodecki, M., Horodecki, K.: Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009)

    ADS  MathSciNet  MATH  Google Scholar 

  7. Modi, K., Brodutch, A., Cable, H., Paterek, Z., Vedral, V.: The classical-quantum boundary for correlations: discord and related measures. Rev. Mod. Phys. 84, 1655 (2012)

    ADS  Google Scholar 

  8. Hu, M.L., Hu, X., Wang, J.C., Peng, Y., Zhang, Y.R., Fan, H.: Quantum coherence and geometric quantum discord. Phys. Rep. 762–764, 1–100 (2018)

    ADS  MathSciNet  MATH  Google Scholar 

  9. Baumgratz, T., Cramer, M., Plenio, M.B.: Quantifying coherence. Phys. Rev. Lett. 113, 140401 (2014)

    ADS  Google Scholar 

  10. Streltsov, A., Singh, U., Dhar, H.S., Bera, M.N., Adesso, G.: Measuring quantum coherence with entanglement. Phys. Rev. Lett. 115, 020403 (2015)

    ADS  MathSciNet  Google Scholar 

  11. Yuan, X., Zhou, H., Cao, Z., Ma, X.: Intrinsic randomness as a measure of quantum coherence. Phys. Rev. A 92, 022124 (2015)

    ADS  Google Scholar 

  12. Winter, A., Yang, D.: Operational resource theory of coherence. Phys. Rev. Lett. 116, 120404 (2016)

    ADS  Google Scholar 

  13. Napoli, C., Bromley, T.R., Cianciaruso, M., Piani, M., Johnston, N., Adesso, G.: Robustness of coherence: an operational and observable measure of quantum coherenc. Phys. Rev. Lett. 116, 150502 (2016)

    ADS  Google Scholar 

  14. Bu, K., Singh, U., Fei, S.M., Pati, A.K., Wu, J.: Maximum relative entropy of coherence: an operational coherence measure. Phys. Rev. Lett. 119, 150405 (2017)

    ADS  MathSciNet  Google Scholar 

  15. Hu, M.L., Fan, H.: Relative quantum coherence, incompatibility, and quantum correlations of states. Phys. Rev. A 95, 052106 (2017)

    ADS  Google Scholar 

  16. Qi, X., Gao, T., Yan, F.: Measuring coherence with entanglement concurrence. J. Phys. A 50, 285301 (2017)

    MathSciNet  MATH  Google Scholar 

  17. Bu, K., Anand, N., Singh, U.: Asymmetry and coherence weight of quantum states. Phys. Rev. A 97, 032342 (2018)

    ADS  Google Scholar 

  18. de Vicente, J.I., Streltsov, A.: Genuine quantum coherence. J. Phys. A 50, 045301 (2017)

    ADS  MathSciNet  MATH  Google Scholar 

  19. Rastegin, A.E.: Quantum-coherence quantifiers based on the Tsallis relative \(\alpha \) entropies. Phys. Rev. A 93, 032136 (2016)

    ADS  Google Scholar 

  20. Rana, S., Parashar, P., Lewenstein, M.: Trace-distance measure of coherence. Phys. Rev. A 93, 012110 (2016)

    ADS  MathSciNet  Google Scholar 

  21. Shao, L.H., Xi, Z., Fan, H., Li, Y.: Fidelity and trace-norm distances for quantifying coherence. Phys. Rev. A 91, 042120 (2015)

    ADS  Google Scholar 

  22. Yao, Y., Dong, G.H., Ge, L., Li, M., Sun, C.P.: Maximal coherence in a generic basis. Phys. Rev. A 94, 062339 (2016)

    ADS  Google Scholar 

  23. Hu, M.L., Shen, S.Q., Fan, H.: Maximum coherence in the optimal basis. Phys. Rev. A 96, 052309 (2017)

    ADS  Google Scholar 

  24. Yu, C.S., Yang, S.R., Guo, B.Q.: Total quantum coherence and its applications. Quantum Inf. Process. 15, 3773 (2016)

    ADS  MathSciNet  MATH  Google Scholar 

  25. Streltsov, A., Kampermann, H., Wölk, S., Gessner, M., Bruß, D.: Maximal coherence and the resource theory of purity. New J. Phys. 20, 053058 (2018)

    ADS  MathSciNet  Google Scholar 

  26. Chitambar, E., Streltsov, A., Rana, S., Bera, M.N., Adesso, G., Lewenstein, M.: Assisted distillation of quantum coherence. Phys. Rev. Lett. 116, 070402 (2016)

    ADS  Google Scholar 

  27. Regula, B., Fang, K., Wang, X., Adesso, G.: One-shot coherence distillation. Phys. Rev. Lett. 121, 010401 (2018)

    ADS  Google Scholar 

  28. Fang, K., Wang, X., Lami, L., Regula, B., Adesso, G.: Probabilistic distillation of quantum coherence. Phys. Rev. Lett. 121, 070404 (2018)

    ADS  MathSciNet  Google Scholar 

  29. Liu, C.L., Zhou, D.L.: Catalyst-assisted probabilistic coherence distillation for mixed states. Phys. Rev. A 101, 012313 (2020)

    ADS  Google Scholar 

  30. Cheng, S., Hall, M.J.W.: Complementarity relations for quantum coherence. Phys. Rev. A 92, 042101 (2015)

    ADS  Google Scholar 

  31. Singh, U., Pati, A.K., Bera, M.N.: Uncertainty relations for quantum coherence. Mathematics 4, 47 (2016)

    MATH  Google Scholar 

  32. Yuan, X., Bai, G., Peng, T., Ma, X.: Quantum uncertainty relation using coherence. Phys. Rev. A 96, 032313 (2017)

    ADS  MathSciNet  Google Scholar 

  33. Singh, U., Bera, M.N., Dhar, H.S., Pati, A.K.: Maximally coherent mixed states: complementarity between maximal coherence and mixedness. Phys. Rev. A 91, 052115 (2015)

    ADS  Google Scholar 

  34. Bera, M.N., Qureshi, T., Siddiqui, M.A., Pati, A.K.: Duality of quantum coherence and path distinguishability. Phys. Rev. A 92, 012118 (2015)

    ADS  Google Scholar 

  35. Bagan, E., Bergou, J.A., Cottrell, S.S., Hillery, M.: Relations between coherence and path information. Phys. Rev. Lett. 116, 160406 (2016)

    ADS  Google Scholar 

  36. Tan, K.C., Kwon, H., Park, C.Y., Jeong, H.: Unified view of quantum correlations and quantum coherence. Phys. Rev. A 94, 022329 (2016)

    ADS  Google Scholar 

  37. Yao, Y., Xiao, X., Ge, L., Sun, C.P.: Quantum coherence in multipartite systems. Phys. Rev. A 92, 022112 (2015)

    ADS  Google Scholar 

  38. Zhang, J., Yang, S.R., Zhang, Y., Yu, C.S.: The classical correlation limits the ability of the measurement-induced average coherence. Sci. Rep. 7, 45598 (2017)

    ADS  Google Scholar 

  39. Hu, X., Fan, H.: Extracting quantum coherence via steering. Sci. Rep. 6, 34380 (2016)

    ADS  Google Scholar 

  40. Hu, X., Milne, A., Zhang, B., Fan, H.: Quantum coherence of steered states. Sci. Rep. 6, 19365 (2015)

    ADS  Google Scholar 

  41. Mondal, D., Pramanik, T., Pati, A.K.: Nonlocal advantage of quantum coherence. Phys. Rev. A 95, 010301 (2017)

    ADS  MathSciNet  Google Scholar 

  42. Hu, M.L., Fan, H.: Nonlocal advantage of quantum coherence in high-dimensional states. Phys. Rev. A 98, 022312 (2018)

    ADS  Google Scholar 

  43. Hu, M.L., Wang, X.M., Fan, H.: Hierarchy of the nonlocal advantage of quantum coherence and Bell nonlocality. Phys. Rev. A 98, 032317 (2018)

    ADS  Google Scholar 

  44. Datta, S., Majumdar, A.S.: Sharing of nonlocal advantage of quantum coherence by sequential observers. Phys. Rev. A 98, 042311 (2018)

    ADS  Google Scholar 

  45. Xie, Y.X., Gao, Y.Y.: Nonlocal advantage of quantum coherence in the Heisenberg XY model. Laser Phys. Lett. 16, 045202 (2019)

    ADS  Google Scholar 

  46. Xie, Y.X., Gao, Y.Y.: Impurity-assisted control of the nonlocal advantage of quantum coherence in the Heisenberg model. Laser Phys. Lett. 16, 075201 (2019)

    ADS  Google Scholar 

  47. Xie, Y.X., Zhang, Y.H.: Nonlocal advantage of quantum coherence in the spin-1/2 and spin-1 Heisenberg XXZ models. Laser Phys. Lett. 17, 035206 (2020)

    ADS  Google Scholar 

  48. Carvalho, A.R.R., Mintert, F., Buchleitner, A.: Decoherence and multipartite entanglement. Phys. Rev. Lett. 93, 230501 (2004)

    ADS  Google Scholar 

  49. Lee, B., Witzel, W.M., Sarma, S.D.: Universal pulse sequence to minimize spin dephasing in the central spin decoherence problem. Phys. Rev. Lett. 100, 160505 (2008)

    ADS  Google Scholar 

  50. Hu, M.L.: Disentanglement, Bell-nonlocality violation and teleportation capacity of the decaying tripartite states. Ann. Phys. (N.Y.) 327, 2332 (2012)

    ADS  MATH  Google Scholar 

  51. Mazzola, L., Piilo, J., Maniscalco, S.: Sudden transition between classical and quantum decoherence. Phys. Rev. Lett. 104, 200401 (2010)

    ADS  MathSciNet  Google Scholar 

  52. Werlang, T., Souza, S., Fanchini, F.F., Villas Boas, C.J.: Robustness of quantum discord to sudden death. Phys. Rev. A 80, 024103 (2009)

    ADS  Google Scholar 

  53. Maziero, J., Céleri, L.C., Serra, R.M., Vedral, V.: Classical and quantum correlations under decoherence. Phys. Rev. A 80, 044102 (2009)

    ADS  MathSciNet  Google Scholar 

  54. Wang, B., Xu, Z.Y., Chen, Z.Q., Feng, M.: Non-Markovian effect on the quantum discord. Phys. Rev. A 81, 014101 (2010)

    ADS  Google Scholar 

  55. Hu, M.L., Fan, H.: Robustness of quantum correlations against decoherence. Ann. Phys. (N.Y.) 327, 851 (2012)

    ADS  MATH  Google Scholar 

  56. Hu, M.L., Fan, H.: Evolution equation for geometric quantum correlation measures. Phys. Rev. A 91, 052311 (2015)

    ADS  Google Scholar 

  57. Hu, M.L., Tian, D.P.: Preservation of the geometric quantum discord in noisy environments. Ann. Phys. (N.Y.) 343, 132 (2014)

    ADS  MathSciNet  MATH  Google Scholar 

  58. Hu, M.L., Fan, H.: Dynamics of entropic measurement-induced nonlocality in structured reservoirs. Ann. Phys. (N.Y.) 327, 2343 (2012)

    ADS  MATH  Google Scholar 

  59. Hu, M.L., Fan, H.: Measurement-induced nonlocality based on the trace norm. New J. Phys. 17, 033004 (2015)

    ADS  Google Scholar 

  60. Li, Z., Xie, Y.X.: Steady-state measurement-induced nonlocality in thermal reservoir. Laser Phys. Lett. 15, 065208 (2018)

    ADS  Google Scholar 

  61. Bromley, T.R., Cianciaruso, M., Adesso, G.: Frozen quantum coherence. Phys. Rev. Lett. 114, 210401 (2015)

    ADS  Google Scholar 

  62. Yu, X.D., Zhang, D.J., Liu, C.L., Tong, D.M.: Measure-independent freezing of quantum coherence. Phys. Rev. A 93, 060303 (2016)

    ADS  Google Scholar 

  63. Silva, I.A., Souza, A.M., Bromley, T.R., Cianciaruso, M., Marx, R., Sarthour, R.S., Oliveira, I.S., Franco, R.L., Glaser, S.J., deAzevedo, E.R., Soares-Pinto, D.O., Adesso, G.: Observation of time-invariant coherence in a nuclear magnetic resonance quantum simulator. Phys. Rev. Lett. 117, 160402 (2016)

    ADS  Google Scholar 

  64. Zhang, A., Zhang, K., Zhou, L., Zhang, W.: Frozen condition of quantum coherence for atoms on a stationary trajectory. Phys. Rev. Lett. 121, 073602 (2018)

    ADS  Google Scholar 

  65. Hu, M.L., Fan, H.: Evolution equation for quantum coherence. Sci. Rep. 6, 29260 (2016)

    ADS  Google Scholar 

  66. Hu, M., Zhou, W.: Enhancing two-qubit quantum coherence in a correlated dephasing channel. Laser Phys. Lett. 16, 045201 (2019)

    ADS  Google Scholar 

  67. Liu, X.B., Tian, Z.H., Wang, J.C., Jing, J.L.: Protecting quantum coherence of two-level atoms from vacuum fluctuations of electromagnetic field. Ann. Phys. (N.Y.) 366, 102 (2016)

    ADS  MathSciNet  MATH  Google Scholar 

  68. Guarnieri, G., Kolář, M., Filip, R.: Steady-state coherences by composite system-bath interactions. Phys. Rev. Lett. 121, 070401 (2018)

    ADS  Google Scholar 

  69. Mukhopadhyay, C.: Generating steady quantum coherence and magic through an autonomous. Phys. Rev. A 98, 012102 (2018)

    ADS  Google Scholar 

  70. Hu, M.L., Fan, H.: Quantum coherence of multiqubit states in correlated noisy channels. Sci. China-Phys. Mech. Astron. 63, 230322 (2020)

    ADS  Google Scholar 

  71. Girolami, D.: Observable measure of quantum coherence in finite dimensional systems. Phys. Rev. Lett. 113, 170401 (2014)

    ADS  Google Scholar 

  72. Wigner, E.P., Yanase, M.M.: Information contents of distributions. Proc. Natl. Acad. Sci. U.S.A. 49, 910 (1963)

    ADS  MathSciNet  MATH  Google Scholar 

  73. Du, S., Bai, Z.: The Wigner–Yanase information can increase under phase sensitive incoherent operations. Ann. Phys. (N.Y.) 359, 136 (2015)

    MathSciNet  MATH  Google Scholar 

  74. Marvian, I., Spekkens, R.W.: Extending Noether’s theorem by quantifying the asymmetry of quantum states. Nat. Commun. 5, 3821 (2014)

    ADS  Google Scholar 

  75. Marvian, I., Spekkens, R.W., Zanardi, P.: Quantum speed limits, coherence, and asymmetry. Phys. Rev. A 93, 052331 (2016)

    ADS  Google Scholar 

  76. Marvian, I., Spekkens, R.W.: How to quantify coherence: distinguishing speakable and unspeakable notions. Phys. Rev. A 94, 052324 (2016)

    ADS  Google Scholar 

  77. Wooters, W.K.: Quantum mechanics without probability amplitudes. Found. Phys. 16, 391 (1986)

    ADS  MathSciNet  Google Scholar 

  78. Wooters, W.K., Fields, B.D.: Optimal state-determination by mutually unbiased measurements. Ann. Phys. (N.Y.) 191, 363 (1989)

    ADS  MathSciNet  Google Scholar 

  79. Durt, T., Englert, B.G., Bengtsson, I., Życzkowski, K.: On mutually unbiased basis. Int. J. Quantum Inf. 8, 535 (2010)

    MATH  Google Scholar 

  80. Breuer, H.P., Petruccione, F.: The Theory of Open Quantum Systems. Oxford University Press, Oxford (2001)

    MATH  Google Scholar 

  81. Kraus, K.: States Effects and Operations. Springer-Verlag, Berlin (1983)

    MATH  Google Scholar 

  82. Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2000)

    MATH  Google Scholar 

  83. Caruso, F., Giovannetti, V., Lupo, C., Mancini, S.: Quantum channels and memory effects. Rev. Mod. Phys. 86, 1203 (2014)

    ADS  Google Scholar 

  84. Macchiavello, C., Palma, G.M.: Entanglement-enhanced information transmission over a quantum channel with correlated noise. Phys. Rev. A 65, 050301 (2002)

    ADS  Google Scholar 

  85. Addis, C., Karpat, G., Macchiavello, C., Maniscalco, S.: Dynamical memory effects in correlated quantum channels. Phys. Rev. A 94, 032121 (2016)

    ADS  Google Scholar 

  86. Karpat, G.: Entropic uncertainty relation under correlated dephasing channels. Can. J. Phys. 96, 700 (2018)

    ADS  Google Scholar 

  87. Hu, M.L., Wang, H.F.: Protecting quantum Fisher information in correlated quantum channels. Ann. Phys. (Berlin) 532, 1900378 (2020)

    ADS  MathSciNet  Google Scholar 

  88. Daffer, S., Wodkiewicz, K., Cresser, J.D., McIver, J.K.: Depolarizing channel as a completely positive map with memory. Phys. Rev. A 70, 010304 (2004)

    ADS  Google Scholar 

  89. D’Arrigo, A., Benenti, G., Falci, G.: Quantum capacity of dephasing channels with memory. New J. Phys. 9, 310 (2007)

    ADS  Google Scholar 

  90. Benenti, G., D’Arrigo, A., Falci, G.: Enhancement of transmission rates in quantum memory channels with damping. Phys. Rev. Lett. 103, 020502 (2009)

    ADS  Google Scholar 

  91. D’Arrigo, A., Benenti, G., Falci, G.: Hamiltonian models for quantum memory channel. Int. J. Quantum Inf. 9, 625 (2011)

    MathSciNet  MATH  Google Scholar 

  92. D’Arrigo, A., Benenti, G., Falci, G.: Transmission of classical and quantum information through a quantum memory channel with damping. Eur. Phys. J. D 66, 147 (2012)

    ADS  Google Scholar 

  93. Wootters, W.K.: Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245 (1998)

    ADS  MATH  Google Scholar 

  94. Giovannetti, V., Palma, G.M.: Master equations for correlated quantum channels. Phys. Rev. Lett. 108, 040401 (2012)

    ADS  Google Scholar 

  95. Plenio, M.B., Virmani, S.: Spin chains and channels with memory. Phys. Rev. Lett. 99, 120504 (2007)

    ADS  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 11675129).

Author information

Authors and Affiliations

  1. School of Science, Xi’an University of Posts and Telecommunications, Xi’an, 710121, China

    Yu-Xia Xie & Zhi-Yong Qin

Authors
  1. Yu-Xia Xie
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Zhi-Yong Qin
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yu-Xia Xie.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xie, YX., Qin, ZY. Enhancing nonlocal advantage of quantum coherence in correlated quantum channels. Quantum Inf Process 19, 375 (2020). https://doi.org/10.1007/s11128-020-02870-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-020-02870-8

Keywords