Skip to main content

Advertisement

Springer Nature Link
Log in

Quantum coherence for an atom interacting with an electromagnetic field in the background of cosmic string spacetime

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

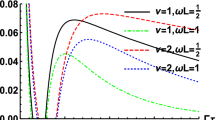
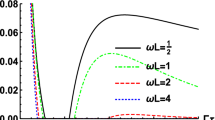
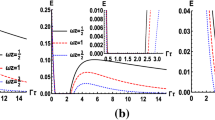
We investigate the behaviors of quantum coherence (QC) for an atom coupled to the fluctuating electromagnetic field under the cosmic string spacetime. It is found that vacuum fluctuation, atomic polarization and nontrivial spacetime topology affect the QC behaviors. When deficit angle parameter \(\nu =1\) and atom is far away from the string, the results restore to that of free Minkowski spacetime. When atom lies in the string and is transversely polarizable, the atom seems like a closed system, and QC completely is not affected by the electromagnetic fluctuation. For nonzero atom–string distance, QC presents oscillatory behaviors as atom–string distance changes, and larger deficit angle parameter causes more prominent oscillation. In a sense, the string can protect the QC to some extent, which is similar to the boundary effect in Minkowski spacetime. Besides, this atom eventually evolves to an incoherent state, which does not appear to be related to the initial state and other various parameters; this means QC cannot keep for long evolution time in the cosmic string spacetime. In principle, atomic polarization, atom–string distance and deficit angle parameter provide us more freedom to steer the QC behaviors, which might be useful to sense various cosmic string spacetime and distinguish the cosmic string spacetime from Minkowski spacetime.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Narasimhachar, V., Gour, G.: Low-temperature thermodynamics with quantum coherence. Nat. Commun. 6, 7689 (2015)

    Article  ADS  Google Scholar 

  2. Lostaglio, M., Jennings, D., Rudolph, T.: Description of quantum coherence in thermodynamic processes requires constraints beyond free energy. Nat. Commun. 6, 6383 (2015)

    Article  ADS  Google Scholar 

  3. Engel, G.S., Calhoun, T.R., Read, E.L., Ahn, T.-K., Manc̆al, T., Cheng, Y.-C., Blakenship, R.E., Fleming, G.R.: Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature (London) 446, 782 (2007)

  4. Lloyd, S.: Quantum coherence in biological systems. J. Phys: Conf. Ser. 302, 012037 (2011)

    Google Scholar 

  5. Lambert, N., Chen, Y.-N., Cheng, Y.-C., Li, C.-M., Chen, G.-Y., Nori, F.: Quantum biology. Nat. Phys. 9, 10 (2013)

    Article  Google Scholar 

  6. Joo, J., Munro, W.J., Spiller, T.P.: Quantum metrology with entangled coherent states. Phys. Rev. Lett. 107, 083601 (2011)

    Article  ADS  Google Scholar 

  7. Giovannetti, V., Lloyd, S., Maccone, L.: Advances in quantum metrology. Nat. Photonics 5, 222 (2011)

    Article  ADS  Google Scholar 

  8. Ma, J., Zhou, Y., Yuan, X., Ma, X.: Operational interpretation of coherence in quantum key distribution. Phys. Rev. A 99, 062325 (2019)

    Article  ADS  Google Scholar 

  9. Streltsov, A., Singh, U., Dhar, H.S., Bera, M.N., Adesso, G.: Measuring quantum coherence with entanglement. Phys. Rev. Lett. 115, 020403 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  10. Yao, Y., Xiao, X., Ge, L., Sun, C.P.: Quantum coherence in multipartite systems. Phys. Rev. A 92, 022112 (2015)

    Article  ADS  Google Scholar 

  11. Ma, J.J., Yadin, B., Girolami, D., Vedral, V., Gu, M.: Converting coherence to quantum correlations. Phys. Rev. Lett. 116, 160407 (2016)

    Article  ADS  Google Scholar 

  12. Tan, K.C., Jeong, H.: Entanglement as the symmetric portion of correlated coherence. Phys. Rev. Lett. 121, 220401 (2018)

    Article  ADS  Google Scholar 

  13. Baumgratz, T., Cramer, M., Plenio, M.B.: Quantifying coherence. Phys. Rev. Lett. 113, 140401 (2014)

    Article  ADS  Google Scholar 

  14. Liu, X.B., Tian, Z.H., Wang, J.C., Jing, J.L.: Inhibiting decoherence of two-level atom in thermal bath by presence of boundaries. Quantum Inf. Process. 15, 3677 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  15. Huang, Z.M., Situ, H.Z.: Dynamics of quantum correlation and coherence for two atoms coupled with a bath of fluctuating massless scalar field. Ann. Phys. 377, 484 (2017)

    Article  ADS  Google Scholar 

  16. Huang, Z.M., Zhang, W.: Quantum coherence behaviors for a uniformly accelerated atom immersed in fluctuating vacuum electromagnetic field with a boundary. Braz. J. Phys. 49, 161 (2019)

    Article  ADS  Google Scholar 

  17. Huang, Z.M.: Dynamics of quantum correlation and coherence in de Sitter universe. Quantum Inf. Process. 16, 207 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  18. Velenkin, A., Shellard, E.P.S.: Cosmic Strings and Other Topological Defects. Cambridge University Press, Cambridge (1994)

    MATH  Google Scholar 

  19. Vilenkin, A.: Cosmic strings as gravitational lenses. Astrophys. J. 282, L51 (1984)

    Article  ADS  MathSciNet  Google Scholar 

  20. Gott, J.R.: Gravitational lensing effects of vacuum strings-exact solutions. Astrophys. J. 288, 422 (1985)

    Article  ADS  MathSciNet  Google Scholar 

  21. Ford, L.H., Vilenkin, A.: A gravitational analogue of the AharonovCBohm effect. J. Phys. A: Math. Gen. 14, 2353 (1981)

    Article  ADS  Google Scholar 

  22. Bezerra, V.B.: Gravitational analogs of the Aharonov–Bohm effect. J. Math. Phys. 30, 2895 (1989)

    Article  ADS  MathSciNet  Google Scholar 

  23. Audretsch, J., Economou, A.: Conical bremsstrahlung in a cosmic-string spacetime. Phys. Rev. D 44, 3774 (1991)

    Article  ADS  Google Scholar 

  24. Saharian, A.A., Kotanjyan, A.S.: Repulsive Casimir–Polder forces from cosmic strings. Eur. Phys. J. C 71, 1765 (2011)

    Article  ADS  Google Scholar 

  25. Cai, H., Yu, H., Zhou, W.: Spontaneous excitation of a static atom in a thermal bath in cosmic string spacetime. Phys. Rev. D 92, 084062 (2015)

    Article  ADS  Google Scholar 

  26. Zhou, W., Yu, H.: Spontaneous excitation of a uniformly accelerated atom in the cosmic string spacetime. Phys. Rev. D 93, 084028 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  27. Cai, H., Ren, Z.: Radiative processes of two entangled atoms in cosmic string spacetime. Class. Quantum Grav. 35, 025016 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  28. Bakke, K., Ribeiro, L.R., Furtado, C., Nascimento, J.R.: Landau quantization for a neutral particle in the presence of topological defects. Phys. Rev. D 79, 024008 (2009)

    Article  ADS  Google Scholar 

  29. Figueiredo Medeiros, E.R., Bezerra de Mello, E.R.: Relativistic quantum dynamics of a charged particle in cosmic string spacetime in the presence of magnetic field and scalar potential. Eur. Phys. J. C 72, 2051 (2012)

    Article  ADS  Google Scholar 

  30. Bakke, K., Nascimento, J.R., Furtado, C.: Geometric phase for a neutral particle in the presence of a topological defect. Phys. Rev. D 78, 064012 (2008)

    Article  ADS  Google Scholar 

  31. Cai, H., Ren, Z.: Geometric phase for a static two-level atom in cosmic string spacetime. Class. Quantum Grav. 35, 105014 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  32. Bezerra de Mello, E.R., Saharian, A.A., Kh Grigoryan, A.: Casimir effect for parallel metallic plates in cosmic string spacetime. J. Phys. A: Math. Theor. 45, 374011 (2012)

    Article  MathSciNet  Google Scholar 

  33. Gorini, V., Kossakowski, A., Surdarshan, E.C.G.: Completely positive dynamical semigroups of N-level systems. J. Math. Phys. 17, 821 (1976)

    Article  ADS  MathSciNet  Google Scholar 

  34. Lindblad, G.: On the generators of quantum dynamical semigroups. Commun. Math. Phys. 48, 119 (1976)

    Article  ADS  MathSciNet  Google Scholar 

  35. Breuer, H.-P., Petruccione, F.: The Theory of Open Quantum Systems. Oxford University Press, Oxford (2002)

    MATH  Google Scholar 

  36. Andrews, G.E., Askey, R., Roy, R.: Special Functions. Cambridge University Press, Cambridge (1999)

    Book  Google Scholar 

  37. Jin, Y., Yu, H.W.: Electromagnetic shielding in quantum metrology. Phys. Rev. A 91, 022120 (2015)

    Article  ADS  Google Scholar 

  38. Yu, S., et al.: Experimental realization of self-guided quantum coherence freezing. Phys. Rev. A 96, 062324 (2017)

    Article  ADS  Google Scholar 

  39. Zheng, W., et al.: Experimental demonstration of observability and operability of robustness of coherence. Phys. Rev. Lett. 120, 230504 (2018)

    Article  ADS  Google Scholar 

  40. Ding, Z.Y., et al.: Experimental investigation of the nonlocal advantage of quantum coherence. Phys. Rev. A 100, 022308 (2019)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work is supported by the Innovation Project of Department of Education of Guangdong Province of China (2019KTSCX188).

Author information

Authors and Affiliations

  1. School of Economics and Management, Wuyi University, Jiangmen, 529020, China

    Zhiming Huang

Authors
  1. Zhiming Huang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Zhiming Huang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Huang, Z. Quantum coherence for an atom interacting with an electromagnetic field in the background of cosmic string spacetime. Quantum Inf Process 19, 370 (2020). https://doi.org/10.1007/s11128-020-02878-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-020-02878-0

Keywords