Quantum Stackelberg–Bertrand duopoly

Abstract

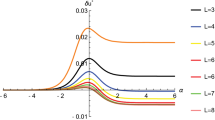
We apply Li et al.’s “minimal” quantization rules (Phys. Lett. A 306, 73, 2002) to investigate the quantum version of the Stackelberg–Bertrand duopoly, especially how the quantum entanglement affects the second-mover advantage in the Stackelberg–Bertrand duopoly. It is found that positive quantum entanglement is more favourable to the profit of the leader and destroys the second-mover advantage.

Appendix

To derive the Nash equilibrium shown in Eqs. (5) and (6) from Eqs. (3) and (4), we first determine the reaction function of the follower who is supposed to react optimally to the price chosen by the leader and maximizes his or her profit. This can be achieved by requiring

$$\begin{aligned} \frac{\partial {u_{F}}\left( p_{L},p_{F}\right) }{\partial {p_{F}}} =0\implies {\overline{p}}_{F}=\frac{1}{2}\left( a+c+bp_{L}\right) . \end{aligned}$$

(A.1)

Here, ${\overline{p}}_{F}$ is the reaction function of the follower. For different values of $p_{L}$, the follower will optimize his or her profit with the price ${\overline{p}}_{F}$. Subsequently, against the optimal response of the follower, the leader maximizes his or her profit as follows:

$$\begin{aligned} \frac{\partial {u_{L}\left( p_{L},{\overline{p}}_{F}\right) }}{\partial {p_{L}} }=0\implies p_{L}^{*}=\frac{a\left( 2+b\right) +c\left( 2+b-b^{2}\right) }{2\left( 2-b^{2}\right) } . \end{aligned}$$

(A.2)

Substituting $p_{L}^{*}$ into Eq. (A.1), we obtain

$$\begin{aligned} p_{F}^{*}=\frac{a\left( 4+2b-b^{2}\right) +c\left( 4+2b-b^{2}-b^{3}\right) }{4\left( 2-b^{2}\right) } . \end{aligned}$$

(A.3)

With these optimal prices their profits are then given by Eqs. (7) and (8). Moreover, their counterparts in the quantized game shown in Eqs. (18)–(21) can be derived in a similar manner.

Finally, to obtain the asymptotic limits in Eqs. (22)–(25), one can first rewrite the expressions in Eqs. (20) and (21) in terms of $\tanh \gamma$, and then apply the limit $\tanh \gamma \longrightarrow \pm 1$ as $\gamma \longrightarrow \pm \infty$.