Dynamical characteristic of entropic uncertainty relation in the long-range Ising model with an arbitrary magnetic field

Abstract

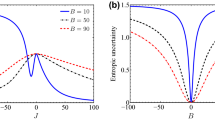
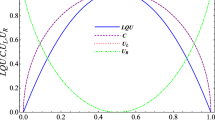
In this work, we explore the quantum-memory-assisted entropic uncertainty relation (QMA-EUR) and the entanglement concurrence for the long-range Ising (LRI) model in the presence of an arbitrary magnetic field. The long-range interaction is considered as type of the Calogero–Moser interaction that is inversely proportional to the square of the distance between the spins. It is shown that the measurement’s uncertainty and the entanglement concurrence are extremely sensitive to the effects of the distance between spins, the magnitude, and the direction of the external magnetic field. The evaluation of the QMA-EUR is fully related to the entanglement concurrence in case of the LRI model. At larger distances between the spins, there is inflation in the measuring uncertainty due to the fragile entanglement between them. The evolutions of the entanglement and the uncertainty show only similar dynamical characteristics in antiferromagnetic and ferromagnetic frames when the magnetic field is perpendicular to the z-axis.

Appendix A

As mentioned above, the post-measurement state takes the form

$$\begin{aligned} \rho _{XB} = \sum \nolimits _x {(\left| {\psi _x } \right\rangle \left\langle {\psi _x } \right| \otimes \mathbf{{I}})} \rho _{AB} (\left| {\psi _x } \right\rangle \left\langle {\psi _x } \right| \otimes \mathbf{{I}}), \end{aligned}$$

(A1)

where $X \in \left\{ {P,Q} \right\}$ and , ${\left| {\psi _x } \right\rangle }$ are the eigenvectors of X. By replacing the incompatibility P and Q by the spin-1/2 operators $\sigma _x$ and $\sigma _z$, the post-measurement states, $\rho _{\sigma _x B}$ and $\rho _{\sigma _z B}$ and also the reduced density matrix $\rho _B$ of the quantum memory B can be derived as

$$\begin{aligned} \rho _{\sigma _x B}= & {} \left( {\begin{array}{*{20}c} {\frac{1}{4}} &{} \mathcal{K} &{} \mathcal{K} &{} {\frac{{\mathcal{G}_ - - \mathcal{L}_ - }}{2}} \\ \mathcal{K} &{} {\frac{1}{4}} &{} {\frac{{\mathcal{G}_ - - \mathcal{L}_ - }}{2}} &{} \mathcal{K} \\ \mathcal{K} &{} {\frac{{\mathcal{G}_ - - \mathcal{L}_ - }}{2}} &{} {\frac{1}{4}} &{} \mathcal{K} \\ {\frac{{\mathcal{G}_ - - \mathcal{L}_ - }}{2}} &{} \mathcal{K} &{} \mathcal{K} &{} {\frac{1}{4}} \\ \end{array}} \right) , \nonumber \\ \rho _{\sigma _z B}= & {} \left( {\begin{array}{*{20}c} {\mathcal{G}_ + } &{} \mathcal{K} &{} 0 &{} 0 \\ \mathcal{K} &{} {\mathcal{L}_ + } &{} 0 &{} 0 \\ 0 &{} 0 &{} {\mathcal{L}_ + } &{} \mathcal{K} \\ 0 &{} 0 &{} \mathcal{K} &{} {\mathcal{G}_ + } \\ \end{array}} \right) , \nonumber \\ \rho _B= & {} \left( {\begin{array}{*{20}c} {\frac{1}{2}} &{} {2\mathcal{K}} \\ {2\mathcal{K}} &{} {\frac{1}{2}} \\ \end{array}} \right) . \end{aligned}$$

(A2)

After some calculations one can get:

$$\begin{aligned} \mathcal{X}_{1,2}= & {} \frac{{\cosh \alpha _1 }}{Z} \pm 2\mathcal{K},\,\,\,\,\,\,\,\,\,\,\,\mathcal{X}_{3,4} = \frac{{\cosh \alpha _2 }}{Z}, \end{aligned}$$

(A3)

$$\begin{aligned} \mathcal{Z}_{1,2}= & {} \frac{{1 - 2\sqrt{\varpi }}}{4},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathcal{Z}_{3,4} = \frac{{1 + 2\sqrt{\varpi }}}{4}, \end{aligned}$$

(A4)

$$\begin{aligned} \mathcal{B}_{1}= & {} \frac{{1 - 4\mathcal{K}}}{2},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathcal{B}_{2} = \frac{{1 + 4\mathcal{K}}}{2}. \end{aligned}$$

(A5)

where $\mathcal{X}_i$, $\mathcal{Z}_i$ and $\mathcal{B}_i$ are the eigenvalues of ${\rho _{\sigma _x B} }$, ${\rho _{\sigma _z B} }$ and $\rho _B$, respectively, and $\varpi = \left( {\mathcal{G}_ + - \mathcal{L}_ + } \right) ^2 + 4\mathcal{K}^2$. On the other hand, the eigenvalues of the density matrix, Eq. (8), are

$$\begin{aligned} \mathcal{D}_{1,2} = \frac{{\exp \left( { \pm \alpha _1 } \right) }}{Z},\,\,\,\,\,\,\,\,\,\,\,\,\mathcal{D}_{3,4} = \frac{{\exp \left( { \pm \alpha _2 } \right) }}{Z}. \end{aligned}$$

(A6)

It is well known that for an arbitrary state, $\rho$, the von Neumann entropy can be expressed as $S(\rho ) = - \sum \nolimits _i \Omega _i \log _2 \Omega _i$ where $\Omega _i$ are the eigenvalues of $\rho$. Using this definition and the eigenvalues (A3–A6) one can deduce Eq. (10).