Abstract
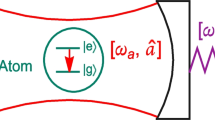
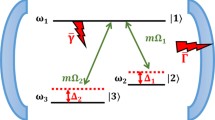
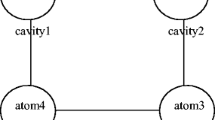
In this paper, we propose a theoretical scheme to study the dynamics of the geometric measure of quantum discord (GMQD) between two non-interacting qubits in a dissipative optomechanical system composed of two Fabry–Pérot cavities. In this system, each cavity contains a single-mode quantized radiation field which, in the rotating wave approximation, interacts with both mechanical resonator and two-level atom. In addition, the effects of dissipation are taken into account by considering cavity decay, losses of cavity mirror, and spontaneous emission from the atom. We start with the master equation approach and under some circumstances, we find a non-Hermitian Hamiltonian. Adopting this procedure yields the problem with an acceptable analytical solution. This means that all enough information in the study of the considered open quantum system is exactly obtained. Thereupon, we study the quantum correlations between the atoms with the help of the GMQD. It can be seen that the GMQD between two atoms can be controlled by the optomechanical coupling coefficient, the atom-field coupling strength and the dissipation parameters. Moreover, decreasing the coefficient of optomechanical coupling as well as reducing the strength of atom-field coupling improves the GMQD between two atoms. It is also mentioned that, taking the dissipation effects into account, we see that, as the time proceeds, the GMQD approaches to a stable value. In addition, eliminating the effect of spontaneous emission leads to a diminution in the amount of GMQD. Consequently, the quantum correlations between two atoms can be enhanced by considering the effect of spontaneous emission.





Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Feng, Z.B., Wang, H.L., Yan, R.Y.: Quantum state transfer between an optomechanical cavity and a diamond nuclear spin ensemble. Quantum Inf. Process. 15(8), 3151–3167 (2016)
Sete, E.A., Eleuch, H.: High-efficiency quantum state transfer and quantum memory using a mechanical oscillator. Phys. Rev. A 91, 032309 (2015)
Teh, R.Y., Kiesewetter, S., Reid, M.D., Drummond, P.D.: Simulation of an optomechanical quantum memory in the nonlinear regime. Phys. Rev. A 96, 013854 (2017)
Stannigel, K., Komar, P., Habraken, S.J.M., Bennett, S.D., Lukin, M.D., Zoller, P., Rabl, P.: Optomechanical quantum information processing with photons and phonons. Phys. Rev. Lett. 109, 013603 (2012)
Momenabadi, F.M., Baghshahi, H.R., Faghihi, M.J., Mirafzali, S.Y.: Stable entanglement in a quadripartite cavity optomechanics. Eur. Phys. J. Plus 136(1), 7 (2021)
Taylor, M.A., Janousek, J., Daria, V., Knittel, J., Hage, B., Bachor, H.A., Bowen, W.P.: Biological measurement beyond the quantum limit. Nat. Photonics 7(3), 229 (2013)
Abadie, J., Abbott, B.P., Abbott, R., Abbott, T.D., Abernathy, M., Adams, C., Adhikari, R., Affeldt, C., Allen, B., Allen, G., et al.: A gravitational wave observatory operating beyond the quantum shot-noise limit. Nat. Phys. 7(12), 962 (2011)
Salehi, M.J., Baghshahi, H.R., Mirafzali, S.Y.: Quantum correlation and squeezing dynamics of a dissipative nonlinear optomechanical oscillator: Heisenberg-Langevin approach. Eur. Phys. J. Plus 133(11), 471 (2018)
Lee, J.H., Suh, J., Seok, H.: Dissipation-driven nonclassical-state generation in optomechanics with squeezed light. Phys. Rev. A 98, 043821 (2018)
Nejad, A.A., Askari, H., Baghshahi, H.: Normal mode splitting in an optomechanical system: effects of coulomb and parametric interactions. J. Opt. Soc. Am. B 35(9), 2237–2243 (2018)
Aspelmeyer, M., Kippenberg, T.J., Marquardt, F.: Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014)
Brooks, D.W., Botter, T., Schreppler, S., Purdy, T.P., Brahms, N., Stamper-Kurn, D.M.: Non-classical light generated by quantum-noise-driven cavity optomechanics. Nature 488(7412), 476–480 (2012)
Metcalfe, M.: Applications of cavity optomechanics. Appl. Phys. Rev. 1(3), 031105 (2014)
Pirkkalainen, J.M., Cho, S., Massel, F., Tuorila, J., Heikkilä, T., Hakonen, P., Sillanpää, M.: Cavity optomechanics mediated by a quantum two-level system. Nat. Commun. 6(1), 1–6 (2015)
Liao, J.Q., Tian, L.: Macroscopic quantum superposition in cavity optomechanics. Phys. Rev. Lett. 116, 163602 (2016)
Wang, D.Y., Bai, C.H., Wang, H.F., Zhu, A.D., Zhang, S.: Steady-state mechanical squeezing in a hybrid atom-optomechanical system with a highly dissipative cavity. Sci. Rep. 6(1), 1–8 (2016)
Tan, H., Deng, W., Wu, Q., Li, G.: Steady-state light-mechanical quantum steerable correlations in cavity optomechanics. Phys. Rev. A 95, 053842 (2017)
Cripe, J., Aggarwal, N., Singh, R., Lanza, R., Libson, A., Yap, M..J., Cole, G..D., McClelland, D..E., Mavalvala, N., Corbitt, T.: Radiation-pressure-mediated control of an optomechanical cavity. Phys. Rev. A 97, 013827 (2018)
Liu, J.H., Zhang, Y.B., Yu, Y.F., Zhang, Z.M.: Photon-phonon squeezing and entanglement in a cavity optomechanical system with a flying atom. Front. Phys. 14(1), 12601 (2019)
Liao, Q., Xiao, X., Nie, W., Zhou, N.: Transparency and tunable slow-fast light in a hybrid cavity optomechanical system. Opt. Express 28(4), 5288–5305 (2020)
Yan, X.B., Cui, C.L., Gu, K.H., Tian, X.D., Fu, C.B., Wu, J.H.: Coherent perfect absorption, transmission, and synthesis in a double-cavity optomechanical system. Opt. Express 22(5), 4886–4895 (2014)
Guo, Y., Li, K., Nie, W., Li, Y.: Electromagnetically-induced-transparency-like ground-state cooling in a double-cavity optomechanical system. Phys. Rev. A 90, 053841 (2014)
El Qars, J., Daoud, M., Laamara, A.: Entanglement versus Gaussian quantum discord in a double-cavity opto-mechanical system. Int. J. Quantum Inf. 13(06), 1550041 (2015)
Yan, X.B., Jia, W., Li, Y., Wu, J.H., Li, X.L., Mu, H.W.: Optomechanically induced amplification and perfect transparency in double-cavity optomechanics. Front. Phys. 10(3), 351–357 (2015)
Huan, T., Zhou, R., Ian, H.: Dynamic entanglement transfer in a double-cavity optomechanical system. Phys. Rev. A 92, 022301 (2015)
Wang, D.Y., Bai, C.H., Wang, H.F., Zhu, A.D., Zhang, S.: Steady-state mechanical squeezing in a double-cavity optomechanical system. Sci. Rep. 6, 38559 (2016)
Chen, Z.X., Lin, Q., He, B., Lin, Z.Y.: Entanglement dynamics in double-cavity optomechanical systems. Opt. Express 25(15), 17237–17248 (2017)
Chao, S.L., Xiong, B., Zhou, L.: Generating a squeezed-coherent-cat state in a double-cavity optomechanical system. Ann. Phys. (Berlin) 531(11), 1900196 (2019)
Liao, Q.H., Dai, Y.Z., Nie, W.J., Liu, X., Liu, Y.C.: Cooling of mechanical resonator in a double-cavity system with two-level atomic ensemble. J. Phys. B: At., Mol. Opt. Phys. 53(8), 085402 (2020)
Yan, X.B., Lu, H.L., Gao, F., Yang, L.: Perfect optical nonreciprocity in a double-cavity optomechanical system. Front. Phys. 14(5), 52601 (2019)
Han, Y., Xue, L., Chen, B.: Generation of two-mode squeezing of mechanical oscillators in the multi-mode optomechanical systems. Quantum Inf. Process. 19(4), 1–12 (2020)
Huang, S., Agarwal, G.S.: Robust force sensing for a free particle in a dissipative optomechanical system with a parametric amplifier. Phys. Rev. A 95, 023844 (2017)
Liao, C.G., Xie, H., Shang, X., Chen, Z.H., Lin, X.M.: Enhancement of steady-state bosonic squeezing and entanglement in a dissipative optomechanical system. Opt. Express 26(11), 13783–13799 (2018)
Mehmood, A., Qamar, S., Qamar, S.: Effects of laser phase fluctuation on force sensing for a free particle in a dissipative optomechanical system. Phys. Rev. A 98, 053841 (2018)
Huang, S., Chen, A.: Improving the cooling of a mechanical oscillator in a dissipative optomechanical system with an optical parametric amplifier. Phys. Rev. A 98, 063818 (2018)
Liao, C.G., Chen, R.X., Xie, H., He, M.Y., Lin, X.M.: Quantum synchronization and correlations of two mechanical resonators in a dissipative optomechanical system. Phys. Rev. A 99, 033818 (2019)
de Moraes Neto, G.D., Montenegro, V., Teizen, V.F., Vernek, E.: Dissipative phonon-Fock-state production in strong nonlinear optomechanics. Phys. Rev. A 99, 043836 (2019)
Nadiki, M.H., Tavassoly, M.: The amplitude of the cavity pump field and dissipation effects on the entanglement dynamics and statistical properties of an optomechanical system. Opt. Commun. 452, 31–39 (2019)
Xiong, B., Li, X., Chao, S.L., Yang, Z., Peng, R., Zhou, L.: Strong squeezing of duffing oscillator in a highly dissipative optomechanical cavity system. Ann. Phys. 532(4), 1900596 (2020)
Vitali, D., Gigan, S., Ferreira, A., Böhm, H., Tombesi, P., Guerreiro, A., Vedral, V., Zeilinger, A., Aspelmeyer, M.: Optomechanical entanglement between a movable mirror and a cavity field. Phys. Rev. Lett. 98(3), 030405 (2007)
Wang, Y.D., Clerk, A.A.: Reservoir-engineered entanglement in optomechanical systems. Physical review letters 110(25), 253601 (2013)
Wang, G., Huang, L., Lai, Y.C., Grebogi, C.: Nonlinear dynamics and quantum entanglement in optomechanical systems. Physical review letters 112(11), 110406 (2014)
Cheng, J., Zhang, W.Z., Zhou, L., Zhang, W.: Preservation macroscopic entanglement of optomechanical systems in non-markovian environment. Sci. Rep. 6(1), 1–8 (2016)
Bai, C.H., Wang, D.Y., Zhang, S., Liu, S., Wang, H.F.: Modulation-based atom-mirror entanglement and mechanical squeezing in an unresolved-sideband optomechanical system. Ann. Phys. (Berlin) 531(7), 1800271 (2019)
Hu, C.S., Liu, Z.Q., Liu, Y., Shen, L.T., Wu, H., Zheng, S.B.: Entanglement beating in a cavity optomechanical system under two-field driving. Phys. Rev. A 101(3), 033810 (2020)
Jennewein, T., Simon, C., Weihs, G., Weinfurter, H., Zeilinger, A.: Quantum cryptography with entangled photons. Phys. Rev. Lett. 84, 4729–4732 (2000)
Yang, X., Bai, M.q., Mo, Z.w., Xiang, Y.: Bidirectional and cyclic quantum dense coding in a high-dimension system. Quantum Inf. Process. 19(2), 43 (2020)
Anagha, M., Mohan, A., Muruganandan, T., Behera, B..K., Panigrahi, P..K.: A new scheme of quantum teleportation using highly entangled brown et al. state: an IBM quantum experience. Quantum Inf. Process 19(5), 1–12 (2020)
D’ambrosio, V., Spagnolo, N., Del Re, L., Slussarenko, S., Li, Y., Kwek, L.C., Marrucci, L., Walborn, S.P., Aolita, L., Sciarrino, F.: Photonic polarization gears for ultra-sensitive angular measurements. Nat. Commun. 4(1), 1–8 (2013)
Koike, S., Takahashi, H., Yonezawa, H., Takei, N., Braunstein, S.L., Aoki, T., Furusawa, A.: Demonstration of quantum telecloning of optical coherent states. Phys. Rev. Lett. 96, 060504 (2006)
Ollivier, H., Zurek, W.H.: Quantum discord: A measure of the quantumness of correlations. Phys. Rev. Lett. 88, 017901 (2001)
Henderson, L., Vedral, V.: Classical, quantum and total correlations. J. Phys. A: Math. Gen. 34(35), 6899 (2001)
Ferraro, A., Aolita, L., Cavalcanti, D., Cucchietti, F.M., Acín, A.: Almost all quantum states have nonclassical correlations. Phys. Rev. A 81, 052318 (2010)
Rana, S., Parashar, P.: Entanglement is not a lower bound for geometric discord. Phys. Rev. A 86, 030302 (2012)
Dakić, B., Vedral, V., Brukner, I..C..V.: Necessary and sufficient condition for nonzero quantum discord. Phys. Rev. Lett. 105, 190502 (2010)
Dakić, B., Lipp, Y.O., Ma, X., Ringbauer, M., Kropatschek, S., Barz, S., Paterek, T., Vedral, V., Zeilinger, A., Brukner, Č, et al.: Quantum discord as resource for remote state preparation. Nat. Phys. 8(9), 666–670 (2012)
Tufarelli, T., Girolami, D., Vasile, R., Bose, S., Adesso, G.: Quantum resources for hybrid communication via qubit-oscillator states. Phys. Rev. A 86, 052326 (2012)
Chaves, R., de Melo, F.: Noisy one-way quantum computations: the role of correlations. Phys. Rev. A 84, 022324 (2011)
Yao, Y., Li, H.W., Zou, X.B., Huang, J.Z., Zhang, C.M., Yin, Z.Q., Chen, W., Guo, G.C., Han, Z.F.: Quantum discord in quantum random access codes and its connection to dimension witnesses. Phys. Rev. A 86, 062310 (2012)
Giampaolo, S.M., Streltsov, A., Roga, W., Bruß, D., Illuminati, F.: Quantifying nonclassicality: Global impact of local unitary evolutions. Phys. Rev. A 87, 012313 (2013)
Laha, P., Lakshmibala, S., Balakrishnan, V.: Nonclassical effects in optomechanics: dynamics and collapse of entanglement. J. Opt. Soc. Am. B 36(3), 575–584 (2019)
Barnett, S.M., Jeffers, J.: The damped Jaynes-Cummings model. J. Mod. Opt. 54(13–15), 2033–2048 (2007)
Di Fidio, C., Vogel, W., Khanbekyan, M., Welsch, D.G.: Photon emission by an atom in a lossy cavity. Phys. Rev. A 77, 043822 (2008)
Di Fidio, C., Vogel, W.: Entanglement signature in the mode structure of a single photon. Phys. Rev. A 79, 050303 (2009)
Di Fidio, C., Vogel, W.: Entanglement evolution in a cascaded system with losses. Physica E 42(3), 369–373 (2010)
Baghshahi, H.R., Tavassoly, M.K., Behjat, A.: Entanglement of a damped non-degenerate \(\diamond \)-type atom interacting nonlinearly with a single-mode cavity. Eur. Phys. J. Plus 131(4), 80 (2016)
Mohamed, A.B.A.: Bipartite non-classical correlations for a lossy two connected qubit-cavity systems: trace distance discord and Bell’s non-locality. Quantum Inf. Process. 17(4), 1–18 (2018)
Alqahtani, M.M.: Multiphoton process in cavity QED photons for implementing a three-qubit quantum gate operation. Quantum Inf. Process. 19(1), 1–15 (2020)
Liao, J.Q., Nori, F.: Photon blockade in quadratically coupled optomechanical systems. Phys. Rev. A 88, 023853 (2013)
Xie, H., Lin, G.W., Chen, X., Chen, Z.H., Lin, X.M.: Single-photon nonlinearities in a strongly driven optomechanical system with quadratic coupling. Phys. Rev. A 93, 063860 (2016)
Xie, H., Liao, C.G., Shang, X., Ye, M.Y., Lin, X.M.: Phonon blockade in a quadratically coupled optomechanical system. Phys. Rev. A 96, 013861 (2017)
Zhang, J.S., Li, M.C., Chen, A.X.: Enhancing quadratic optomechanical coupling via a nonlinear medium and lasers. Phys. Rev. A 99, 013843 (2019)
Wang, D.Y., Bai, C.H., Liu, S., Zhang, S., Wang, H.F.: Photon blockade in a double-cavity optomechanical system with nonreciprocal coupling. New J. Phys. 22(9), 093006 (2020)
Eleuch, H.: Photon statistics of light in semiconductor microcavities. J. Phys. B: At. Mol. Opt. Phys. 41(5), 055502 (2008)
Mohamed, A.B., Eleuch, H.: Non-classical effects in cavity QED containing a nonlinear optical medium and a quantum well: Entanglement and non-Gaussanity. Eur. Phys. J. D 69(8), 191 (2015)
Altintas, F.: Geometric measure of quantum discord in non-Markovian environments. Opt. Commun. 283(24), 5264–5268 (2010)
Lecocq, F., Teufel, J.D., Aumentado, J., Simmonds, R.W.: Resolving the vacuum fluctuations of an optomechanical system using an artificial atom. Nat. Phys. 11(8), 635–639 (2015)
Altintas, F., Eryigit, R.: Creation of quantum correlations between two atoms in a dissipative environment from an initial vacuum state. Phys. Lett. A 376(22), 1791–1796 (2012)
Altintas, F., Eryigit, R.: Dissipative dynamics of quantum correlations in the strong-coupling regime. Phys. Rev. A 87, 022124 (2013)
Gamel, O., James, D.F.V.: Time-averaged quantum dynamics and the validity of the effective hamiltonian model. Phys. Rev. A 82, 052106 (2010)
Acknowledgements
We gratefully thank the referees for their constructive comments that truly helped us to enhance the quality of the paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Proof of Eq. (3)
Proof of Eq. (3)
Here, we want to demonstrate how the effective Hamiltonian of the whole system, which is introduced in Eq. (3), can be obtained. To this end, first suppose that an interaction Hamiltonian could be written as follows
where N is the total number of different harmonic terms, which make up the interaction Hamiltonian, with oscillating frequency \( \omega _{n} > 0 \). Then, the effective Hamiltonian reduces to
in which \( \bar{\omega }_{mn}\) is the harmonic average of \(\omega _{m}\) and \(\omega _{n}\), defined as \(\frac{1}{\bar{\omega }_{mn}} = \frac{1}{2}(\frac{1}{\omega _{m}}+\frac{1}{\omega _{n}})\) [80]. Thus, by repeating the mentioned-above procedure for the present system, it is required to write the Hamiltonian in Eq. (1) in the interaction picture as
with \(\varDelta _{k}=\varOmega _{k}-\omega _{k}\) being the detuning parameter between the cavity field and the atom. Under the condition \(\varDelta _{k}=\omega _{km}\) [28, 31, 61], Eq. (19) gets the form
Comparing Eq. (17) with that of (20), one would be able to find the operators \( \hat{h}_{n} \), associated with the Hamiltonian (20), as \(\hat{h}_{1} = \lambda _{1} \hat{a}_{1} \hat{\sigma }_{+}^{(1)}\), \(\hat{h}_{2} = \lambda _{2} \hat{a}_{2} \hat{\sigma }_{+}^{(2)}\), \(\hat{h}_{3} = - G_{1} \hat{a}^\dagger _{1} \hat{a}_{1} \hat{b}_{1}\), and \(\hat{h}_{4} = - G_{2} \hat{a}^\dagger _{2} \hat{a}_{2} \hat{b}_{2}\) with \(\omega _{n} = \omega _{km}, i=1,2,3,4\). Applying Eq. (18) along with doing some manipulations, we arrive at the effective Hamiltonian of the whole system introduced in Eq. (3).
Rights and permissions
About this article
Cite this article
Baghshahi, H.R., Haddad, M. & Faghihi, M.J. Geometric discord in a dissipative double-cavity optomechanical system. Quantum Inf Process 20, 239 (2021). https://doi.org/10.1007/s11128-021-03166-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-021-03166-1