Passive-state preparation for continuous variable quantum key distribution in atmospheric channel

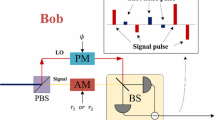
Abstract

The passive-state preparation (PSP) is promising to play an important role in the future on-chip continuous variable quantum key distribution (CVQKD). However, an accurate channel parameter characterization of the PSP-based free-space system has not been established so far. Here, we consider the channel parameter characterization of the PSP-based CVQKD over atmospheric channel. The mode mismatch factor is achieved from combining maximum likelihood with Bayes estimation, leading to a well confidence, whereas the channel transmittance and excess noise can be obtained by using the maximum likelihood estimation. The efficiency of the estimators of the channel parameters is demonstrated by comparing the variances of the estimators with their corresponding quantum Cramér–Rao bounds. We perform numerical simulations of the performance of the PSP-based CVQKD system with experimentally achievable parameters, taking finite-size effect into account based on the characterized channel parameters. Simulation results demonstrate the experiment feasibility of the PSP-based communications over atmospheric channel. Moreover, this parameter characterization method is also suitable for the PSP-based system over other practical channels, such as optical fiber and underwater channels.

Appendices

Appendix

A Excess noise due to the passive-state preparation

To get the estimation of the excess noise caused by the state preparation, we consider characteristics of the X quadrature $x_\mathrm{A}$ of the optical-mode output from Alice’s station. From Fig. 2, it can be written as

$$\begin{aligned} x_\mathrm{A} = \sqrt{\eta \eta _0}x_\mathrm{S} - \sqrt{(1 - \eta )\eta _0}x_{\mathrm{v}_1} - \sqrt{1 - \eta _0}x_{\mathrm{v}_3}, \end{aligned}$$

(15)

where $x_\mathrm{S}$ is the X quadrature of the output mode of the ASE source, $x_{\mathrm{v}_3}$ and $\eta _0$ are the vacuum noise introduced by the variable optical attenuator and the transmittance of it, $x_{\mathrm{v}_1}$ and $\eta$ represent the vacuum noise introduced by the BS and the transmittance of it, respectively. Likewise, $x_\mathrm{a}$ can be expressed as

$$\begin{aligned} x_\mathrm{a}=&\frac{\sqrt{\eta _\mathrm{a}}}{2}(\rho x_\mathrm{S} + \sqrt{1 - \rho ^2}x_\mathrm{S}') + \frac{\sqrt{\eta _\mathrm{a}}}{2}(\rho x_{\mathrm{v}_1} + \sqrt{1 - \rho ^2}x_{\mathrm{v}_1}') \nonumber \\&+ \sqrt{\frac{\eta _\mathrm{a}}{2}}x_{\mathrm{v}_2} - \sqrt{1 - \eta _\mathrm{a}}x_{\mathrm{v}_\mathrm{ax}} + x_\mathrm{el,a}, \end{aligned}$$

(16)

where $x_{\mathrm{v}_2}$ represents the vacuum noise introduced by the BS$_1$, $x_{\mathrm{v}_\mathrm{ax}}$ is the vacuum noise associated with $\eta _\mathrm{a}$, $x_\mathrm{el,a}$ is the noise of Alice’s detector, $x_\mathrm{S}'$ and $x_{\mathrm{v}_1}'$ are the mismatched mode of source and BS (vacuum mode) at Alice’s side, respectively. Given $x_\mathrm{a}$, Alice can make a optimal estimation of the output X-quadrature $x_\mathrm{A}$ by

$$\begin{aligned} x_{\mathrm{A}_e} = \kappa x_\mathrm{a}, \end{aligned}$$

(17)

with

$$\begin{aligned} \kappa = \frac{\langle x_\mathrm{a}x_\mathrm{A}\rangle }{\langle x_\mathrm{a}^2\rangle } = \frac{\sqrt{2\eta (1 - \eta )\eta _0\eta _\mathrm{a}}}{(1 - \eta )\eta _\mathrm{a}n_0+ V_\mathrm{el,a} +1}n_0\rho , \end{aligned}$$

(18)

where $\eta _\mathrm{a}$ is the detection efficiency of Alice’s detector, $n_0$ the average photon number of the thermal source (ASE source), $\rho$ the mode mismatch factor, $V_\mathrm{el,a}$ the electronic noise of Alice’s detector. In the above derivation, we have used the relations of $\langle x_\mathrm{S}^2\rangle = \langle x_\mathrm{S}'^2\rangle = 2n_0 + 1$ [27], $\langle x_\mathrm{el,a}^2\rangle = V_\mathrm{el,a}$, $\langle x_{\mathrm{v}_1}^2\rangle = \langle x_{\mathrm{v}_2}^2\rangle = \langle x_{\mathrm{v}_1}'^2\rangle = \langle x_{\mathrm{v}_\mathrm{ax}}^2\rangle = 1$. Note, all the noise variances are in shot noise units. Alice’s uncertainty on $x_\mathrm{A}$ given her measurement result of $x_\mathrm{a}$ can be given by

$$\begin{aligned} V_{x_\mathrm{A}|x_\mathrm{a}}&= \langle (x_\mathrm{A} - \kappa x_\mathrm{a})^2\rangle \nonumber \\&= \frac{2V_\mathrm{A}\eta \eta _0(V_\mathrm{el,a} +1) + 2\eta (1 - \eta )\eta _\mathrm{a} V_\mathrm{A}^2(1 - \rho ^2)}{(1 - \eta )\eta _\mathrm{a} V_\mathrm{A} + 2\eta \eta _0(V_\mathrm{el,a} +1)} + 1, \end{aligned}$$

(19)

where $V_\mathrm{A} = \eta _0n_0$ is the equivalent modulation variance of Alice. Therefore, the excess noise contributed from the PSP is

$$\begin{aligned} \varepsilon _A = V_{x_\mathrm{A}|x_\mathrm{a}} - 1 = \frac{2V_\mathrm{A}\eta \eta _0(V_\mathrm{el,a} +1) + 2\eta (1 - \eta )\eta _\mathrm{a} V_\mathrm{A}^2(1 - \rho ^2)}{(1 - \eta )\eta _\mathrm{a} V_\mathrm{A} + 2\eta \eta _0(V_\mathrm{el,a} +1)}. \end{aligned}$$

(20)

B Derivation of parameters

To facilitate the calculation below, we rescale $x_\mathrm{a}$ with $\sqrt{\frac{2\eta _0}{\eta _\mathrm{a}}}$ and $x_\mathrm{B}$ with $\sqrt{\frac{2}{\eta _\mathrm{b}}}$, and thus, we have

$$\begin{aligned} x_\mathrm{a}'= \sqrt{\frac{\eta _0}{2}}\rho x_\mathrm{S} + x_\mathrm{aN}', \end{aligned}$$

(21)

$$\begin{aligned} x_\mathrm{B}'= \sqrt{\frac{\eta _0T}{2}}x_\mathrm{S} + x_\mathrm{BN}' \end{aligned}$$

(22)

with

$$\begin{aligned} x_\mathrm{aN}'=&\sqrt{\frac{\eta _0}{2}}\sqrt{1 - \rho ^2} x_\mathrm{S}' + \sqrt{\frac{\eta _0}{2}}(\rho x_{\mathrm{v}_1} + \sqrt{1 - \rho ^2} x_{\mathrm{v}_1}') + \sqrt{\eta _0}x_{\mathrm{v}_2} \nonumber \\&- \sqrt{\frac{2\eta _0(1 - \eta _\mathrm{a})}{\eta _a}}x_{\mathrm{v}_\mathrm{ax}} + \sqrt{\frac{2\eta _0}{\eta _\mathrm{a}}}x_\mathrm{el,a}, \end{aligned}$$

(23)

$$\begin{aligned} x_\mathrm{BN}'=&- \sqrt{\frac{\eta _0T}{2}}x_{\mathrm{v}_1} - \sqrt{(1 - \eta _0)T}x_{\mathrm{v}_3} - \sqrt{1 - T}x_{\mathrm{E}_1} + x_{\mathrm{v}_4} \nonumber \\&- \sqrt{\frac{2(1 - \eta _\mathrm{b})}{\eta _\mathrm{b}}}x_{v_\mathrm{bx}} + \sqrt{\frac{2}{\eta _\mathrm{b}}}x_\mathrm{el,b}, \end{aligned}$$

(24)

where $\eta$ has been set as 0.5, $\eta _\mathrm{b}$ is the detection efficiency of Bob’s detector, T is the transmittance of the channel, $x_{\mathrm{v}_4}$ represents the vacuum noise introduced by the BS$_2$, $x_{\mathrm{E}_1}$ is the excess noise caused by Eve, $x_{\mathrm{v}_\mathrm{bx}}$ is the vacuum noise associated with $\eta _\mathrm{b}$, $x_\mathrm{el,b}$ is the noise of Bob’s detectors. In what follows, we show the calculations of estimators’ mean and variance. The following relations are used for the deviations below: $\langle x_\mathrm{el,b}^2\rangle = V_\mathrm{el,b}$, $V_\mathrm{A} = \eta _0n_0$, $\langle x_{\mathrm{E}_1}^2\rangle = V_{\mathrm{E}_1}$, where $V_{\mathrm{E}_1}$ is the variance of Eve’s EPR state. All the vacuum noise variances are equal to 1.

For estimator ${\widehat{C}}_\mathrm{AB}$, we have

$$\begin{aligned} {\mathbb {E}}({\widehat{C}}_\mathrm{AB})&= \frac{1}{m}\sum _{i = 1}^{m}{\mathbb {E}}(A_i'B_i') = {\mathbb {E}}(x_\mathrm{a}'x_\mathrm{B}') = \frac{\rho \sqrt{T}\eta _0}{2}{\mathbb {E}}(x_\mathrm{S}^2) - \frac{\rho \sqrt{T}\eta _0}{2}{\mathbb {E}}(x_{v1}^2) \nonumber \\&= \rho \sqrt{T}\eta _0n_0 = \rho \sqrt{T}V_\mathrm{A} = C_\mathrm{AB}, \end{aligned}$$

(25)

and

$$\begin{aligned} \mathrm {Var}({\widehat{C}}_\mathrm{AB})&= \frac{1}{m^2}\sum _{i = 1}^{m}\mathrm {Var}(A_i'B_i')= \frac{1}{m}\mathrm {Var}(x_\mathrm{a}'x_\mathrm{B}') \nonumber \\&= \frac{1}{m}\rho ^2TV_\mathrm{A}^2(2 + \frac{1}{n_0})F_1 = {\mathbb {V}}_C, \end{aligned}$$

(26)

where

$$\begin{aligned} F_1=&\frac{1 + \rho ^2}{\rho ^2}\left( 2 + \frac{1}{n_0}\right) + \frac{1}{4\rho ^2TV_\mathrm{A}}F_2 + \frac{1}{\rho ^2T(2n_0 + 1)V_\mathrm{A}}F_3, \end{aligned}$$

(27)

$$\begin{aligned} F_2=&T + 2\left[ V_{\varepsilon } + \frac{2}{\eta _\mathrm{b}} + \frac{2V_\mathrm{el,b}}{\eta _\mathrm{b}}\right] - 3\eta _0T + 2\eta _0T\left( \frac{2}{\eta _\mathrm{a}} + \frac{2V_\mathrm{el,a}}{\eta _\mathrm{a}}\right) , \end{aligned}$$

(28)

$$\begin{aligned} F_3=&\frac{T}{4}(1 + \rho ^2) + \left( \frac{2}{\eta _\mathrm{a}} - 1 + \frac{2V_\mathrm{el,a}}{\eta _\mathrm{a}}\right) \left[ - \eta _0T + V_{\varepsilon } + \frac{2}{\eta _\mathrm{b}} + \frac{2V_\mathrm{el,b}}{\eta _\mathrm{b}}\right] . \end{aligned}$$

(29)

Here, $V_{\varepsilon }=(1 - T)(V_{\mathrm{E}_1} - 1)$ is the untrusted excess noise at Bob’s input.

To demonstrate characteristics of the estimator of the transmittance ${\widehat{T}} = \frac{{\widehat{C}}_\mathrm{AB}^2}{\rho ^2V_\mathrm{A}^2}$, we rearrange the square term

$$\begin{aligned} \left( {\widehat{C}}_\mathrm{AB}\right) ^2 = {\mathbb {V}}_C\left( \frac{{\widehat{C}}_\mathrm{AB}}{\sqrt{{\mathbb {V}}_C}}\right) ^2, \end{aligned}$$

(30)

and then the last expression will be non-centrally $\chi ^2$ distributed

$$\begin{aligned} \left( \frac{{\widehat{C}}_\mathrm{AB}}{\sqrt{{\mathbb {V}}_C}}\right) ^2 \sim \chi ^2\left( 1, \frac{C_\mathrm{AB}^2}{{\mathbb {V}}_C}\right) . \end{aligned}$$

(31)

Therefore, we obtain the mean

$$\begin{aligned} {\mathbb {E}}({\widehat{T}})&= \frac{{\mathbb {V}}_C}{\rho ^2V_\mathrm{A}^2}{\mathbb {E}}\left( \frac{{\widehat{C}}_\mathrm{AB}}{\sqrt{{\mathbb {V}}_C}}\right) ^2 = \frac{{\mathbb {V}}_C}{\rho ^2V_\mathrm{A}^2}\left( 1 + \frac{C_\mathrm{AB}^2}{{\mathbb {V}}_C}\right) \nonumber \\&=T + \frac{1}{m}T(2 + \frac{\eta _0}{V_\mathrm{A}})F_1 = T + O(\frac{1}{m}), \end{aligned}$$

(32)

and the variance

$$\begin{aligned} \mathrm {Var}({\widehat{T}})&= \frac{{\mathbb {V}}_C^2}{\rho ^4V_\mathrm{A}^4}\mathrm {Var}\left( \frac{{\widehat{C}}_\mathrm{AB}}{\sqrt{{\mathbb {V}}_C}}\right) ^2 = \frac{{\mathbb {V}}_C^2}{\rho ^4V_\mathrm{A}^4}2\left( 1 + 2\frac{C_\mathrm{AB}^2}{{\mathbb {V}}_C}\right) \nonumber \\&=\frac{4T^2}{m}(2 + \frac{\eta _0}{V_\mathrm{A}})F_1 + O(\frac{1}{m^2}) = {\mathbb {V}}_T. \end{aligned}$$

(33)

For estimator ${\widehat{V}}_\mathrm{B}$, we have

$$\begin{aligned} {\mathbb {E}}({\widehat{V}}_\mathrm{B})&= \frac{1}{m}\sum _{i = 1}^{m}{\mathbb {E}}((B_i')^2) = {\mathbb {E}}(x_\mathrm{B}'^2) \nonumber \\&= T(V_\mathrm{A} + 1) + 1 + (1 - T)V_{\mathrm{E}_1} + \frac{2(1 - \eta _\mathrm{b} + V_\mathrm{el,b})}{\eta _\mathrm{b}} \nonumber \\&= TV_\mathrm{A} + V_{\varepsilon } + \frac{2(1 + V_\mathrm{el,b})}{\eta _\mathrm{b}} = V_B, \end{aligned}$$

(34)

with the variance given by

$$\begin{aligned} \mathrm {Var}({\widehat{V}}_\mathrm{B}) = \frac{1}{m^2}\sum _{i = 1}^{m}\mathrm {Var}((B_i')^2) = \frac{1}{m}\mathrm {Var}(x_\mathrm{B}'^2) = \frac{2}{m}V_B^2 = {\mathbb {V}}_B. \end{aligned}$$

(35)

To get the variance of estimator ${\hat{\rho }} = {\widehat{C}}_\mathrm{AB}/V_\mathrm{A}\sqrt{{\widehat{T}}'}$, we give an approximate calculation of it. We make a approximation that ${\hat{T}}' \approx {\widehat{V}}_B/V_\mathrm{A}$. Consequently, $\frac{{\widehat{C}}_\mathrm{AB}}{\sqrt{{\mathbb {V}}_C}\sqrt{V_\mathrm{A}{\widehat{T}}'/{\mathbb {V}}_Bm}}$ will be noncentrally t distributed: $\frac{{\widehat{C}}_\mathrm{AB}}{\sqrt{{\mathbb {V}}_C}\sqrt{V_\mathrm{A}{\widehat{T}}'/{\mathbb {V}}_Bm}} \sim t(m,C_\mathrm{AB})$. Then, if we rearrange the estimator ${\widehat{\rho }} = \sqrt{\frac{{\mathbb {V}}_C}{V_\mathrm{A}{\mathbb {V}}_Bm}}\frac{{\widehat{C}}_\mathrm{AB}}{\sqrt{{\mathbb {V}}_C}\sqrt{V_\mathrm{A}{\widehat{T}}'/{\mathbb {V}}_Bm}}$, the variance of the estimator ${\widehat{\rho }}$ can be given by

$$\begin{aligned} \mathrm {Var}({\widehat{\rho }}) \approx \frac{{\mathbb {V}}_C}{V_\mathrm{A}{\mathbb {V}}_Bm}\left( \frac{m(1 + C_\mathrm{AB}^2)}{m - 2} - \frac{mC_\mathrm{AB}^2}{2}\left[ \Gamma (\frac{m-1}{2})/\Gamma (\frac{m}{2})\right] ^2\right) , \end{aligned}$$

(36)

where $\Gamma (\cdot )$ is the Gamma function.

We find that $B_i' - \tau A_i'$ is normally distributed with variance $V_\mathrm{N}$, and thus, $Y := \sum _{i = 1}^{m}(\frac{B_i' - \tau A_i'}{\sqrt{V_\mathrm{N}}})^2$ is a $\chi ^2$ distribution with mean value of m and variance of 2m. Then, the mean value of ${\widehat{V}}_\mathrm{N}$ is calculated as

$$\begin{aligned} {\mathbb {E}}({\widehat{V}}_\mathrm{N}) = {\mathbb {E}}\left( \frac{1}{m}\sum _{i = 1}^{m}(B_i' - {\widehat{\tau }}A_i')^2\right) = \frac{1}{m}V_\mathrm{N}{\mathbb {E}}(Y) = V_\mathrm{N}. \end{aligned}$$

(37)

On the other hand, we have

$$\begin{aligned} {\mathbb {E}}({\widehat{V}}_\mathrm{N}) =&\frac{1}{m}\sum _{i = 1}^{m}{\mathbb {E}}((B_i' - {\widehat{\tau }}A_i')^2) = {\mathbb {E}}((x_\mathrm{B}' - \tau x_\mathrm{a}')^2) \nonumber \\ =&V_{\varepsilon } + \frac{2 + 2V_\mathrm{el,b}}{\eta _\mathrm{b}} + \frac{\eta _0T}{2}[(2n_0 + 1)(1 - \rho ^2) - 1 + 3\rho ^2 \nonumber \\&+ \frac{2\rho ^2}{\eta _\mathrm{a}}(2 + 2V_\mathrm{el,a} - \eta _\mathrm{a})] = V_\mathrm{N}. \end{aligned}$$

(38)

The variance of ${\widehat{V}}_\mathrm{N}$ is given by

$$\begin{aligned} \mathrm {Var}({\widehat{V}}_\mathrm{N}) = \mathrm {Var}\left( \frac{1}{m}\sum _{i = 1}^{m}(B_i' - {\widehat{\tau }}A_i')^2\right) = \frac{1}{m^2}V_\mathrm{N}^2\mathrm {Var}(Y) = \frac{2}{m}V_\mathrm{N}^2 = {\mathbb {V}}_{N}. \end{aligned}$$

(39)

Therefore, the mean of the estimated excess noise ${\widehat{V}}_{\varepsilon }$ is calculated as

$$\begin{aligned} {\mathbb {E}}({\widehat{V}}_{\varepsilon }) =&V_\mathrm{N} - \frac{2 + 2V_\mathrm{el,b}}{\eta _\mathrm{b}} - \frac{\eta _0T}{2}[(2n_0 + 1)(1 - \rho ^2)- 1 \nonumber \\&+ 3\rho ^2 + \frac{2\rho ^2}{\eta _\mathrm{a}}(2 + 2V_\mathrm{el,a}- \eta _\mathrm{a})] = V_{\varepsilon }. \end{aligned}$$

(40)

The variance of ${\widehat{V}}_{\varepsilon }$ is derived as

$$\begin{aligned} \mathrm {Var}({\widehat{V}}_{\varepsilon })=&\mathrm {Var}({\widehat{V}}_\mathrm{N}) + \frac{\eta _0^2\mathrm {Var}({\widehat{T}})}{4}[(2n_0 + 1)(1 - \rho ^2) - 1 + 3\rho ^2 \nonumber \\&- \frac{2\rho ^2}{\eta _\mathrm{a}}(2 + 2V_\mathrm{el,a} - \eta _\mathrm{a})]^2 = {\mathbb {V}}_{\varepsilon }, \end{aligned}$$

(41)

which is of order 1/m.

C Derivations of QFIM and QCBR

In quantum estimation theory, the optimal precision in estimating parameters is given by the quantum Cramér–Rao bounds (QCRB), which can be obtained from the inverse of the quantum Fisher information matrix (QFIM) of the corresponding parameters. There are two QCRBs most used. One is based on the right logarithmic derivative (RLD) QFIM, and the other is based on the symmetric logarithmic derivative (SLD) QFIM. Consider a quantum system described by a density operator ${\hat{\varrho }}(\theta _d)$, where $\theta _d = \{\theta _1,\ldots ,\theta _M\}$ is the set of parameters contained in the quantum system. The RLD and SLD operators for each of the parameters involved are, respectively, obtained from the following differential equations [34]

$$\begin{aligned} \frac{\partial {\hat{\varrho }}}{\partial \theta _d}= & {} {\hat{\varrho }}\hat{\mathcal {L}}_{\theta _d}^{R}, \end{aligned}$$

(42)

$$\begin{aligned} \frac{\partial {\hat{\varrho }}}{\partial \theta _d}= & {} \frac{1}{2}\left\{ {\hat{\varrho }},{\hat{L}}_{\theta _d}^{S}\right\} , \end{aligned}$$

(43)

where $\hat{\mathcal {L}}_{\theta _d}^{R}$ and ${\hat{L}}_{\theta _d}^{S}$ are the RLD and SLD operators, respectively, and $\{.,.\}$ represents anticommutation. The quantum Fisher information matrices associated with RLD and SLD are, respectively, given by

$$\begin{aligned} \mathcal {F}_{\theta _d\theta _l}= & {} \mathrm {Tr}\left[ {\hat{\varrho }}\hat{\mathcal {L}}_{\theta _d}^{R}\hat{\mathcal {L}}_{\theta _l}^{R\dag }\right] , \end{aligned}$$

(44)

$$\begin{aligned} \mathcal {H}_{\theta _d\theta _l}= & {} \frac{1}{2} \mathrm {Tr}\left[ {\hat{\varrho }}\left\{ {\hat{L}}_{\theta _d}^{S},{\hat{L}}_{\theta _l}^{S}\right\} \right] . \end{aligned}$$

(45)

The corresponding QCBRs are expressed by [34]

$$\begin{aligned} \mathbf {Cov}[{\hat{\theta }}]\geqslant & {} \frac{\mathrm {Re}\left[ \mathcal {F}^{-1}\right] + |\mathrm {Im}\left[ \mathcal {F}^{-1}\right] |}{m}, \end{aligned}$$

(46)

$$\begin{aligned} \mathbf {Cov}[{\hat{\theta }}]\geqslant & {} \frac{\mathcal {H}^{-1}}{m}, \end{aligned}$$

(47)

where $\mathbf {Cov}[{\hat{\theta }}]$ denotes the covariance matrix of the set of parameters $\theta _d = \{\theta _1,\ldots ,\theta _M\}$, and $|\bullet |$ is the absolute value of the quantity $\bullet$. Applying trace operator to Eq. (46) and (47), we find that the sum of the variances of the estimated parameters is given by [34]

$$\begin{aligned} \sum _{d}^{M}\mathrm {Var}(\theta _d)\geqslant B_R= & {} \frac{\mathrm {Tr}\left[ \mathrm {Re}\left[ \mathcal {F}^{-1}\right] \right] +\mathrm {Tr}\left[ |\mathrm {Im}\left[ \mathcal {F}^{-1}\right] |\right] }{m}, \end{aligned}$$

(48)

$$\begin{aligned} \sum _{d}^{M}\mathrm {Var}(\theta _d)\geqslant B_S= & {} \frac{\mathrm {Tr}\left[ \mathcal {H}^{-1}\right] }{m}, \end{aligned}$$

(49)

where $B_R$ and $B_S$ are the corresponding QCBRs associated with RLD and SLD, respectively. It has been demonstrated that the QFIM of a Gaussian state can be described only by the first and second moments [34]. The RLD QFIM of a Gaussian state is given by

$$\begin{aligned} \mathcal {F}_{\theta _d\theta _l} = \frac{1}{2}\mathrm {vec}\left[ \frac{\partial {\Gamma }}{\partial \theta _d}\right] ^{\dag } {\Xi }^{+} \mathrm {vec}\left[ \frac{\partial {\Gamma }}{\partial \theta _l}\right] +2\frac{\partial {\mathbf {d}}^{\mathrm {T}}}{\partial \theta _d}{\Sigma }^{+} \frac{\partial {\mathbf {d}}}{\partial \theta _l} \end{aligned}$$

(50)

with ${\Sigma } = {\Gamma } + i{\Omega }$, where ${\Omega } = \oplus _{i=1}^{N}\omega , \omega = \left( \begin{array}{ll} 0 &{}\quad 1 \\ -1 &{}\quad 0 \\ \end{array} \right)$, where ${\Gamma }$ is the covariance matrix of the N mode Gaussian state, ${\mathbf {d}}$ is the first moment called the displacement vector, $\mathrm {vec}[A]$ is the vectorization of a matrix A which defined for any $t\times t$ real or complex matrix A as: $\mathrm {vec}[A] = (a_{11},\ldots ,a_{t1},\ldots ,a_{t1},\ldots ,a_{tt})^{\mathrm {T}}$, ${\Xi }^{+} = ({\Sigma }^{\dag }\otimes {\Sigma })^{+}$ and ‘+’ denotes the Moore–Penrose pseudoinverse. The SLD QFIM of a Gaussian state can be given as

$$\begin{aligned} \mathcal {H}_{\theta _d\theta _l} = \frac{1}{2}\mathrm {vec}\left[ \frac{\partial {\Gamma }}{\partial \theta _d}\right] ^{\dag } \mathcal {M}^{+} \mathrm {vec}\left[ \frac{\partial {\Gamma }}{\partial \theta _l}\right] + 2\frac{\partial {\mathbf {d}}^{\mathrm {T}}}{\partial \theta _d}{\Gamma }^{-1}\frac{\partial {\mathbf {d}}}{\partial \theta _l}, \end{aligned}$$

(51)

where $\mathcal {M} = ({\Gamma }^{\dag }\otimes {\Gamma } + {\Omega }\otimes {\Omega })$. The QCRB associated with SLD can be saturated if and only if [34]

$$\begin{aligned} \mathrm {Im}\left( \mathrm {Tr}\left[ {\hat{\varrho }}{\hat{L}}_{\theta _d}^{S}{\hat{L}}_{\theta _l}^{S} \right] \right) =&2\mathrm {vec}\left[ \frac{\partial {\Gamma }}{\partial \theta _d}\right] ^{\dag } \mathcal {M}^{+}({\Gamma }\otimes {\Omega })\mathcal {M}^{+} \mathrm {vec}\left[ \frac{\partial {\Gamma }}{\partial \theta _l}\right] \nonumber \\&+ 2\frac{\partial {\mathbf {d}}^{\mathrm {T}}}{\partial \theta _d}{\Gamma }^{-1}{\Omega }{\Gamma }^{-1} \frac{\partial {\mathbf {d}}}{\partial \theta _l} = 0. \end{aligned}$$

(52)

Since the proposed PSP-based CVQKD scheme involves thermal state and Gaussian operations, the QFIM can be determined through the covariance matrix of the bilateral state of Alice and Bob before they perform heterodyne detection. The covariance matrix of the bilateral state $\varrho _\mathrm{AB}$ between Alice and Bob before they perform heterodyne detection can be given by

$$\begin{aligned} {\Gamma }_\mathrm{AB} = \left( \begin{array}{ll} \langle x_1^2\rangle {\mathbf {I}} &{}\quad \langle x_1x_2\rangle {\mathbf {I}} \\ \langle x_1x_2\rangle {\mathbf {I}} &{}\quad \langle x_2^2\rangle {\mathbf {I}} \\ \end{array} \right) \end{aligned}$$

(53)

with

$$\begin{aligned} x_1= & {} \sqrt{\frac{1}{2}}(\rho x_\mathrm{S} + \sqrt{1 - \rho ^2}x_\mathrm{S}') + \sqrt{\frac{1}{2}}(\rho x_{\mathrm{v}_1} + \sqrt{1 - \rho ^2}x_{\mathrm{v}_1}'), \end{aligned}$$

(54)

$$\begin{aligned} x_2= & {} \sqrt{\frac{\eta _0T}{2}}x_\mathrm{S} - \sqrt{\frac{\eta _0T}{2}}x_{\mathrm{v}_1} - \sqrt{(1 - \eta _0)T}x_{\mathrm{v}_3} - \sqrt{1 - T}x_{\mathrm{E}_1}, \end{aligned}$$

(55)

where ${\mathbf {I}} = \left( \begin{array}{ll} 1 &{}\quad 0 \\ 0 &{}\quad 1 \\ \end{array} \right)$, $\langle x_1^2\rangle = n_0 + 1$, $\langle x_2^2\rangle = TV_\mathrm{A} + V_{\varepsilon } + 1$, and $\langle x_1x_2\rangle = \sqrt{\eta _0T}\rho n_0$. The displacement vector of the bilateral state $\varrho _\mathrm{AB}$ is ${\mathbf {d}}_\mathrm{AB} = {\mathbf {0}}$. Following the above analysis, we can easily obtain the QFIM and the corresponding QCRBs of parameters T and $\rho$ while checking the efficiency of estimators ${\widehat{T}}'$ and ${\widehat{\rho }}$. Similarly, the QFIM and the corresponding QCRBs of parameters T and $V_{\varepsilon }$ can be acquired while discussing the efficiency of estimators ${\widehat{T}}$ and ${\widehat{\rho }}$. We also find that Eq. (52) is always satisfied for parameters T and $\rho$ or parameters T and $V_{\varepsilon }$, which means the SLD-based QCRB is attainable for simultaneously estimating parameters T and $\rho$ or parameters T and $V_{\varepsilon }$.

D Elliptic-beam model

Free-space channel has a fluctuated transmissivity with a certain probability distribution, which can be described by the elliptic-beam model [29]. This model has a well matching of atmospheric effects in terms of beam wandering, beam broadening and beam shape deformation, rendering the Gaussian beam profile into an elliptical form. The received elliptic beam is modeled by a random vector $\varpi = (x_0,y_0,\Theta _1,\Theta _2,\phi )$, where $(x_0,y_0)$ is the beam-centroid coordinate in the received aperture plane, $\Theta _i (i = 1,2)$ is related to the semi-axes $W_i$ of the elliptic spot, as $W_i^2 = W_0^2\mathrm {exp}(\Theta _i)$ with $W_0$ the initial beam-spot radius. Parameters $(x_0,y_0,\Theta _1,\Theta _2)$ are assumed to be a four-dimensional Gaussian distribution, while parameter $\phi$ is assumed to be a uniform distribution in $[0,\pi /2]$ and has no correlation with other parameters. Assuming that $\langle x_0\rangle = \langle y_0\rangle = 0$, correlations between $x_0,y_0$ and $\Theta _i$ vanish. Based on the above assumption, vector $\varpi ' = (x_0,y_0,\Theta _1,\Theta _2)$ can be characterized by the following covariance matrix [29]

$$\begin{aligned} \Sigma= & {} \left( \begin{array}{llll} \langle \Delta x_0^2\rangle &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \langle \Delta y_0^2\rangle &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad \langle \Delta \Theta _1^2\rangle &{}\quad \langle \Delta \Theta _1\Delta \Theta _2\rangle \\ 0 &{}\quad 0 &{}\quad \langle \Delta \Theta _1\Delta \Theta _2\rangle &{}\quad \langle \Delta \Theta _2^2\rangle \\ \end{array} \right) \end{aligned}$$

(56)

with the mean value $(0,0,\langle \Delta \Theta _1\rangle ,\langle \Delta \Theta _2\rangle )$. The mean values and the elements of the covariance matrix for weak and weak-to-moderate turbulence are given as [29]

$$\begin{aligned} \langle \Delta \Theta _1\rangle = \langle \Delta \Theta _2\rangle&= \mathrm {ln}\left[ \frac{(1 + 2.96\sigma _R^2\Omega ^{5/6})^2}{\Omega ^2\sqrt{(1+ 2.96\sigma _R^2\Omega ^{5/6})^2 + 1.2\sigma _R^2\Omega ^{5/6}}}\right] , \end{aligned}$$

(57)

$$\begin{aligned} \langle \Delta x_0^2\rangle = \langle \Delta y_0^2\rangle&= 0.33W_0^2\sigma _R^2\Omega ^{-7/6}, \end{aligned}$$

(58)

$$\begin{aligned} \langle \Delta \Theta _1^2\rangle = \langle \Delta \Theta _2^2\rangle&= \mathrm {ln}\left[ 1 + \frac{1.2\sigma _R^2\Omega ^{5/6}}{(1+ 2.96\sigma _R^2\Omega ^{5/6})^2}\right] , \end{aligned}$$

(59)

$$\begin{aligned} \langle \Delta \Theta _1\Delta \Theta _2\rangle&= \mathrm {ln}\left[ 1 - \frac{0.8\sigma _R^2\Omega ^{5/6}}{(1+ 2.96\sigma _R^2\Omega ^{5/6})^2}\right] . \end{aligned}$$

(60)

where $\Omega = \pi W_0^2/\lambda L$, $\sigma _R^2$ is the Rytov variance. For strong turbulence, they are given by [29]

$$\begin{aligned} \langle \Delta \Theta _1\rangle&= \langle \Delta \Theta _2\rangle \nonumber \\&= \mathrm {ln}\left[ \frac{(\gamma + 1.17\sigma _R^{12/5}\Omega ^{-1} - 2.99\sigma _R^{8/5}\Omega ^{-1})^2}{\sqrt{(\gamma + 1.71\sigma _R^{12/5}\Omega ^{-1} - 2.99\sigma _R^{8/5}\Omega ^{-1})^2 + 3.24\gamma \sigma _R^{12/5}\Omega ^{-1}}}\right] ,\nonumber \\ \end{aligned}$$

(61)

$$\begin{aligned} \langle \Delta x_0^2\rangle&= \langle \Delta y_0^2\rangle = 0.75W_0^2\sigma _R^{8/5}\Omega ^{-1}, \end{aligned}$$

(62)

$$\begin{aligned} \langle \Delta \Theta _1^2\rangle&= \langle \Delta \Theta _2^2\rangle = \mathrm {ln}\left[ 1 + \frac{12.14\gamma \sigma _R^{12/5}\Omega ^{-1}}{(\gamma + 1.71\sigma _R^{12/5}\Omega ^{-1} - 2.99\sigma _R^{8/5}\Omega ^{-1})^2}\right] , \end{aligned}$$

(63)

$$\begin{aligned} \langle \Delta \Theta _1\Delta \Theta _2\rangle&= \mathrm {ln}\left[ 1 + \frac{0.65\gamma \sigma _R^{12/5}\Omega ^{-1}}{(\gamma + 1.71\sigma _R^{12/5}\Omega ^{-1} - 2.99\sigma _R^{8/5}\Omega ^{-1})^2}\right] , \end{aligned}$$

(64)

where $\gamma = (1 + \Omega ^2)/\Omega ^2$. The Rytov variance $\sigma _R^2$ is defined as $\sigma _R^2 = 1.23C_n^2k_n^{7/6}L^{11/6}$, where $k_n$ is the optical wave number, L the transmission distance, $C_n^2$ the atmospheric index-of-refraction structure constant. Note, turbulence intensities for weak, moderate and strong turbulence are corresponding to $\sigma _R^2 < 1, \sigma _R^2 \approx 1\sim 10$ and $\sigma _R^2 > 10$, respectively.

With the above parameters, the probability distribution of the transmission $T_{tur}$ caused by turbulence can then be evaluated using Monte Carlo method by [29]

$$\begin{aligned} {{T_{tur}}}={{T}_{0}}\exp \left\{ -{{\left[ \frac{r/a}{R\left( \frac{2}{{{W}_\mathrm{eff}}\left( \phi \right) } \right) } \right] }^{\lambda \left( \frac{2}{{{W}_\mathrm{eff}}\left( \phi \right) } \right) }} \right\} , \end{aligned}$$

(65)

where

$$\begin{aligned} \lambda \left( \xi \right)= & {} 2a^{2}{{\xi }^{2}}\frac{\exp \left( -a^{2}{{\xi }^{2}} \right) {{I}_{1}}\left( a^{2}{{\xi }^{2}} \right) }{1-\exp \left( -a^{2}{{\xi }^{2}} \right) {{I}_{0}}\left( a^{2}{{\xi }^{2}} \right) } \nonumber \\&\times \left[ \ln \left( 2\frac{1-\exp \left( -\frac{1}{2}a^{2}{{\xi }^{2}} \right) }{1-\exp \left( -a^{2}{{\xi }^{2}} \right) {{I}_{0}}\left( a^{2}{{\xi }^{2}} \right) } \right) \right] , \end{aligned}$$

(66)

$$\begin{aligned} R\left( \xi \right)= & {} \left[ \mathrm {ln}\left( 2\frac{1-\exp \left( -\frac{1}{2}a^{2}{\xi }^{2} \right) }{1-\exp \left( -a^{2}\xi ^{2} \right) {I}_{0}\left( a^{2}\xi ^{2} \right) } \right) \right] ^{-\frac{1}{\lambda \left( \xi \right) }}, \end{aligned}$$

(67)

$$\begin{aligned} {{T}_{0}}= & {} 1-{{I}_{0}}\left( a^{2}\frac{W_{1}^{2}-W_{2}^{2}}{W_{1}^{2}W_{2}^{2}} \right) \exp \left[ -a^{2}\frac{W_{1}^{2}+W_{2}^{2}}{W_{1}^{2}W_{2}^{2}} \right] - \nonumber \\&2\left\{ 1-\exp \left[ -\frac{a^{2}}{2}{{\left( \frac{1}{{{W}_{1}}}-\frac{1}{{{W}_{2}}} \right) }^{2}} \right] \right\} \nonumber \\&\times \exp \left\{ -\left[ \frac{\frac{\left( {{W}_{1}}+{{W}_{2}} \right) ^{2}}{\left| W_{1}^{2}-W_{2}^{2} \right| }}{R\left( \frac{1}{{W}_{1}}-\frac{1}{{W}_{2}} \right) }\right] ^{\lambda \left( \frac{1}{{W}_{1}}-\frac{1}{{W}_{2}} \right) } \right\} , \end{aligned}$$

(68)

$$\begin{aligned} W_\mathrm{eff}^{2}\left( \phi \right)= & {} 4a^{2} \left[ \omega \left( \frac{4a^{2}}{{{W}_{1}}{{W}_{2}}}e^{ \frac{a^{2}}{W_{1}^{2}}\left( 1+2{{\cos }^{2}}\phi \right) + \frac{a^{2}}{W_{2}^{2}}\left( 1+2{{\sin }^{2}}\phi \right) } \right) \right] ^{-1}, \end{aligned}$$

(69)

$r = x_0^2 + y_0^2$, a is the receiving lens radius. Here, $\omega (\cdot )$ denotes the Lambert W function.

E Calculations of the secret key rate

As the PSP-based CVQKD protocol is equivalent to the GMCS-based CVQKD protocol, the security analysis here refers to the GMCS scheme. We consider the equivalent entanglement-based scheme of the PSP-based CVQKD protocol. The covariance matrix of the ensemble-average state $\rho _\mathrm{AB}$ at the output of the fluctuating channel is given by [31]

$$\begin{aligned} \Gamma _\mathrm{AB}= & {} \left( \begin{array}{ll} V{\mathbf {I}} &{} \quad \sqrt{T_e}\sqrt{V^2 - 1}\sigma _Z\\ \sqrt{T_e}\sqrt{V^2 - 1}\sigma _Z &{} \quad T_e(V + \chi _\mathrm{line}){\mathbf {I}} \end{array} \right) , \end{aligned}$$

(70)

with the parameters

$$\begin{aligned}&V = V_\mathrm{A} + 1, \end{aligned}$$

(71)

$$\begin{aligned}&T_e = \langle \sqrt{T}\rangle ^2, \end{aligned}$$

(72)

$$\begin{aligned}&\chi _\mathrm{line} = \frac{1 - T_e}{T_e} + \varepsilon _e + \varepsilon _A, \end{aligned}$$

(73)

$$\begin{aligned}&\varepsilon _e = \frac{\mathrm {Var}(\sqrt{T})(V - 1) + \langle V_{\varepsilon }\rangle }{T_e}, \end{aligned}$$

(74)

$$\begin{aligned}&\mathrm {Var}(\sqrt{T}) = \langle T\rangle - \langle \sqrt{T}\rangle ^2, \end{aligned}$$

(75)

where ${\mathbf {I}} = \bigg (\begin{array}{ll} 1 &{}\quad 0 \\ 0 &{}\quad 1 \end{array}\bigg )$, $\sigma _Z = \bigg (\begin{array}{ll} 1 &{}\quad 0 \\ 0 &{}\quad -1 \end{array}\bigg )$, $T_e$ and $\chi _\mathrm{line}$ are the effective transmittance and channel added excess noise, respectively. We assume that $\langle V_{\varepsilon }\rangle = \langle T\rangle \varepsilon _0$ for simplicity, where $\varepsilon _0$ represents the untrusted excess noise. In practical implementation, $\langle V_{\varepsilon }\rangle$ should be regarded as $\langle T\varepsilon _0(T)\rangle$, where $\varepsilon _0(T)$ should be a function related to T. Note, for a conservative estimation, we also assume that $\varepsilon _A$ is controlled by Eve, and hence its magnitude, or the value of $\rho$, will greatly impact the performance of the system.

For the case of reverse reconciliation, the asymptotical secret key rate of the GMCS CVQKD is given as [27]

$$\begin{aligned} K_{asy} = \beta I_\mathrm{AB} - \chi _{BE}, \end{aligned}$$

(76)

where $I_\mathrm{AB}$ is the Shannon mutual information between Alice and Bob, $\beta$ is the reconciliation efficiency, $\chi _\mathrm{BE}$ is the Holevo bound on Eve’s information about Bob’s secret key. Considering the practical imperfection of the detector at Bob’s side, the mutual information between Alice and Bob is given by [27]

$$\begin{aligned} I_\mathrm{AB} = \log \left( \frac{V + \chi _\mathrm{tot}}{1 + \chi _\mathrm{tot}}\right) , \end{aligned}$$

(77)

where

$$\begin{aligned} \chi _\mathrm{tot}= & {} \chi _\mathrm{line} + \frac{\chi _\mathrm{det}}{T_e}, \end{aligned}$$

(78)

$$\begin{aligned} \chi _\mathrm{det}= & {} \frac{1 + (1 - \eta _\mathrm{b}) + 2V_\mathrm{el,b}}{\eta _\mathrm{b}}. \end{aligned}$$

(79)

Under the noise model that Eve cannot control the imperfection of Bob’s system, the Holevo bound between Eve and Bob can be given by

$$\begin{aligned} \chi _{BE} = \sum _{j = 1}^{2}G\left( \frac{\lambda _j - 1}{2}\right) - \sum _{j = 3}^{5}G\left( \frac{\lambda _j - 1}{2}\right) , \end{aligned}$$

(80)

where $G(x) = (x + 1)\log _2(x + 1) - x\log _2x$. The symplectic eigenvalues $\lambda _{1,2}$ take the form as

$$\begin{aligned} \lambda _{1,2}^2 = \frac{1}{2}[{\mathbb {A}} \pm \sqrt{{\mathbb {A}}^2 - 4{\mathbb {B}}}], \end{aligned}$$

(81)

with

$$\begin{aligned} {\mathbb {A}}= & {} V^2 + T_e^2(V + \chi _\mathrm{line})^2 - 2T_e(V^2 - 1), \end{aligned}$$

(82)

$$\begin{aligned} {\mathbb {B}}= & {} \left( VT_e(V + \chi _\mathrm{line}) - T_e^2(V^2 - 1)\right) ^2. \end{aligned}$$

(83)

The symplectic eigenvalues $\lambda _{3,4}$ have the same form as

$$\begin{aligned} \lambda _{3,4}^2 = \frac{1}{2}[{\mathbb {C}} \pm \sqrt{{\mathbb {C}}^2 - 4{\mathbb {D}}}], \end{aligned}$$

(84)

where

$$\begin{aligned} {\mathbb {C}} =&\frac{1}{(T_e(V + \chi _\mathrm{tot}))^2}[{\mathbb {A}}\chi _\mathrm{det}^2 + {\mathbb {B}} + 2T_e(V^2 - 1) + 1 \nonumber \\&+ 2\chi _\mathrm{det}(V\sqrt{{\mathbb {B}}} + T_e(V + \chi _\mathrm{line}))], \end{aligned}$$

(85)

$$\begin{aligned} {\mathbb {D}} =&\left( \frac{V + \sqrt{{\mathbb {B}}}\chi _\mathrm{det}}{T_e(V + \chi _\mathrm{tot})}\right) ^2. \end{aligned}$$

(86)

The symplectic eigenvalue $\lambda _5 = 1$.

Considering finite-size effect, the secret key rate is given by [31, 32]

$$\begin{aligned} K_\mathrm{finite} = \frac{n}{N}[K_\mathrm{asy}(\langle \sqrt{T}\rangle ^\mathrm{low}, \langle T\rangle ^\mathrm{up}, \langle V_{\varepsilon }\rangle ^\mathrm{up}) - \Delta (n) ], \end{aligned}$$

(87)

where N is the total exchanged data, $n = N - M$ is the data used for generating row key, M is the total data used for parameter estimation in each round, $\langle \sqrt{T}\rangle ^{low} = \langle \sqrt{T}\rangle - 6.5\sqrt{\langle \mathrm {Var}( \sqrt{{\widehat{T}}})\rangle }$, $\langle T\rangle ^{up} = \langle T\rangle + 6.5\sqrt{\langle {\mathbb {V}}_T\rangle }$, $\langle V_{\varepsilon }\rangle ^{up} = \langle V_{\varepsilon }\rangle + 6.5\sqrt{\langle {\mathbb {V}}_{\varepsilon }\rangle }$ [32], $\Delta (n)$ is given as [6]

$$\begin{aligned} \Delta (n) = 7\sqrt{\frac{\mathrm {log_2}(2/\epsilon _\mathrm{sm})}{n}} + \frac{2}{n}\mathrm {log_2}(1/\epsilon _\mathrm{PA}), \end{aligned}$$

(88)

where $\epsilon _\mathrm{sm}$ is a smoothing parameter, $\epsilon _\mathrm{PA}$ is the failure probability of the privacy amplification procedure. Here, we use $\langle T\rangle$ and $\langle T^2\rangle$ replace T and $T^2$ in ${\mathbb {V}}_T$ and ${\mathbb {V}}_{\varepsilon }$ to obtain the ensemble-average variance of $\langle {\mathbb {V}}_T\rangle$ and $\langle {\mathbb {V}}_{\varepsilon }\rangle$. The variance of $\mathrm {Var}\left( \sqrt{{\widehat{T}}}\right)$ can be calculated as

$$\begin{aligned} \mathrm {Var}\left( \sqrt{{\widehat{T}}}\right)&=\mathrm {Var}\left( \frac{{\widehat{C}}_\mathrm{AB}}{\rho V_\mathrm{A}}\right) = \frac{{\mathbb {V}}_C}{\rho ^2V_\mathrm{A}^2}\mathrm {Var}\left( \frac{{\widehat{C}}_\mathrm{AB}}{\sqrt{{\mathbb {V}}_C}}\right) \nonumber \\&=\frac{{\mathbb {V}}_C}{\rho ^2V_\mathrm{A}^2} = \frac{1}{m}T\left( 2 + \frac{\eta _0}{V_\mathrm{A}}\right) F_1 = {\mathbb {V}}_{\sqrt{T}}. \end{aligned}$$

(89)

Likewise, we use $\langle T\rangle$ and $\langle T^2\rangle$ replace T and $T^2$ in ${\mathbb {V}}_{\sqrt{T}}$ to obtain the ensemble-average variance of $\langle {\mathbb {V}}_{\sqrt{T}}\rangle$. We assume that $\epsilon _\mathrm{sm} = \epsilon _\mathrm{PA} = 10^{-10}$ in this paper.