Skip to main content
Springer Nature Link
Log in

Quantum multi-image compression-encryption scheme based on quantum discrete cosine transform and 4D hyper-chaotic Henon map

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

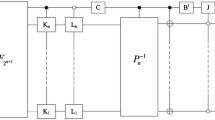
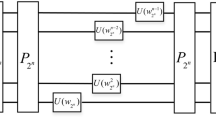
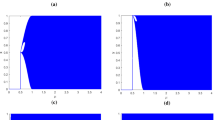
A new quantum multi-image compression and encryption algorithm combining quantum discrete cosine transform with 4D hyper-chaotic Henon map is proposed. The four original images are firstly transformed by quantum discrete cosine transform, and then the obtained frequency coefficient matrices are compressed with the measurement matrices to construct four compressed images. Subsequently, four compressed images are selected to reconstruct a new quantum image. Under the control of four initial values and two parameters, a quantum key image is constructed by a 1D chaotic sequence originated from the 4D hyper-chaotic Henon map, and XORed with the reconstructed quantum image. Ultimately, to enhance the security of the algorithm, the cycle shift operations controlled by the logistic map are employed to scramble the pixels of the produced quantum image to acquire the encryption image. Numerical simulations confirm the reliability and the security of the designed quantum multi-image compression and encryption algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig.6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Deepak, V.K., Rajakumaran, C., Kavitha, R.: Chaos based encryption of quantum images. Multimed. Tools Appl. 79(5), 23849–23860 (2020)

    Article  Google Scholar 

  2. Yan, F., Iliyasu, A.M., Venegas-Andraca, S.E.: A survey of quantum image representations. Quantum Inf. Process. 15(1), 1–35 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  3. Li, H.S., Zhu, Q., Zhou, R.G., Song, L., Yang, X.J.: Multi-dimensional color image storage and retrieval for a normal arbitrary quantum superposition state. Quantum Inf. Process. 13(4), 991–1011 (2014)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  4. Venegas-Andraca, S.E., Bose, S.: Storing, processing, and retrieving an image using quantum mechanics. Proc. SPIE Int. Soc. Opt. Eng. 5105, 1085–1090 (2003)

    Google Scholar 

  5. Le, P.Q., Dong, F., Hirota, K.: A flexible representation of quantum images for polynomial preparation, image compression, and processing operations. Quantum Inf. Process. 10(1), 63–84 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  6. Zhang, Y., Lu, K., Gao, Y.H., Wang, M.: NEQR: A novel enhanced quantum representation of digital images. Quantum Inf. Process. 12(8), 2833–2860 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  7. Jiang, N., Wang, J., Mu, Y.: Quantum image scaling up based on nearest-neighbor interpolation with integer scaling ratio. Quantum Inf. Process. 14(11), 4001–4026 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  8. Song, X.H., Wang, S., El-Latif, A., Niu, X.M.: Quantum image encryption based on restricted geometric and color transformations. Quantum Inf. Process. 13(8), 1765–1787 (2014)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  9. Abd-El-Atty, B., El-Latif, A., Venegas-Andraca, S.E.: An encryption protocol for NEQR images based on one-particle quantum walks on a circle. Quantum Inf. Process. 18(9), 272 (2019)

    Article  ADS  Google Scholar 

  10. Liu, X.B., Xiao, D., Liu, C.: Quantum image encryption algorithm based on bit-plane permutation and sine logistic map. Quantum Inf. Process. 19(8), 1570–1573 (2020)

    Article  MathSciNet  Google Scholar 

  11. Khan, M., Rasheed, A.: Permutation-based special linear transforms with application in quantum image encryption algorithm. Quantum Inf. Process. 18(10), 298 (2019)

    Article  ADS  Google Scholar 

  12. Jiang, N., Dong, X., Hu, H., Ji, Z.X., Zhang, W.Y.: Quantum image encryption based on Henon mapping. Int. J. Theor. Phys. 58(3), 979–991 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  13. Tan, R.C., Lei, T., Zhao, Q.M., Gong, L.H., Zhou, Z.H.: Quantum color image encryption algorithm based on a hyper-chaotic system and quantum Fourier transform. Int. J. Theor. Phys. 55(12), 5368–5384 (2016)

    Article  MATH  Google Scholar 

  14. Yang, Y.G., Xia, J., Jia, X., Zhang, H.: Novel image encryption/decryption based on quantum Fourier transform and double phase encoding. Quantum Inf. Process. 12(11), 3477–3493 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  15. Li, H.S., Li, C.Y., Chen, X., Xia, H.Y.: Quantum image encryption based on phase-shift transform and quantum Haar wavelet packet transform. Mod. Phys. Lett. A 34(26), 1950214 (2019)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  16. Hu, W.W., Zhou, R.G., Luo, J., Jiang, S.X., Luo, G.F.: Quantum image encryption algorithm based on Arnold scrambling and wavelet transforms. Quantum Inf. Process. 19(3), 82 (2020)

    Article  ADS  MathSciNet  Google Scholar 

  17. Ko, H.J., Huang, C.T., Horng, G., Wang, S.J.: Robust and blind image watermarking in DCT domain using inter-block coefficient correlation. Inform. Sciences 517, 128–147 (2020)

    Article  Google Scholar 

  18. Pan, S.M., Wen, R.H., Zhou, Z.H., Zhou, N.R.: Optical multi-image encryption scheme based on discrete cosine transform and nonlinear fractional Mellin transform. Multimed. Tools Appl. 76(2), 2933–2953 (2017)

    Article  Google Scholar 

  19. Klappenecker, A., Rotteler, M.: Discrete cosine transforms on quantum computers. Quantum Phys. 2(11), 464–468 (2001)

    Google Scholar 

  20. Li, X.Z., Chen, W.W., Wang, Y.Q.: Quantum image compression-encryption scheme based on quantum discrete cosine transform. Int. J. Theor. Phys. 57(9), 2904–2919 (2018)

    Article  MATH  Google Scholar 

  21. Chen, K.H., Yan, F., Abdullah, M.I., Zhao, J.P.: Dual quantum audio watermarking schemes based on quantum discrete cosine transform. Int. J. Theor. Phys. 58, 502–521 (2019)

    Article  MATH  Google Scholar 

  22. Jiang, N., Wen, Y.W., Wang, L.: The quantum realization of Arnold and Fibonacci image scrambling. Quantum Inf. Process. 13(5), 1223–1236 (2014)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  23. Zhou, N.R., Hua, T.X., Gong, L.H., Pei, D.J., Liao, Q.H.: Quantum image encryption based on generalized Arnold transform and double random-phase encoding. Quantum Inf. Process. 14(4), 1193–1213 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  24. Zhou, N.R., Hu, Y.Q., Gong, L.H., Li, G.Y.: Quantum image encryption scheme with iterative generalized Arnold transforms and quantum image cycle shift operations. Quantum Inf. Process. 16(6), 164 (2017)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  25. Hou, C.G., Liu, X.B., Feng, S.Y.: Quantum image scrambling algorithm based on discrete Baker map. Mod. Phys. Lett. A 35(17), 2050145 (2020)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  26. Zhou, N.R., Huang, L.X., Gong, L.H., Zeng, Q.W.: Novel quantum image compression and encryption algorithm based on DQWT and 3D hyper-chaotic Henon map. Quantum Inf. Process. 19(9), 284 (2020)

    Article  ADS  MathSciNet  Google Scholar 

  27. Gong, L.H., He, X.T., Cheng, S., Hua, T.X., Zhou, N.R.: Quantum image encryption algorithm based on quantum image XOR operations. Int. J. Theor. Phys. 55(7), 3234–3250 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  28. Liang, H.R., Tao, X.Y., Zhou, N.R.: Quantum image encryption based on generalized affine transform and logistic map. Quantum Inf. Process. 15(7), 2701–2724 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  29. Ran, Q.W., Wang, L., Ma, J., Tan, L.Y., Yu, S.Y.: A quantum color image encryption scheme based on coupled hyper-chaotic Lorenz system with three impulse injections. Quantum Inf. Process. 17(8), 188 (2018)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  30. Zhou, N.R., Chen, W.W., Yan, X.Y., Wang, Y.Q.: Bit-level quantum color image encryption scheme with quantum cross-exchange operation and hyper-chaotic system. Quantum Inf. Process. 17(6), 137 (2018)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  31. Musanna, F., Kumar, S.: Image encryption using quantum 3-D Baker map and generalized gray code coupled with fractional Chen’s chaotic system. Quantum Inf. Process. 19(8), 220 (2020)

    Article  ADS  MathSciNet  Google Scholar 

  32. Pang, C.Y., Zhou, R.G., Hu, B.Q., Hu, W.W., El-Rafei, A.: Signal and image compression using quantum discrete cosine transform. Inf. Sci. 473, 121–141 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  33. Jiang, N., Lu, X.W., Hu, H., Dang, Y.J., Cai, Y.Q.: A novel quantum image compression method based on JPEG. Int. J. Theor. Phys. 57(3), 611–636 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  34. Rössler, O.E., Klein, M., Baier, G., Parisi, J., Hudson, J.L.: Sierpin´ski sponge in a simple generic diffeomorphism. Comput. Phys. 4(5), 494–498 (1990)

    Article  ADS  Google Scholar 

  35. Vedral, V., Barenco, A., Ekert, A.: Quantum networks for elementary arithmetic operations. Physics Review A 54(1), 147 (1996)

    Article  ADS  MathSciNet  Google Scholar 

  36. Lu, X.W., Jiang, N., Hu, H., Dang, Y.J., Cai, Y.Q.: Quantum adder for superposition states. Int. J. Theor. Phys. 57(9), 2575–2584 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  37. Li, H.S., Fan, P., Xia, H., Long, G.L.: Efficient quantum arithmetic operation circuits for quantum image processing. Sci. China Phys. Mech. Astron. 63(8), 280311 (2020)

    Article  ADS  Google Scholar 

  38. Wang, J., Geng, Y.C., Han, L., Liu, J.Q.: Quantum image encryption algorithm based on quantum key image. Int. J. Theor. Phys. 58(1), 308–322 (2019)

    Article  MATH  Google Scholar 

  39. Mohimani, H., Babaie-Zadeh, M., Jutten, C.: A Fast Approach for overcomplete sparse decomposition based on smoothed l-0 norm. IEEE Trans. Signal Process. 57(1), 289–301 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  40. Luo, Y.L., Lin, J., Liu, J.X., Wei, D.Q., Cao, L.C., Zhou, R.L., Cao, Yi., Ding, X.M.: A robust image encryption algorithm based on Chua’s circuit and compressive sensing. Signal Process. 161, 227–247 (2019)

    Article  Google Scholar 

  41. Zhou, N.R., Yan, X.Y., Liang, H.R., Tao, X.Y., Gong, L.H.: Multi-image encryption scheme based on quantum 3D Arnold transform and scaled Zhongtang chaotic system. Quantum Inf. Process. 17(12), 338 (2018)

    Article  ADS  MATH  Google Scholar 

  42. Hu, Y.Q., Xie, X.W., Liu, X.B., Zhou, N.R.: Quantum multi-image encryption based on iteration Arnold transform with parameters and image correlation decomposition. Int. J. Theor. Phys. 56(7), 2192–2205 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  43. Chen, J.X., Zhu, Z.L., Fu, C., Yu, H.: A fast image encryption scheme with a novel pixel swapping-based confusion approach. Nonlinear Dyn. 77(4), 1191–1207 (2014)

    Article  Google Scholar 

  44. Bhatnagar, G., Wu, Q.M.J., Raman, B.: Discrete fractional wavelet transform and its application to multiple encryption. Inf. Sci. 223, 297–316 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  45. Ralph, T.C., Resch, K.J., Gilchrist, A.: Efficient Toffoli gates using qubits. Phys. Rev. A 75(2), 441–445 (2008)

    Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant Nos. 61462061, 61861029), the Major Academic Discipline and Technical Leader of Jiangxi Province (Grant No. 20162BCB22011), the Natural Science Foundation of Jiangxi Province (Grant No. 20171BAB202002), the Top double 1000 Talent Programme of Jiangxi Province (Grant No. JXSQ2019201055), and the Innovation Special Foundation of Graduate Student of Jiangxi Province (Grant No. YC2020-S104).

Author information

Authors and Affiliations

  1. Department of Electronic Information Engineering, Nanchang University, Nanchang, 330031, China

    Jing-Yi Dai, Yan Ma & Nan-Run Zhou

Authors
  1. Jing-Yi Dai
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yan Ma
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Nan-Run Zhou
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Nan-Run Zhou.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dai, JY., Ma, Y. & Zhou, NR. Quantum multi-image compression-encryption scheme based on quantum discrete cosine transform and 4D hyper-chaotic Henon map. Quantum Inf Process 20, 246 (2021). https://doi.org/10.1007/s11128-021-03187-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-021-03187-w

Keywords