Hierarchical remote preparation of an arbitrary two-qubit state with multiparty

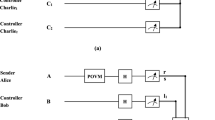
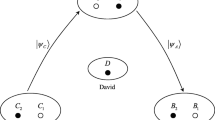
Abstract

Hierarchical remote preparation of an arbitrary two-qubit state has not been investigated by the previous work. We first put forward two deterministic schemes to realize the task among three agents by using two five-qubit cluster states as the quantum channel. To design these schemes, some useful and general measurement bases are constructed for the sender. Then, the two schemes are extended to multiparty with the aid of the symmetry of cluster state. There exists a hierarchy among the agents in terms of their ability to reconstruct the target state. The upper-grade agent requires the help of all the remaining upper-grade agents and anyone of the lower-grade agents. While the lower-grade agent needs the assistance of all the other agents. Finally, we consider the effect of two important decoherence noises: the amplitude-damping noise and phase-damping noise.

Appendix

Take the first HRSP scheme with three agents as example, we calculate the output state of the upper-grade agent Bob under the AD noise in detail.

The effect on the shared channel $\rho$ under the AD noise is

$$\begin{aligned} \varepsilon _a(\rho )= & {} \frac{1}{16}\{[|0000\rangle (|000000\rangle +\sqrt{{\tilde{\uplambda }}^3}(|010101\rangle +|101010\rangle ) +{\tilde{\uplambda }}^3|111111\rangle )\\&+\sqrt{{\tilde{\uplambda }}}|0101\rangle (|010000\rangle -\sqrt{{\tilde{\uplambda }}}|000101\rangle +\sqrt{{\tilde{\uplambda }}^3}|111010\rangle -{\tilde{\uplambda }}^2|101111\rangle )\\&+\sqrt{{\tilde{\uplambda }}}|1010\rangle (|100000\rangle +\sqrt{{\tilde{\uplambda }}^3}|110101\rangle -\sqrt{{\tilde{\uplambda }}}|001010\rangle -{\tilde{\uplambda }}^2|011111\rangle )\\&+{\tilde{\uplambda }}|1111\rangle (|110000\rangle -\sqrt{{\tilde{\uplambda }}}(|100101\rangle +|011010\rangle )+{\tilde{\uplambda }}|001111\rangle )]\\&\times [\langle 0000|(\langle 000000|+\sqrt{{\tilde{\uplambda }}^3}(\langle 010101|+\langle 101010|) +{\tilde{\uplambda }}^3\langle 111111|)\\&+\sqrt{{\tilde{\uplambda }}}\langle 0101|\langle 010000|-\sqrt{{\tilde{\uplambda }}}\langle 000101| +\sqrt{{\tilde{\uplambda }}^3}\langle 111010|-{\tilde{\uplambda }}^2\langle 101111|)\\&+\sqrt{{\tilde{\uplambda }}}\langle 1010|(\langle 100000|+\sqrt{{\tilde{\uplambda }}^3}\langle 110101| -\sqrt{{\tilde{\uplambda }}}\langle 001010|-{\tilde{\uplambda }}^2\langle 011111|)\\&+{\tilde{\uplambda }}\langle 1111|(\langle 110000|-\sqrt{{\tilde{\uplambda }}}(\langle 100101| +\langle 011010|)+{\tilde{\uplambda }}\langle 001111|)]\\&+\uplambda ^4[{\tilde{\uplambda }}|0000\rangle |11\rangle -\sqrt{{\tilde{\uplambda }}}(|0101\rangle |10\rangle +|1010\rangle |01\rangle )+|1111\rangle |00\rangle ]|0000\rangle \\&\times [{\tilde{\uplambda }}\langle 0000|\langle 11|-\sqrt{{\tilde{\uplambda }}}(\langle 0101|\langle 10| +\langle 1010|\langle 01|)+\langle 1111|\langle 00|]\langle 0000|]\\&+\uplambda ^2({\tilde{\uplambda }}^2|0000\rangle |001111\rangle +{\tilde{\uplambda }}|0101\rangle |001010\rangle +{\tilde{\uplambda }}|1010\rangle |000101\rangle \\&+|1111\rangle |000000\rangle )\times ({\tilde{\uplambda }}^2\langle 0000|\langle 001111| +{\tilde{\uplambda }}\langle 0101|\langle 001010|\\&+{\tilde{\uplambda }}\langle 1010|\langle 000101|+\langle 1111|\langle 000000|)+\uplambda ^6|0000000000\rangle \langle 0000000000|\}. \end{aligned}$$

For simple but without loss of generality, assume Alice’s first-step measurement result is $|\xi _{00}\rangle _\mathrm{A_{11}A_{21}}$, the system of qubits $(\mathrm A_{12},A_{22},B_{11},B_{21},C_{11},C_{21},C_{12},C_{22})$ becomes

$$\begin{aligned} \rho _1= & {} \frac{1}{16P_1}\{[r_0|00\rangle (|000000\rangle +\sqrt{{\tilde{\uplambda }}^3}(|010101\rangle +|101010\rangle ) +{\tilde{\uplambda }}^3|111111\rangle )\\&+\sqrt{{\tilde{\uplambda }}}r_1|01\rangle (|010000\rangle -\sqrt{{\tilde{\uplambda }}}|000101\rangle +\sqrt{{\tilde{\uplambda }}^3}|111010\rangle -{\tilde{\uplambda }}^2|101111\rangle )\\&+\sqrt{{\tilde{\uplambda }}}r_2|10\rangle (|100000\rangle +\sqrt{{\tilde{\uplambda }}^3}|110101\rangle -\sqrt{{\tilde{\uplambda }}}|001010\rangle -{\tilde{\uplambda }}^2|011111\rangle )\\&+{\tilde{\uplambda }}r_3|11\rangle (|110000\rangle -\sqrt{{\tilde{\uplambda }}}(|100101\rangle +|011010\rangle ) +{\tilde{\uplambda }}|001111\rangle )]\\&\times [r_0\langle 00|(\langle 000000|+\sqrt{{\tilde{\uplambda }}^3}(\langle 010101|+\langle 101010|) +{\tilde{\uplambda }})^3\langle 111111|\\&+\sqrt{{\tilde{\uplambda }}}r_1\langle 01|(\langle 010000|-\sqrt{{\tilde{\uplambda }}}\langle 000101|+\sqrt{{\tilde{\uplambda }}^3}\langle 111010| -{\tilde{\uplambda }}^2\langle 101111|)\\&+\sqrt{{\tilde{\uplambda }}}r_2\langle 10|(\langle 100000|+\sqrt{{\tilde{\uplambda }}^3}\langle 110101|-\sqrt{{\tilde{\uplambda }}}\langle 001010| -{\tilde{\uplambda }}^2\langle 011111|)\\&+{\tilde{\uplambda }}r_3\langle 11|(\langle 110000|-\sqrt{{\tilde{\uplambda }}}(\langle 100101|+\langle 011010|)+{\tilde{\uplambda }}\langle 001111|)]\\&+\uplambda ^2[({\tilde{\uplambda }})^2r_0|00\rangle |001111\rangle +{\tilde{\uplambda }}(r_1|01\rangle |001010\rangle \\&+r_2|10\rangle |000101\rangle )+r_3|11\rangle |000000\rangle ]\\&\times [{\tilde{\uplambda }}^2r_0\langle 00|\langle 001111|+{\tilde{\uplambda }}(r_1\langle 01|\langle 001010|\\&+r_2\langle 10|\langle 000101|)+r_3\langle 11|\langle 000000|]\\&+\uplambda ^4[{\tilde{\uplambda }}r_0|00\rangle |110000\rangle -\sqrt{{\tilde{\uplambda }}}(r_1|01\rangle |100000\rangle \\&+r_2|10\rangle |010000\rangle )+r_3|11\rangle |000000\rangle ]\\&\times [{\tilde{\uplambda }}r_0\langle 00|\langle 110000|-\sqrt{{\tilde{\uplambda }}}(r_1\langle 01|\langle 100000|\\&+r_2\langle 10|\langle 010000|) +r_3\langle 11|\langle 000000|]\\&+\uplambda ^6r_0^2|00000000\rangle \langle 00000000|\}, \end{aligned}$$

where

$$\begin{aligned} P_1= & {} \mathrm{tr}\left( M_\mathrm{A}^{1^\dag }M_\mathrm{A}^1\varepsilon _a(\rho )\right) \\= & {} \frac{1}{16}\left\{ r_0^2\left[ \prod \limits _{j=1}^2(\uplambda ^{2j}+{\tilde{\uplambda }}^{2j})+2{\tilde{\uplambda }}^3+1\right] \right. \\&+{\tilde{\uplambda }}(r_1^2+r_2^2)[\uplambda ^4-\uplambda +2 +{\tilde{\uplambda }}^4+{\tilde{\uplambda }}^3+\uplambda ^2{\tilde{\uplambda }}]\\&\left. +r_3^2[\uplambda ^4+\uplambda ^2+{\tilde{\uplambda }}^2(2-\uplambda )^2]\right. \} \end{aligned}$$

is the probability that Alice gets the measurement result $|\xi _{00}\rangle _\mathrm{A_{11}A_{21}}$.

Alice performs the unitary operation $I_\mathrm{A_{12}}I_\mathrm{A_{22}}$ conditioned on her first-step measurement result. Then Alice measures her qubits $(\mathrm A_{12},A_{22})$ under the measurement basis in Eq. (12). If the measurement result $|\eta _{00}\rangle$, the qubits $(\mathrm B_{11},B_{21},C_{11},C_{21},C_{12},C_{22})$ collapse into

$$\begin{aligned} \rho _2= & {} \frac{1}{16P_1P_2}\{[\alpha _0(|000000\rangle +\sqrt{{\tilde{\uplambda }}^3}(|010101\rangle +|101010\rangle ) +{\tilde{\uplambda }}^3|111111\rangle )\\&+\sqrt{{\tilde{\uplambda }}}\alpha _1(|010000\rangle -\sqrt{{\tilde{\uplambda }}}|000101\rangle +\sqrt{{\tilde{\uplambda }}^3}|111010\rangle -{\tilde{\uplambda }}^2|101111\rangle )\\&+\sqrt{{\tilde{\uplambda }}}\alpha _2(|100000\rangle +\sqrt{{\tilde{\uplambda }}^3}|110101\rangle -\sqrt{{\tilde{\uplambda }}}|001010\rangle -{\tilde{\uplambda }}^2|011111\rangle )\\&+{\tilde{\uplambda }}\alpha _3(|110000\rangle -\sqrt{{\tilde{\uplambda }}}(|100101\rangle +|011010\rangle )+{\tilde{\uplambda }}|001111\rangle )]\\&\times [\alpha _0^*(\langle 000000|+\sqrt{{\tilde{\uplambda }}^3}(\langle 010101|+\langle 101010|)+{\tilde{\uplambda }}^3\langle 111111|)\\&+\sqrt{{\tilde{\uplambda }}}\alpha _1^*(\langle 010000|-\sqrt{{\tilde{\uplambda }}}\langle 000101|+\sqrt{{\tilde{\uplambda }}^3}\langle 111010| -{\tilde{\uplambda }}^2\langle 101111|)\\&+\sqrt{{\tilde{\uplambda }}}\alpha _2^*(\langle 100000|+\sqrt{{\tilde{\uplambda }}^3}\langle 110101|-\sqrt{{\tilde{\uplambda }}}\langle 001010| -{\tilde{\uplambda }}^2\langle 011111|)\\&+{\tilde{\uplambda }}\alpha _3^*(\langle 110000|-\sqrt{{\tilde{\uplambda }}}(\langle 100101|+\langle 011010|)+{\tilde{\uplambda }}\langle 001111|)]\\&+\uplambda ^2[{\tilde{\uplambda }}^2\alpha _0|001111\rangle +{\tilde{\uplambda }}(\alpha _1|001010\rangle +\alpha _2|000101\rangle ) +\alpha _3|000000\rangle ]\\&\times [{\tilde{\uplambda }}^2\alpha _0^*\langle 001111|+{\tilde{\uplambda }}(\alpha _1^*\langle 001010| +\alpha _2^*\langle 000101|)+\alpha _3^*\langle 000000|]\\&+\uplambda ^4[{\tilde{\uplambda }}\alpha _0|110000\rangle -\sqrt{{\tilde{\uplambda }}}(\alpha _1|100000\rangle +\alpha _2|010000\rangle )+\alpha _3|000000\rangle ]\\&\times [{\tilde{\uplambda }}\alpha _0^*\langle 110000|-\sqrt{{\tilde{\uplambda }}}(\alpha _1^*\langle 100000| +\alpha _2^*\langle 010000|)+\alpha _3^*\langle 000000|]\\&+\uplambda ^6|\alpha _0|^2|000000\rangle \langle 000000|, \end{aligned}$$

where

$$\begin{aligned} P_2= & {} \mathrm{tr}\left( M_\mathrm{A}^{2^\dag }M_\mathrm{A}^2\varepsilon _a(\rho _1)\right) \\= & {} \frac{1}{16P_1}\left\{ \left[ \prod \limits _{j=1}^2(\uplambda ^{2j}+{\tilde{\uplambda }}^{2j})+2{\tilde{\uplambda }}^3+1\right] |\alpha _0|^2\right. \\&+{\tilde{\uplambda }} (\uplambda ^4-\uplambda +2+{\tilde{\uplambda }}^4+{\tilde{\uplambda }}^3+\uplambda ^2{\tilde{\uplambda }})(|\alpha _1|^2+|\alpha _2|^2)\\&+[\uplambda ^4+\uplambda ^2+{\tilde{\uplambda }}^2(2-\uplambda )^2]|\alpha _3|^2\bigg \} \end{aligned}$$

is the probability that Alice gets the measurement result $|\eta _{00}\rangle _\mathrm{A_{12}A_{22}}$.

The agents consent the upper-grade agent Bob to recover the target state. Charlie$_1$ exerts single-qubit projective measurement on his qubit $\mathrm{C}_{11}$ under Z basis. If Charlie$_1$’s measurement outcome is $|0\rangle$, the system of qubits $(\mathrm B_{11},B_{21},C_{21},C_{12},C_{22})$ becomes

$$\begin{aligned} \rho _3= & {} \frac{1}{16P_1P_2P_3}\left\{ [\alpha _0(|00000\rangle +\sqrt{{\tilde{\uplambda }}^3}|01101\rangle ) +\sqrt{{\tilde{\uplambda }}}\alpha _1(|01000\rangle -\sqrt{{\tilde{\uplambda }}}|00101\rangle )\right. \\&+\sqrt{{\tilde{\uplambda }}}\alpha _2(|10000\rangle +\sqrt{{\tilde{\uplambda }}^3}|11101\rangle ) +{\tilde{\uplambda }}\alpha _3(|11000\rangle -\sqrt{{\tilde{\uplambda }}}|10101\rangle )]\\&\times [\alpha _0^*(\langle 00000|+\sqrt{{\tilde{\uplambda }}^3}\langle 01101|) +\sqrt{{\tilde{\uplambda }}}\alpha _1^*(\langle 01000|-\sqrt{{\tilde{\uplambda }}}\langle 00101|)\\&+\sqrt{{\tilde{\uplambda }}}\alpha _2^*(\langle 10000|+\sqrt{{\tilde{\uplambda }}^3}\langle 11101|) +{\tilde{\uplambda }}\alpha _3^*(\langle 11000|-\sqrt{{\tilde{\uplambda }}}\langle 10101|)]\\&+\uplambda ^2({\tilde{\uplambda }}\alpha _2|00101\rangle +\alpha _3|00000\rangle ) \times ({\tilde{\uplambda }}\alpha _2^*\langle 00101|+\alpha _3^*\langle 00000|)\\&+\uplambda ^4[{\tilde{\uplambda }}\alpha _0|11000\rangle -\sqrt{{\tilde{\uplambda }}}(\alpha _1|10000\rangle +\alpha _2|01000\rangle )+\alpha _3|00000\rangle ]\\&\times [{\tilde{\uplambda }}\alpha _0^*\langle 11000|-\sqrt{{\tilde{\uplambda }}}(\alpha _1^*\langle 10000| +\alpha _2^*\langle 01000|)+\alpha _3^*\langle 00000|]\\&+\uplambda ^6|\alpha _0|^2|00000\rangle \langle 00000|, \end{aligned}$$

where

$$\begin{aligned} P_3= & {} \mathrm{tr}\left( M_{\mathrm{C}_1}^{3^\dag }M_{\mathrm{C}_1}^3\rho _2\right) \\= & {} \frac{1}{16P_1P_2}\left\{ |\alpha _0|^2(\uplambda ^6+\uplambda ^4{\tilde{\uplambda }}^2+{\tilde{\uplambda }}^3+1) +|\alpha _1|^2{\tilde{\uplambda }}(\uplambda ^4-\uplambda +2)\right. \\&\left. +|\alpha _2|^2{\tilde{\uplambda }} (\uplambda ^4-\uplambda ^2+\uplambda +{\tilde{\uplambda }}^3+1)+|\alpha _3|^2[\uplambda ^4+\uplambda ^2+{\tilde{\uplambda }}^2(\uplambda -2)^2]\right\} \end{aligned}$$

is the probability that Charlie$_1$ gets the measurement result $|0\rangle _\mathrm{C_{11}}$.

Charlie$_1$ preforms single-qubit projective measurements on his qubit $\mathrm{C}_{21}$ under the basis $\{|0\rangle ,|1\rangle \}$. If Charlie$_1$’s measurement outcome is $|0\rangle$, the system of qubits $(\mathrm B_{11},B_{21},C_{12},C_{22})$ becomes

$$\begin{aligned} \rho _4= & {} \frac{1}{16P_1P_2P_3P_4}\left\{ [\alpha _0|00\rangle +\sqrt{{\tilde{\uplambda }}}(\alpha _1|01\rangle +\alpha _2|10\rangle )+\alpha _3{\tilde{\uplambda }}|11\rangle ]|00\rangle \right. \\&\times [\alpha _0^*\langle 00|+\sqrt{{\tilde{\uplambda }}}(\alpha _1^*\langle 01| +\alpha _2^*\langle 10|)+\alpha _3^*{\tilde{\uplambda }}\langle 11|]\langle 00| +\uplambda ^2|\alpha _3|^2|0000\rangle \langle 0000|\\&+\uplambda ^4[{\tilde{\uplambda }}\alpha _0|11\rangle -\sqrt{{\tilde{\uplambda }}}(\alpha _1|10\rangle +\alpha _2|01\rangle )+\alpha _3|00\rangle ]|00\rangle \\&\left. \times [{\tilde{\uplambda }}\alpha _0^*\langle 11|-\sqrt{{\tilde{\uplambda }}}(\alpha _1^*\langle 10| +\alpha _2^*\langle 01|)+\alpha _3^*\langle 00|]\langle 00| +\uplambda ^6|\alpha _0|^2|0000\rangle \langle 0000|\right\} , \end{aligned}$$

where

$$\begin{aligned} P_4= & {} \mathrm{tr}\left( M_{\mathrm{C}_1}^{4^\dag }M_{\mathrm{C}_1}^4\rho _3\right) \\= & {} \frac{1}{16P_1P_2P_3}[{\tilde{\uplambda }}(\uplambda ^4+1) -\uplambda ^5(2\uplambda -1)|\alpha _0|^2 +\uplambda (\uplambda ^4+2\uplambda -1)|\alpha _3|^2] \end{aligned}$$

is the probability that Charlie$_1$ gets the measurement result $|0\rangle _\mathrm{C_{21}}$.

According to Alice’s and Charlie$_1$’s measurement results, Bob performs recovery operation $I_\mathrm{B_{11}}I_\mathrm{B_{21}}$ and gets the output state in Eq. (47).