Skip to main content
SpringerLink
Log in

Quantum correlations of tripartite entangled states under Gaussian noise

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

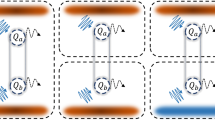
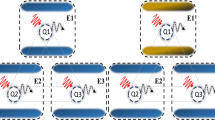
We investigate the preservation of quantum coherence and entanglement carried by the three non-interacting qubits during their evolution in the presence of an external fluctuating field characterized by a classical Gaussian noise. Initially, the three non-interacting qubits are considered in two different maximally entangled states, namely Greenberger–Horne–Zeilinger (\(\mathcal {X}_{G}\)) and Werner \((\mathcal {X}_{W})\) state. Besides this, we study the time evolution of the two states in three different schemes, namely: common, mixed, and independent system–environment couplings. By deploying different measures, we show that the system–environment coupling and the Gaussian noise greatly affected the quantum correlation and coherence. We also found that the non-local correlation and coherence remain more dominant and robust in common system–environment coupling for the \(\mathcal {X_G}\) state under the Gaussian noise. Hence, this kind of feature of the \(\mathcal {X}_{G}\) state is a vital resource for the transmission of quantum information with reduced loss.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Maziero, J., Celeri, L.C., Serra, R.M., Vedral, V.: Classical and quantum correlations under decoherence. Phys. Rev. A 80(4), 044102 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  2. Adesso, G., Bromley, T.R., Cianciaruso, M.: Measures and applications of quantum correlations. J. Phys. A Math. Theor. 49(47), 473001 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  3. Khalid, U., ur Rehman, J., Shin, H.: Measurement-based quantum correlations for quantum information processing. Sci. Rep. 10(1), 1–8 (2020)

    Article  Google Scholar 

  4. Horodecki, R., Horodecki, P., Horodecki, M., Horodecki, K.: Quantum entanglement. Rev. Mod. Phys. 81(2), 865–942 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  5. Raamsdonk, V.: Building up spacetime with quantum entanglement. Gen. Relat. Gengrav. 42(10), 2323–2329 (2010)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  6. Karlsson, A., Koashi, M., Imoto, N.: Quantum entanglement for secret sharing and secret splitting. Phy. Rev. A 59(1), 162–168 (1999)

    Article  ADS  Google Scholar 

  7. Boyer, M., Brodutch, A., Mor, T.: Entanglement and deterministic quantum computing with one qubit. Phys. Rev. A 95(2), 022330 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  8. Treiber, A., Poppe, A., Hentschel, M., Ferrini, D., Lorünser, T., Querasser, E., Zeilinger, A.: A fully automated entanglement-based quantum cryptography system for telecom fiber networks. New J. Phys. 11(4), 045013 (2009)

    Article  ADS  Google Scholar 

  9. Braunstein, S.L., Kimble H.J.: Dense coding for continuous variables. In: Quantum Information with Continuous Variables, pp. 95–103. Springer, Dordrecht (2000)

  10. Murao, M., Jonathan, D., Plenio, M.B., Vedral, V.: Quantum telecloning and multiparticle entanglement. Phys. Rev. A 59(1), 156 (1999)

    Article  ADS  Google Scholar 

  11. Ghasemi, M., Tavassoly, M.K., Nourmandipour, A.: Dissipative entanglement swapping in the presence of detuning and Kerr medium: Bell state measurement method. Eur. Phys. J. Plus 132(12), 1–10 (2017)

    Article  Google Scholar 

  12. Supic, I., Skrzypczyk, P., Cavalcanti, D.: Methods to estimate entanglement in teleportation experiments. Phys. Rev. A 99(3), 032334 (2019)

    Article  ADS  Google Scholar 

  13. Datta, S.: Quantum devices. Superlattices Microstruct. 6(1), 83–93 (1989)

    Article  ADS  Google Scholar 

  14. Oh, S., Lee, S., Lee, H.W.: Fidelity of quantum teleportation through noisy channels. Phys. Rev. A 66(2), 022316–022316 (2002)

    Article  ADS  MathSciNet  Google Scholar 

  15. Grosshans, F., Cerf, N., Wenger, J., Tualle-Brouri, R., Grangier, P.: Virtual entanglement and reconciliation protocols for quantum cryptography with continuous variables. Quant. Inf. Comp. 3(7), 535–552 (2003)

    MathSciNet  MATH  Google Scholar 

  16. Mattle, K., Weinfurter, H., Kwiat, P.G., Zeilinger, A.: Dense coding in experimental quantum communication. Phy. Rev. lett. 76(25), 4656–4659 (1996)

    Article  ADS  Google Scholar 

  17. Lo, H.K., Curty, M., Tamaki, K.: Secure quantum key distribution. Nat. Photon. 8, 595–604 (2014)

    Article  ADS  Google Scholar 

  18. Lo, H.K., Chau, H.F.: Unconditional security of quantum key distribution over arbitrarily long distances. Science 283(5410), 2050–2056 (1999)

    Article  ADS  Google Scholar 

  19. Leibfried, D., Knill, E., Seidelin, S., Britton, J., Blakestad, R.B., Chiaverini, J., Ozeri, R.: Creation of a six-atom ‘Schrödinger cat’state. Nature 438(7068), 639–642 (2005)

  20. Lu, C.Y., Zhou, X.Q., Gühne, O., Gao, W.B., Zhang, J., Yuan, Z.S., Goebel, A., Yang, T., Pan, J.W.: Experimental entanglement of six photons in graph states. Nat. Phys. 3, 91–95 (2007)

    Article  Google Scholar 

  21. Hald, J., Sörensen, J.L., Schori, C., Polzik, E.S.: Spin squeezed atoms: a macroscopic entangled ensemble created by light. Phys. Rev. Lett. 83, 1319–1322 (1999)

    Article  ADS  Google Scholar 

  22. Mandel, O., Greiner, M., Widera, A., Rom, T., Hänsch, T., Bloch, I.: Controlled collisions for multi-particle entanglement of optically trapped atoms. Nature 425, 937–940 (2003)

    Article  ADS  Google Scholar 

  23. Viola, L., Lloyd, S.: Dynamical suppression of decoherence in two-state quantum systems. Phys. Rev. A. 58(4), 2733–2744 (1998)

    Article  ADS  MathSciNet  Google Scholar 

  24. Almeida, M.P., de Melo, F., Hor-Meyll, M., Salles, A., Walborn, S.P., Ribeiro, P.S., Davidovich, L.: Environment-induced sudden death of entanglement. Science 316(5824), 579–582 (2007)

    Article  ADS  Google Scholar 

  25. Javed, M., Khan, S., Ullah, S.A.: The dynamics of quantum correlations in mixed classical environments. J. Russ. Laser Res. 37(6), 562–571 (2016)

    Article  Google Scholar 

  26. Chen, K., Albeverio, S., Fei, S.M.: Concurrence of arbitrary dimensional bipartite quantum states. Phys. Rev. Lett. 95(4), 040504 (2005)

    Article  ADS  MathSciNet  Google Scholar 

  27. Pan, J.W.: Experimental test of quantum non-locality in three-photon Greenberger–Horne–Zeilinger entanglement. Nature 403, 515–519 (1997)

    Article  ADS  Google Scholar 

  28. Carvalho, A.R., Mintert, A.F.: Buchleitner decoherence and multipartite entanglement. Phys. Rev. Lett. 93(23), 230501–230501 (2004)

    Article  ADS  Google Scholar 

  29. Hauke, P., Heyl, M., Tagliacozzo, L., Zoller, P.: Measuring multipartite entanglement through dynamic susceptibilities. Nat. Phys. 12(8), 778–782 (2016)

    Article  Google Scholar 

  30. Mandelbrot, B.B., Wallis, J.R.: Computer experiments with fractional Gaussian noises: part 1, averages and variances. Water Resour. Res. 5(1), 228–241 (1969)

    Article  ADS  Google Scholar 

  31. Fuentes, M.A., Toral, R., Wio, H.S.: Enhancement of stochastic resonance: the role of non Gaussian noises. Physica A 295(1–2), 114–122 (2001)

    Article  ADS  MATH  Google Scholar 

  32. Lansky, P., Sacerdote, L.: The Ornstein–Uhlenbeck neuronal model with signal-dependent noise. Phys. Lett. A 285(3–4), 132–140 (2001)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  33. Lohstroh, J.: Static and dynamic noise margins of logic circuits. IEEE J. Solid-State Circuits 14(3), 591–598 (1979)

    Article  ADS  Google Scholar 

  34. Makra, P., Gingl, Z., Fülei, T.: Signal-to-noise ratio gain in stochastic resonators driven by coloured noises. Phys. Lett. A 317(3–4), 228–232 (2003)

    Article  ADS  MATH  Google Scholar 

  35. Wang, B., Xu, Z., Chen, Z., Feng, M.: Non-Markovian effect on the quantum discord. Phy. Rev. A 81(1), 014101–014101 (2010)

    Article  ADS  Google Scholar 

  36. Lo Franco, R., Bellomo, B., Maniscalco, S., Compagno, G.: Dynamics of quantum correlations in two-qubit systems within non-Markovian environments. Int. J. Mod. Phys. B 27, 1345053–1345072 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  37. Benedetti, C., Paris, M.G.: Characterization of classical Gaussian processes using quantum probes. Phys. Lett. A. 378(34), 2495–2500 (2014)

    Article  ADS  MATH  Google Scholar 

  38. Laflamme, R., Knill, E., Zurek, W.H., Catasti, P., Mariappan, S.V.S.: NMR Greenberger–Horne–Zeilinger states. Philos. Trans. R. Soc. Lond. A. 356, 1941–1948 (1998)

    Article  ADS  MathSciNet  Google Scholar 

  39. Pan, J.W., Zeilinger, A.: Greenberger–Horne–Zeilinger state analyzer. Phys. Rev. A. 57(3), 2208–2211 (1998)

    Article  ADS  MathSciNet  Google Scholar 

  40. Lee, J., Kim, M.S.: Entanglement teleportation via Werner states. Phys. Rev. Lett. 84(18), 4236–4239 (2000)

    Article  ADS  Google Scholar 

  41. Brandao, F.G.: Quantifying entanglement with witness operators. Phys. Rev. A. 72(2A), 022310–1 (2005)

    Article  ADS  MathSciNet  Google Scholar 

  42. Ann, K., Jaeger, G.: Disentanglement and decoherence in two-spin and three-spin systems under dephasing. Phys. Rev. B 75(11), 115307 (2007)

    Article  ADS  Google Scholar 

  43. Fabrice, K.F., Arthur, T.T., Pernel, N.N., Martin, T., Fai, L.C.: Tripartite quantum discord dynamics in qubits driven by the joint influence of distinct classical noises. Quant. Inf. Process. 20(1), 1–15 (2021)

    Article  MathSciNet  Google Scholar 

  44. Dodonov, V.V.: Purity-and entropy-bounded uncertainty relations for mixed quantum states. J. Opt. B Quant. Semiclass. Opt. 4(3), S98–S108 (2002)

    Article  ADS  MathSciNet  Google Scholar 

  45. Mazzola, L., Pilao, J., Maniscalo Sudden, S.: Transition between classical and quantum decoherence. Phys. Rev. Lett. 104(20), 200401–200401 (2010)

    Article  ADS  MathSciNet  Google Scholar 

  46. Kenfack, L.T., Tchoffo, M., Fai, L.C., Fouokeng, G.C.: Decoherence and tripartite entanglement dynamics in the presence of Gaussian and non-Gaussian classical noise. Physica B 511, 123–133 (2017)

    Article  ADS  Google Scholar 

  47. Roos, C.F., Riebe, M., Häffner, H., Hänsel, W., Benhelm, J., Lancaster, G.P., Blatt, R.: Control and measurement of three-qubit entangled states. Science 304(5676), 1478–1480 (2004)

    Article  ADS  Google Scholar 

  48. Siewert, J., Eltschka, C.: Quantifying tripartite entanglement of three-qubit generalized Werner states. Phys. Rev. Lett. 108(23), 230502 (2012)

    Article  ADS  Google Scholar 

  49. Werner, R.F.: Quantum states with Einstein–Podolsky–Rosen correlations admitting a hidden-variable model. Phys. Rev. A 40, 4277 (1989)

    Article  ADS  MATH  Google Scholar 

  50. Rossi, M.A., Paris, M.G.: Non-Markovian dynamics of single-and two-qubit systems interacting with Gaussian and non-Gaussian fluctuating transverse environments. J. Chem. Phys. 144(2), 024113 (2016)

    Article  ADS  Google Scholar 

  51. Tsokeng, A.T., Tchoffo, M., Fai, L.C.: Dynamics of entanglement and quantum states transitions in spin-qutrit systems under classical dephasing and the relevance of the initial state. J. Phys. Commun. 2(3), 035031 (2018)

    Article  MATH  Google Scholar 

  52. Svetlichny, G.: Distinguishing three-body from two-body non-separability by a Bell-type inequality. Phys. Rev. D 35, 3066 (1987)

    Article  ADS  MathSciNet  Google Scholar 

  53. Clivaz, F., Huber, M., Lami, L., Murta, G.: Genuine-multipartite entanglement criteria based on positive maps. J. Math. Phys. 58(8), 082201 (2017)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  54. Bourennane, M., Eibl, M., Kurtsiefer, C., Gaertner, S., Weinfurter, H., Gühne, O., Sanpera, A.: Experimental detection of multipartite entanglement using witness operators. Phys. Rev. Lett. 92(8), 087902 (2004)

    Article  ADS  Google Scholar 

  55. Branciard, C., Rosset, D., Liang, Y.C., Gisin, N.: Measurement-device-independent entanglement witnesses for all entangled quantum states. Phys. Rev. Lett. 110(6), 060405 (2013)

    Article  ADS  Google Scholar 

  56. Bhattacharya, S.S., Paul, B., Roy, A., Mukherjee, A., Jebaratnam, C., Banik, M.: Improvement in device-independent witnessing of genuine tripartite entanglement by local marginals. Phys. Rev. A 95(4), 042130 (2017)

    Article  ADS  Google Scholar 

  57. Xu, P., Yuan, X., Chen, L.K., Lu, H., Yao, X.C., Ma, X., Pan, J.W.: Implementation of a measurement-device-independent entanglement witness. Phys. Rev. Lett. 112(14), 140506 (2014)

    Article  ADS  Google Scholar 

  58. Tchoffo, M., Kenfack, L.T., Fouokeng, G.C., Fai, L.C.: Quantum correlations dynamics and decoherence of a three-qubit system subject to classical environmental noise. Eur. Phys. J. Plus 10(131), 1–18 (2016)

    Google Scholar 

  59. Islam, R., Ma, R., Preiss, P.M., Eric Tai, M., Lukin, A., Rispoli, M., Greiner, M.: Measuring entanglement entropy in a quantum many-body system. Nature 528, 77–83 (2015)

    Article  ADS  Google Scholar 

  60. Ziman, M., Buzek, V.: Concurrence versus purity: influence of local channels on Bell states of two qubits. Phys. Rev. A 72(5), 052325 (2005)

    Article  ADS  Google Scholar 

  61. Tolkunov, D., Privman, V., Aravind, P.K.: Decoherence of a measure of entanglement. Phys. Rev. A 71(6), 060308 (2005)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  62. Bellomo, B., Franco, R.L., Compagno, G.: Non-Markovian effects on the dynamics of entanglement. Phys. Rev. Lett. 99(16), 160502 (2007)

    Article  ADS  Google Scholar 

  63. Fanchini, F.F., Werlang, T., Brasil, C.A., Arruda, L.G.E., Caldeira, A.O.: Non-Markovian dynamics of quantum discord. Phys. Rev. A 81(5), 052107 (2010)

    Article  ADS  Google Scholar 

  64. Benedetti, C., Buscemi, F., Bordone, P., Paris, M.G.: Dynamics of quantum correlations in colored-noise environments. Phys. Rev. A 87(5), 052328 (2013)

    Article  ADS  Google Scholar 

  65. Buscemi, F., Bordone, P.: Time evolution of tripartite quantum discord and entanglement under local and non-local random telegraph noise. Phys. Rev. A 87(4), 042310 (2013)

    Article  ADS  Google Scholar 

  66. Tsokeng, A.T., Tchoffo, M., Fai, L.C.: Quantum correlations and decoherence dynamics for a qutrit- qutrit system under random telegraph noise. Quant. Inf. Process. 16(8), 191 (2017)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  67. Kenfack, L.T., Tchoffo, M., Javed, M., Fai, L.C.: Dynamics and protection of quantum correlations in a qubit qutrit system subjected locally to a classical random field and colored noise. Quant. Inf. Process. 19(4), 107 (2020)

    Article  ADS  MathSciNet  Google Scholar 

  68. Guo, J.L., Wei, J.L.: Dynamics and protection of tripartite quantum correlations in a thermal bath. Ann. Phys. 354, 522–533 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  69. Lionel, T.K., Martin, T., Collince, F.G., Fai, L.C.: Effects of static noise on the dynamics of quantum correlations for a system of three qubits. Int. J. Mod. Phys. B 31(8), 1750046 (2017)

    Article  ADS  MATH  Google Scholar 

  70. Tchoffo, M., Kenfack, L.T., Fouokeng, G.C., Fai, L.C.: Quantum correlations dynamics and decoherence of a three-qubit system subject to classical environmental noise. Eur. Phys. J. Plus 131(10), 380 (2016)

    Article  Google Scholar 

  71. Rossi, M.A., Benedetti, C., Paris, M.G.: Engineering decoherence for two-qubit systems interacting with a classical environment. Int. J. Quant. Inf. 12(07–08), 1560003 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  72. Siomau, M., Fritzsche, S.: Entanglement dynamics of three-qubit states in noisy channels. Eur. Phys. J. D 60(2), 397–403 (2010)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Quantum Optics and Quantum Information Research Group, Department of Physics, University of Malakand, Chakdara Dir, Pakistan

    Atta Ur Rahman, Muhammad Noman, Muhammad Javed & Arif Ullah

  2. The School of Information Science and Technology, Southwest Jiaotong University, Chengdu, 610031, China

    Ming-Xing Luo

Authors
  1. Atta Ur Rahman
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Muhammad Noman
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Muhammad Javed
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ming-Xing Luo
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Arif Ullah
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Arif Ullah.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

This section describes the detailed numerical simulations that are carried out for the time evolution for the \(\mathcal {X}_{G}\) and \(\mathcal {X}_{W}\) states under \(\mathcal {G_N}\) noise for the ces, mes and ies configurations.

1.1 Appendix 1. The case of common environment setup

Using Eq. 8 for ces model, we get the final density matrix after taking the average of the time-evolved density matrix for the \(\mathcal {X_G}\) state over the noise phase, and we get:

$$\begin{aligned} \rho _{ces}^{\mathcal {X}_G }(\varphi _1, \tau )=\left[ \begin{array}{cccccccc} h_{1} &{}\quad h_{2} &{}\quad h_{2} &{}\quad h_{2} &{}\quad h_{2} &{}\quad h_{2} &{}\quad h_{2} &{}\quad h_{1} \\ h_{2} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{2} \\ h_{2} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{2} \\ h_{2} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{2} \\ h_{2} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{2} \\ h_{2} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{2} \\ h_{2} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{3} &{}\quad h_{2} \\ h_{1} &{}\quad h_{2} &{}\quad h_{2} &{}\quad h_{2} &{}\quad h_{2} &{}\quad h_{2} &{}\quad h_{2} &{}\quad h_{1} \end{array} \right] , \end{aligned}$$
(32)

Similarly, by using the final density matrix for \(\mathcal {X}_{W}\) state given in Eq. (8) for ces configuration, we get:

$$\begin{aligned} \rho _{ces}^{\mathcal {X}_W}(\varphi _1, \tau )=\left[ \begin{array}{cccccccc} h_{4} &{}\quad 0 &{}\quad 0 &{}\quad h_{5} &{}\quad 0 &{}\quad h_{5} &{}\quad h_{5} &{}\quad 0 \\ 0 &{}\quad h_{6} &{}\quad h_{6} &{}\quad 0 &{}\quad h_{6} &{}\quad 0 &{}\quad 0 &{}\quad h_{7} \\ 0 &{}\quad h_{6} &{}\quad h_{6} &{}\quad 0 &{}\quad h_{6} &{}\quad 0 &{}\quad 0 &{}\quad h_{7} \\ h_{5} &{}\quad 0 &{}\quad 0 &{}\quad h_{8} &{}\quad 0 &{}\quad h_{8} &{}\quad h_{8} &{}\quad 0 \\ 0 &{}\quad h_{6} &{}\quad h_{6} &{}\quad 0 &{}\quad h_{6} &{}\quad 0 &{}\quad 0 &{}\quad h_{7} \\ h_{5} &{}\quad 0 &{}\quad 0 &{}\quad h_{8} &{}\quad 0 &{}\quad h_{8} &{}\quad h_{8} &{}\quad 0 \\ h_{5} &{}\quad 0 &{}\quad 0 &{}\quad h_{8} &{}\quad 0 &{}\quad h_{8} &{}\quad h_{8} &{}\quad 0 \\ 0 &{}\quad h_{7} &{}\quad h_{7} &{}\quad 0 &{}\quad h_{7} &{}\quad 0 &{}\quad 0 &{}\quad h_{9} \end{array} \right] . \end{aligned}$$
(33)

Where

$$\begin{aligned} h_{1}=&\frac{1}{16}(5+3 e^{-8 \beta }),&h_{2}=&\frac{1}{16}t(-1+e^{-8 \beta }),\\ h_{3}=&\frac{1}{16}(1-e^{-8 \beta }),&h_{4}=&\frac{1}{32} e^{-18 \beta }(-3-6 e^{10 \beta }+3 e^{16 \beta }+6 e^{18 \beta },\\ h_{5}=&\frac{1}{32} e^{-18 \beta } (-3-2 e^{10 \beta }+3 e^{16 \beta }+2 e^{18 \beta }),&h_{6}=&\frac{1}{96} (10+9 e^{-18 \beta }+6 e^{-8 \beta }+7 e^{-2 \beta }),\\ h_{7}=&\frac{1}{32} e^{-18 \beta }(3-2 e^{10 \beta }-3 e^{16 \beta }+2 e^{18 \beta }),&h_{8}=&\frac{1}{96}(10-9 e^{-18 \beta }+6 e^{-8 \beta }-7 e^{-2 \beta }),\\ h_{9}=&\frac{1}{32} e^{-18 \beta }(3-6 e^{10 \beta }-3 e^{16 \beta }+6 e^{18 \beta }). \end{aligned}$$

1.2 Appendix 2. The case of mixed environment setup

By using Eq. (9) for mes, the average of the final density matrix for \(\mathcal {X}_{G}\) state in Eq. (3) is taken over the noise phase and we get;

$$\begin{aligned} \rho _{mes}^{\mathcal {X}_G}(\varphi _1,\varphi _2, \tau )=\left[ \begin{array}{cccccccc} h_{10} &{}\quad 0 &{}\quad h_{11} &{}\quad 0 &{}\quad 0 &{}\quad h_{11} &{}\quad 0 &{}\quad h_{10} \\ 0 &{}\quad h_{12} &{}\quad 0 &{}\quad h_{12} &{}\quad h_{12} &{}\quad 0 &{}\quad h_{12} &{}\quad 0 \\ h_{11} &{}\quad 0 &{}\quad h_{13} &{}\quad 0 &{}\quad 0 &{}\quad h_{13} &{}\quad 0 &{}\quad h_{11} \\ 0 &{}\quad h_{12} &{}\quad 0 &{}\quad h_{12} &{}\quad h_{12} &{}\quad 0 &{}\quad h_{12} &{}\quad 0 \\ 0 &{}\quad h_{12} &{}\quad 0 &{}\quad h_{12} &{}\quad h_{12} &{}\quad 0 &{}\quad h_{12} &{}\quad 0 \\ h_{11} &{}\quad 0 &{}\quad h_{13} &{}\quad 0 &{}\quad 0 &{}\quad h_{13} &{}\quad 0 &{}\quad h_{11} \\ 0 &{}\quad h_{12} &{}\quad 0 &{}\quad h_{12} &{}\quad h_{12} &{}\quad 0 &{}\quad h_{12} &{}\quad 0 \\ h_{10} &{}\quad 0 &{}\quad h_{11} &{}\quad 0 &{}\quad 0 &{}\quad h_{11} &{}\quad 0 &{}\quad h_{10} \end{array} \right] . \end{aligned}$$
(34)

By utilizing the final density matrix Eq. (9) for the \(\mathcal {X}_{W}\) state in mes situation, we obtain:

$$\begin{aligned} \rho _{mes}^{\mathcal {X}_W}(\varphi _1,\varphi _2, \tau )=\left[ \begin{array}{cccccccc} 0 &{}\quad 0 &{}\quad 0 &{}\quad h_{14} &{}\quad 0 &{}\quad 0 &{}\quad h_{14} &{}\quad 0 \\ 0 &{}\quad h_{15} &{}\quad h_{16} &{}\quad 0 &{}\quad h_{15} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad h_{16} &{}\quad h_{17} &{}\quad 0 &{}\quad h_{16} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ h_{14} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad h_{18} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad h_{15} &{}\quad h_{16} &{}\quad 0 &{}\quad h_{15} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad h_{18} &{}\quad 0 &{}\quad 0 &{}\quad h_{18} &{}\quad 0 \\ h_{14} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad h_{18} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array} \right] \end{aligned}$$
(35)

where

$$\begin{aligned} h_{10}=&\frac{1}{16} e^{-4 \beta } (4+e^{2 \beta }+3 e^{4 \beta }),&h_{11}=&\frac{1}{16} (-1+e^{-2 \beta }),\\ h_{12}=&-h_{11},&h_{13}=&\frac{1}{16} e^{-4 \beta } (-4+e^{2 \beta }+3 e^{4 \beta }),\\ h_{14}=&\frac{1}{12} e^{-10 \beta } (-1-e^{6 \beta }+e^{8 \beta }+e^{10 \beta }),&h_{15}=&\frac{e^{-5 \beta }}{3},\\ h_{16}=&\frac{1}{12} e^{-10 \beta } (1+e^{6 \beta }+e^{8 \beta }+e^{10 \beta }),&h_{17}=&\frac{e^{-3 \beta }}{3},\\ h_{18}=&\frac{1}{12} e^{-10 \beta } (-1+e^{6 \beta }-e^{8 \beta }+e^{10 \beta }). \end{aligned}$$

1.3 Appendix 3. The case of independent environment setup

Here, the final matrix for ies scheme is obtained from Eq. (10) by taking the average of the time-evolved density matrix for \(\mathcal {X}_{G}\) state given in Eq. (3) over the \(\mathcal {G_N}\) noise phase from Eq. (7). We followed it as:

$$\begin{aligned} \rho _{ies}^{\mathcal {X}_G}(\varphi _1,\varphi _2,\varphi _3, \tau )=\left[ \begin{array}{cccccccc} h_{19} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad h_{19} \\ 0 &{}\quad h_{20} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad h_{20} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad h_{20} &{}\quad 0 &{}\quad 0 &{}\quad h_{20} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad h_{20} &{}\quad h_{20} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad h_{20} &{}\quad h_{20} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad h_{20} &{}\quad 0 &{}\quad 0 &{}\quad h_{20} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad h_{20} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad h_{20} &{}\quad 0 \\ h_{19} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad h_{19} \end{array} \right] . \end{aligned}$$
(36)

For \(\mathcal {X}_{W}\) state, we use the density matrix given in Eq. (10) for the ies model and we get:

$$\begin{aligned} \rho _{ies}^{\mathcal {X}_W}(\varphi _1,\varphi _2,\varphi _3, \tau )=\left[ \begin{array}{cccccccc} h_{21} &{}\quad 0 &{}\quad 0 &{}\quad h_{22} &{}\quad 0 &{}\quad h_{22} &{}\quad h_{22} &{}\quad 0 \\ 0 &{}\quad h_{23} &{}\quad h_{24} &{}\quad 0 &{}\quad h_{24} &{}\quad 0 &{}\quad 0 &{}\quad h_{25} \\ 0 &{}\quad h_{24} &{}\quad h_{23} &{}\quad 0 &{}\quad h_{24} &{}\quad 0 &{}\quad 0 &{}\quad h_{25} \\ h_{22} &{}\quad 0 &{}\quad 0 &{}\quad h_{26} &{}\quad 0 &{}\quad h_{27} &{}\quad h_{27} &{}\quad 0 \\ 0 &{}\quad h_{24} &{}\quad h_{24} &{}\quad 0 &{}\quad h_{23} &{}\quad 0 &{}\quad 0 &{}\quad h_{25} \\ h_{22} &{}\quad 0 &{}\quad 0 &{}\quad h_{27} &{}\quad 0 &{}\quad h_{26} &{}\quad h_{27} &{}\quad 0 \\ h_{22} &{}\quad 0 &{}\quad 0 &{}\quad h_{27} &{}\quad 0 &{}\quad h_{27} &{}\quad h_{26} &{}\quad 0 \\ 0 &{}\quad h_{25} &{}\quad h_{25} &{}\quad 0 &{}\quad h_{25} &{}\quad 0 &{}\quad 0 &{}\quad h_{28} \end{array} \right] . \end{aligned}$$
(37)

Where

$$\begin{aligned} h_{19}=&\frac{1}{8}+\frac{3 e^{-4 \beta }}{8},&h_{20}=&\frac{1}{8}-\frac{e^{-4 \beta }}{8},\\ h_{21}=&\frac{1}{8} e^{-6 \beta } (-1+e^{2 \beta }) (1+e^{2 \beta })^2,&h_{22}=&\frac{1}{12} e^{-6 \beta } (-1+e^{2 \beta }) (1+e^{2 \beta })^2,\\\ h_{23}=&\frac{1}{24} e^{-6 \beta } (3+e^{2 \beta }+e^{4 \beta }+3 e^{6 \beta }),&h_{24}=&\frac{1}{12} e^{-6 \beta } (1+e^{2 \beta }+e^{4 \beta }+e^{6 \beta }),\\ h_{25}=&\frac{1}{12} e^{-6 \beta } (-1+e^{2 \beta })^2 (1+e^{2 \beta }),&h_{26}=&\frac{1}{24} e^{-6 \beta } (-3+e^{2 \beta }-e^{4 \beta }+3 e^{6 \beta }),\\ h_{27}=&\frac{1}{12} e^{-6 \beta } (-1+e^{2 \beta }-e^{4 \beta }+e^{6 \beta }),&h_{28}=&\frac{1}{8} e^{-6 \beta } (-1+e^{2 \beta })^2 (1+e^{2 \beta }). \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rahman, A.U., Noman, M., Javed, M. et al. Quantum correlations of tripartite entangled states under Gaussian noise. Quantum Inf Process 20, 290 (2021). https://doi.org/10.1007/s11128-021-03231-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-021-03231-9

Keywords

Search

Navigation