Skip to main content

Advertisement

Springer Nature Link
Log in

Entanglement and nonlocality dynamics of a Bell state and the GHZ state in a noisy environment

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

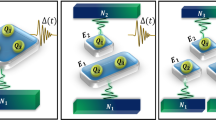
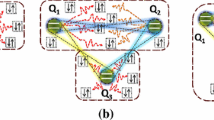
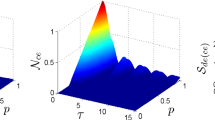
We investigate the entanglement and nonlocality dynamics of a two-qubit Bell state and the three-qubit Greenberger–Home–Zeilinger (GHZ) state in a noisy environment by solving analytically a master equation in the Lindblad form. In the case of the Bell state, we obtain the analytic expressions of the concurrence and the maximal violation of the Clauser–Horne–Shimony–Holt inequality of the evolution state. In the case of the three-qubit GHZ state, we obtain the analytic formula of the genuinely multipartite concurrence of the evolution state. Usually, it is difficult to give the analytic expression of the maximum violation of the Svetlichny inequality for a general three-qubit state, but we find the analytic expression for a class of three-qubit states whose correlation matrices are of a special form. We use this result to obtain the analytic expression of the maximum violation of the Svetlichny inequality of the evolution state when parameters in the master equation meet certain conditions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Horodecki, R., Horodecki, P., Horodecki, M., et al.: Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  2. Buhrman, H., Cleve, R., Massar, S., et al.: Non-locality and communication complexity. Rev. Mod. Phys. 82(1), 665–698 (2009)

    Article  ADS  Google Scholar 

  3. Bardyn, C.E., Liew, T., Massar, S., et al.: Device-independent state estimation based on Bell’s inequalities. Phys. Rev. A 80(6), 062327 (2009)

    Article  ADS  Google Scholar 

  4. Werner, R.F.: Quantum states with Einstein–Podolsky–Rosen correlations admitting a hidden-variable model. Phys. Rev. A 40(8), 4277–4281 (1989)

    Article  ADS  Google Scholar 

  5. Brunner, N., Cavalcanti, D., Pironio, S., et al.: Bell nonlocality. Rev. Mod. Phys. 86(2), 419–478 (2014)

    Article  ADS  Google Scholar 

  6. Gühne, O., Toth, G.: Entanglement detection. Phys. Rep. 474(1–6), 1–75 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  7. Harshman, N.L., Flynn, W.F.: Entanglement in massive coupled oscillators. Quantum Inf. Comput. 11(3), 278–299 (2010)

    MathSciNet  MATH  Google Scholar 

  8. Yu, T., Eberly, J.H.: Finite-time disentanglement via spontaneous emission. Phys. Rev. Lett. 93(14), 140404 (2004)

    Article  ADS  Google Scholar 

  9. Lopez, C.E., Romero, G., Lastra, F., et al.: Sudden Birth versus sudden death of entanglement in multipartite systems. Phys. Rev. Lett. 101(8), 080503 (2008)

    Article  ADS  Google Scholar 

  10. Yang, Q., Yang, M., Cao, Z.L.: Cavity-loss-induced Bell-nonlocality sudden death in the Tavis–Cummings model. Phys. Lett. A 372(46), 6843–6846 (2008)

    Article  ADS  Google Scholar 

  11. Batle, J.: Nonlocality and entanglement in the XY model. Phys. Rev. A 82(6), 2212–2215 (2010)

    Article  MathSciNet  Google Scholar 

  12. Zhen, X.L., Yang, Q., Yang, M., et al.: Bell-nonlocality dynamics of three remote atoms in Tavis–Cummings and Jaynes–Cummings models. Commun. Theor. Phys. 62, 795 (2014)

    Article  ADS  MathSciNet  Google Scholar 

  13. Aolita, L., Melo, F.D., Davidovich, L.: Open-system dynamics of entanglement: a key issues review. Rep. Prog. Phys. 78(4), 042001 (2015)

    Article  ADS  Google Scholar 

  14. Jaeger, G., Ann, K.: Local basis-dependent noise-induced Bell-nonlocality sudden death in tripartite systems. Phys. Rev. A 372(13), 2212–2216 (2008)

    MathSciNet  MATH  Google Scholar 

  15. Qiu, L.: Nonlocality sudden birth and transfer in system and environment. Chin. Phys. Lett. 28(3), 030301 (2011)

    Article  ADS  Google Scholar 

  16. Lendi, K.: Selected aspects of Markovian and non-Markovian quantum master equations. Lect. Notes Phys. 622, 31–46 (2003)

    Article  ADS  Google Scholar 

  17. Laskowski, W., Paterek, T., Brukner, C., et al.: Entanglement and communication-reducing properties of noisy N-qubit states. Phys. Rev. A 81(4), 042101 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  18. Chaves, R., Cavalcanti, D., Aolita, L., et al.: Multipartite quantum nonlocality under local decoherence. Phys. Rev. A 86(1), 17258–17270 (2012)

    Article  Google Scholar 

  19. Oh, S., Lee, S., Lee, H.W.: Fidelity of quantum teleportation through noisy channels. Phys. Rev. A 66(2), 022316 (2002)

    Article  ADS  MathSciNet  Google Scholar 

  20. Jung, E., Hwang, M.R., Ju, Y.H., et al.: Greenberger–Horne–Zeilinger versus W states: quantum teleportation through noisy channels. Phys. Rev. A 78, 012312 (2008)

    Article  ADS  Google Scholar 

  21. Su, Z., Li, L., Ling, J.: An approach for quantitatively analyzing the genuine tripartite nonlocality of general three-qubit states. Quantum Inf. Process. 17(4), 85 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  22. Plenio, M.B., Virmani, S.: An introduction to entanglement measures. Quantum Inf. Comput. 7(1), 1–51 (2005)

    MathSciNet  MATH  Google Scholar 

  23. Wootters, W.K.: Entanglement of formation of an arbitrary state of two qubits. Found. Phys. Lett. 14(10), 199–212 (1997)

    Google Scholar 

  24. Ma, Z.H., Chen, Z.H., Chen, J.L., et al.: Measure of genuine multipartite entanglement with computable lower bounds. Phys. Rev. A 83(6), 35–40 (2011)

    Google Scholar 

  25. Mazzola, L., Bellomo, B., Franco, R.L., et al.: Connection among entanglement, mixedness and nonlocality in a dynamical context. Phys. Rev. A 81(81), 052116 (2010)

    Article  ADS  Google Scholar 

  26. Wang, K., Zheng, Z.J.: Violation of Svetlichny inequality in triple Jaynes–Cummings models. Sci. Rep. 10(1), 1–10 (2020)

    Article  Google Scholar 

  27. Rafsanjani, S., Huber, M., Broadbent, C.J., et al.: Genuinely multipartite concurrence of N-qubit X-matrices. Phys. Rev. A 86(6), 11987–11987 (2012)

    Google Scholar 

  28. Horodecki, R., Horodecki, P., Horodecki, M.: Violating Bell inequality by mixed spin-12 states: necessary and sufficient condition. Phys. Lett. A 200(5), 340–344 (1995)

    Article  ADS  MathSciNet  Google Scholar 

  29. Svetlichny, G.: Distinguishing three-body from two-body nonseparability by a Bell-type inequality. Phys. Rev. D 35(10), 3066–3069 (1987)

    Article  ADS  MathSciNet  Google Scholar 

  30. Derkacz, L., Lech, J.: Clauser–Horne–Shimony–Holt violation and the entropy-concurrence plane. Phys. Rev. A 72(4), 42321 (2005)

    Article  ADS  MathSciNet  Google Scholar 

  31. Ghose, S., Sinclair, N., Debnath, S., et al.: Tripartite entanglement versus tripartite nonlocality in three-qubit Greenberger–Horne–Zeilinger-class states. Phys. Rev. Lett. 102(25), 250404 (2009)

    Article  ADS  Google Scholar 

  32. Paul, B., Mukherjee, K., Sarkar, D.: Nonlocality of three-qubit Greenberger–Horne–Zeilinger-symmetric states. Phys. Rev. A 94(3), 032101 (2016)

    Article  ADS  Google Scholar 

  33. Lindblad, G.: On the generators of quantum dynamical semigroups. Commun. Math. Phys. 48(2), 119–130 (1976)

    Article  ADS  MathSciNet  Google Scholar 

  34. Alicki, R.: General theory and applications to unstable particles. Lect. Notes Phys. 717, 1–46 (2007)

    Article  ADS  Google Scholar 

  35. Singh, H., Dorai, K.: Evolution of tripartite entangled states in a decohering environment and their experimental protection using dynamical decoupling. Phys. Rev. A 97, 022302 (2018)

    Article  ADS  Google Scholar 

  36. Men, Q.T., Jiang, L.Z.: Separability of evolving W state in a noise environment. Commun. Theor. Phys. 73(4), 045101 (2021)

    Article  ADS  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work is supported by Key Research and Development Project of Guang dong Province under Grant No. 2020B0303300001 and the Guangdong Basic and Applied Basic Research Foundation under Grant No. 2020B1515310016. We appreciate Chang-Yue Zhang for her useful discussion.

Author information

Authors and Affiliations

  1. Department of Mathematics, South China University of Technology, Guangzhou, 510641, People’s Republic of China

    Yue-Qiu Chen, Hao Shu & Zhu-Jun Zheng

  2. Laboratory of Quantum Science and Engineering, South China University of Technology, Guangzhou, 510641, People’s Republic of China

    Yue-Qiu Chen, Hao Shu & Zhu-Jun Zheng

Authors
  1. Yue-Qiu Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Hao Shu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Zhu-Jun Zheng
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Zhu-Jun Zheng.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, YQ., Shu, H. & Zheng, ZJ. Entanglement and nonlocality dynamics of a Bell state and the GHZ state in a noisy environment. Quantum Inf Process 20, 323 (2021). https://doi.org/10.1007/s11128-021-03263-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-021-03263-1

Keywords