Skip to main content
Springer Nature Link
Log in

The measurement-induced nonlocality of two spins in a single-model cavity system

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

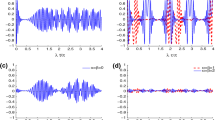
We investigate the dynamics of measurement-induced nonlocality (MIN) with two spins in an ideal single-mode optical cavity. The two-spin entangled states are generated firstly under the photon coherent state assumption by means of the variational method. The time evolution of MIN is then examined based on the derived analytical expressions of the reduced density operator of two spins. It is shown that MIN remains in its upper bound all the time and independent of the average photon number of the coherent field when the two spins are initially in the singlet state, which just is the eigenstate of our model. However, for the initial general two-spin entangled states of antiparallel and parallel spin polarizations, MIN strongly depends on the average photon number and initial angle parameters. We provide a detailed analysis of MIN dynamics by the numerical calculation, and reveal some significant results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Eisert, J., Cramer, M., Plenio, M.B.: Colloquium: area laws for the entanglement entropy. Rev. Mod. Phys. 82, 277 (2010)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  2. De Chiara, G., Sanpera, A.: Genuine quantum correlations in quantum many-body systems: a review of recent progress. Rep. Prog. Phys. 81, 074002 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  3. Gour, G., Scandolo, C.M.: Dynamical entanglement. Phys. Rev. Lett. 125, 180505 (2020)

    Article  ADS  MathSciNet  Google Scholar 

  4. Paneru, D., Cohen, E., Fickler, R., Boyd, R.W., Karimi, E.: Entanglement: Quantum or classical? Rep. Prog. Phys. 83, 064011 (2020)

    Article  ADS  MathSciNet  Google Scholar 

  5. Dan, K., Mor, T., Ratsaby, G.: Quantum advantage without entanglement. Quantum Inf. Comput. 6, 606–615 (2012)

    MathSciNet  MATH  Google Scholar 

  6. Ollivier, H., Zurek, W.H.: Quantum discord: a measure of the quantumness of correlations. Phys. Rev. Lett. 88, 017901 (2001)

    Article  ADS  MATH  Google Scholar 

  7. Ali, M., Rau, A.R.P., Alber, G.: Quantum discord for two-qubit X-states. Phys. Rev. A 81, 042105 (2010)

    Article  ADS  Google Scholar 

  8. Li, B., Wang, Z.X., Fei, S.M.: Quantum discord and geometry for a class of two-qubit states. Phys. Rev. A 83, 1293–1304 (2011)

    Google Scholar 

  9. Modi, K., Brodutch, A., Cable, H., Paterek, T., Vedral, V.: The classical-quantum boundary for correlations: discord and related measures. Rev. Mod. Phys. 84, 1655–1707 (2012)

    Article  ADS  Google Scholar 

  10. Hu, M.L., Hu, X., Wang, J., Peng, Y., Zhang, Y.R., Fan, H.: Quantum coherence and geometric quantum discord. Phys. Rep. 762, 1 (2018)

    ADS  MathSciNet  MATH  Google Scholar 

  11. Radhakrishnan, C., Laurière, M., Byrnes, T.: Multipartite generalization of quantum discord. Phys. Rev. Lett. 124, 110401 (2020)

    Article  ADS  MathSciNet  Google Scholar 

  12. Luo, S.: Using measurement-induced disturbance to characterize correlations as classical or quantum. Phys. Rev. A 77, 681–700 (2008)

    Article  Google Scholar 

  13. Rulli, C.C., Sarandy, M.S.: Global quantum discord in multipartite systems. Phys. Rev. A 84, 5388–5393 (2011)

    Article  Google Scholar 

  14. Paula, F.M., Oliveira, T.R.D., Sarandy, M.S.: Geometric quantum discord through the Schatten 1-norm. Phys. Rev. A 87, 4996–4996 (2013)

    Article  Google Scholar 

  15. Dakić, B., Vedral, V., Brukner, Č: Necessary and sufficient condition for nonzero quantum discord. Phys. Rev. Lett. 105, 190502.1-190502.4 (2010)

    Article  ADS  MATH  Google Scholar 

  16. Luo, S., Fu, S.: Measurement-induced nonlocality. Phys. Rev. Lett. 106, 120401 (2011)

    Article  ADS  MATH  Google Scholar 

  17. Girolami, D., Tufarelli, T., Adesso, G.: Characterizing nonclassical correlations via local quantum uncertainty. Phys. Rev. Lett. 110, 240402 (2013)

    Article  ADS  Google Scholar 

  18. Hu, M.L., Fan, H.: Measurement-induced nonlocality based on the trace norm. New J. Phys. 17, 33004–33012 (2015)

    Article  Google Scholar 

  19. Zhang, L.Q., Ma, T.T., Yu, C.S.: Measurement-induced nonlocality in arbitrary dimensions in terms of the inverse approximate joint diagonalization. Phys. Rev. A 97, 032112 (2018)

    Article  ADS  Google Scholar 

  20. Muthuganesan, R., Sankaranarayanan, R.: Fidelity based measurement induced nonlocality. Phys. Lett. A 381, 3028 (2017)

    Article  ADS  MATH  Google Scholar 

  21. Datta, A., Shaji, A., Caves, C.M.: Quantum discord and the power of one qubit. Phys. Rev. Lett. 100, 050502 (2008)

    Article  ADS  Google Scholar 

  22. Piani, M., Horodecki, P., Horodecki, R.: No-local-broadcasting theorem for multipartite quantum correlations. Phys. Rev. Lett. 100, 090502 (2008)

    Article  ADS  Google Scholar 

  23. Dakić, B., Lipp, Y.O., et al.: Quantum discord as resource for remote state preparation. Nat. Phys. 8, 666–670 (2012)

    Article  Google Scholar 

  24. Brodutch, A., Terno, D.R.: Quantum discord, local operations, and Maxwell’s demons. Phys. Rev. A 81, 062103 (2010)

  25. Kon, W.Y., Krisnanda, T., Sengupta, P., Paterek, T.: Nonclassicality of spin structures in condensed matter: an analysis of Sr\( _{14}\)Cu\(_{24}\)O\(_{41}\). Phys. Rev. B 100, 235103 (2019)

    Article  ADS  Google Scholar 

  26. Korolkova, N., Leuchs, G.: Quantum correlations in separable multi-mode states and in classically entangled light. Rep. Prog. Phys. 82, 056001 (2019)

    Article  ADS  MathSciNet  Google Scholar 

  27. Liang, J., Zhang, C.: Geometric quantum discord of Heisenberg model with dissipative terms. Sci. Rep. 10, 10817 (2020)

    Article  ADS  Google Scholar 

  28. Katiyar, H., Roy, S.S., Mahesh, T.S.: Evolution of quantum discord and its stability in two-qubit NMR systems. Phys. Rev. A 86, 012309 (2012)

    Article  ADS  Google Scholar 

  29. Micadei, K., Peterson, J.P.S., et al.: Reversing the direction of heat flow using quantum correlations. Nat. Commun. 10, 2456 (2019)

    Article  ADS  Google Scholar 

  30. Cao, W., Lu, X., Meng, X., Sun, J., Shen, H., Xiao, Y.: Reservoir-mediated quantum correlations in non-Hermitian optical system. Phys. Rev. Lett. 124, 030401 (2020)

    Article  ADS  Google Scholar 

  31. Sales, J.S., Cardoso, W.B., Avelar, A.T., De Almeida, N.G.: Dynamics of nonclassical correlations via local quantum uncertainty for atom and field interacting into a lossy cavity QED. Physica A 443, 399–405 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  32. Zhang, G.F., Fan, H., Ji, A.L., Jiang, Z.T., Abliz, A., Liu, W.M.: Quantum correlations in spin models. Ann. Phys. 326, 2694 (2011)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  33. Zhang, G.F., Jiang, Z.T., Abliz, A.: Measurement-induced disturbance and thermal entanglement in spin models. Ann. Phys. 326, 867–875 (2011)

    Article  ADS  MATH  Google Scholar 

  34. Zhang, G.F., Fan, H., Ji, A.L., Liu, W.M.: Dynamics of geometric discord and measurement-induced nonlocality at finite temperature. Eur. Phys. J. D 66, 34 (2012)

    Article  ADS  Google Scholar 

  35. Ramzan, M.: Decoherence dynamics of geometric measure of quantum discord and measurement induced nonlocality for noninertial observers at finite temperature. Quantum Inf. Process. 12, 2721 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  36. Hu, M.L., Lian, H.L.: Geometric quantum discord and non-Markovianity of structured reservoirs. Ann. Phys. 362, 795 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  37. Li, J.Q., Cui, X.L., Liang, J.Q.: The dynamics of quantum correlation with two controlled qubits under classical dephasing environment. Ann. Phys. 354, 365 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  38. Bai, X.M., Wang, N., Li, J.Q., Liang, J.Q.: The creation of quantum correlation and entropic uncertainty relation in photonic crystals. Quantum Inf. Process. 15, 2771 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  39. Orthey, A.C., Jr., Angelo, R.M.: Nonlocality, quantum correlations, and violations of classical realism in the dynamics of two noninteracting quantum walkers. Phys. Rev. A 100, 042110 (2019)

    Article  ADS  Google Scholar 

  40. Ban, M.: Decoherence of a two-qubit system interacting with initially correlated random telegraph noises. Quantum Inf. Process. 19, 1–18 (2020)

    Article  ADS  MathSciNet  Google Scholar 

  41. Pourkarimi, M.R., Haddadi, S.: Quantum-memory-assisted entropic uncertainty, teleportation, and quantum discord under decohering environments. Laser Phys. Lett. 17, 025206 (2020)

    Article  ADS  Google Scholar 

  42. Vimal, V.K., Subrahmanyam, V.: Magnetization revivals and dynamics of quantum correlations in a Kitaev spin chain. Phys. Rev. A 102, 012406 (2020)

    Article  ADS  MathSciNet  Google Scholar 

  43. Li, X.X., Yin, H.D., Li, D.X., Shao, X.Q.: Deterministic generation of maximally discordant mixed states by dissipation. Phys. Rev. A 101, 012329 (2020)

    Article  ADS  Google Scholar 

  44. Berrada, K., Raffah, B., Eleuchd, H.: Quantum correlations and coherence in a driven two-qubit system under non-Markovian dissipative effect. Results Phys. 17, 103083 (2020)

    Article  Google Scholar 

  45. Hu, M.L., Fan, H.: Dynamics of entropic measurement-induced nonlocality in structured reservoirs. Ann. Phys. 327, 2343–2353 (2012)

    Article  ADS  MATH  Google Scholar 

  46. Wang, L.D., Wang, L.T., Yang, M., Xu, J.Z., Wang, Z.D., Bai, Y.K.: Entanglement and measurement-induced nonlocality of mixed maximally entangled states in multipartite dynamics. Phys. Rev. A 93, 062309 (2016)

    Article  ADS  Google Scholar 

  47. Zhang, G.F., Ji, A.L., Fan, H., Liu, W.M.: Quantum correlation dynamics of two qubits in noisy environments: the factorization law and beyond. Ann. Phys. 327, 2074–2084 (2012)

    Article  ADS  MATH  Google Scholar 

  48. Mohamed, A.B.A.: Non-local correlation and quantum discord in two atoms in the non-degenerate model. Ann. Phys. 327, 3130–3137 (2012)

    Article  ADS  MATH  Google Scholar 

  49. Mohamed, A.B.A., Joshi, A., Hassane, S.S.: Enhancing non-local correlations in the bipartite partitions of two qubit-system with non-mutual interaction. Ann. Phys. 366, 32–44 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  50. Mohamed, A.B.A., Hashem, M.: The behavior of the generated quantum correlations in two-SC-qubit system strongly coupled with a SC cavity in the presence of local noise. Quantum Inf. Process. 17, 217 (2018)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  51. Mohamed, A.B.A., Metwally, N.: Enhancing non-local correlations in a dissipative two-qubit system via dipole-dipole interplay. Quantum Inf. Process. 18, 79 (2019)

    Article  ADS  MATH  Google Scholar 

  52. Mohamed, A.B.A., Eleuch, H., Ooi, C.H.R.: Non-locality correlation in two driven qubits inside an open coherent cavity: trace norm distance and maximum Bell function. Sci. Rep. 9, 19632 (2019)

    Article  ADS  Google Scholar 

  53. Mohamed, A.B.A., Hessian, H.A., Eleuch, H.: Quantum correlations of two qubits beyond entanglement in two lossy cavities linked by a waveguide. Chaos Soliton Fract. 135, 109773 (2020)

    Article  MathSciNet  Google Scholar 

  54. Huang, Z., Zhang, C.: Protecting quantum correlation from correlated amplitude damping channel. Braz. J. Phys. 47, 400 (2017)

    Article  ADS  Google Scholar 

  55. Ma, Y.X., Li, L., Hou, X.W.: Quantum nonlocality in the spin-s Heisenberg models with the Dzyaloshinskii–Moriya interaction. Quantum Inf. Process. 18, 288 (2019)

    Article  ADS  MathSciNet  Google Scholar 

  56. Hensen, B., Kalb, N., et al.: Loophole-free Bell test using electron spins in diamond: second experiment and additional analysis. Sci. Rep. 6, 30289 (2016)

    Article  ADS  Google Scholar 

  57. Kim, M.S., Lee, J., Ahn, D., Knight, P.L.: Entanglement induced by a single-mode heat environment. Phys. Rev. A 65, 579–579 (2002)

    Article  Google Scholar 

  58. Zhao, X.Q., Liu, N., Liang, J.Q.: Nonlinear atom–photon-interaction-induced population inversion and inverted quantum phase transition of Bose–Einstein condensate in an optical cavity. Phys. Rev. A 90, 023622 (2014)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11105087,11772177,12047571), and the Science and Technological Innovation Programs of Higher Education institutions in Shanxi Province (STIP) (Grant Nos. 2019L0069, 2020L0586, 2020L0607).

Author information

Authors and Affiliations

  1. Institute of Theoretical Physics, State Key Laboratory of Quantum Optics and Quantum Optics Devices, Shanxi University, Taiyuan, 030006, Shanxi, China

    Xue-Yun Bai, Ni Liu, Jun-Qi Li & J.-Q. Liang

  2. School of Mathematics, Jinzhong University, Jinzhong, 030619, Shanxi, China

    Xue-Min Bai

Authors
  1. Xue-Yun Bai
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xue-Min Bai
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Ni Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Jun-Qi Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. J.-Q. Liang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jun-Qi Li.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bai, XY., Bai, XM., Liu, N. et al. The measurement-induced nonlocality of two spins in a single-model cavity system. Quantum Inf Process 20, 364 (2021). https://doi.org/10.1007/s11128-021-03315-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-021-03315-6

Keywords