Entanglement measures of a pentapartite W-class state in the noninertial frame

Abstract

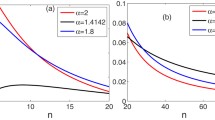
We study the entanglement of a pentapartite W-class state system in the noninertial frame when transformed from the Minkowski coordinates to Rindler space. Five different cases are considered, one of which includes one to five of 5 qubits selected arbitrarily. The selected qubits move at an acceleration a, but the others remain stationary. The negativities of 1–1 tangle, 1–4 tangle and von Neumann entropy which are used to describe the nature of entanglement are systematically carried out. We discover that the negativities of all 1–1 and 1–4 tangles and whole entanglement measures, which include $\pi _{5}$ and $\Pi _5$, decrease as the acceleration parameter r increases. We notice that entanglements of both $\pi _{5}$ and $\Pi _5$ still exist even if the acceleration parameter r tends to infinity except for a special case where all five observers are accelerated simultaneously. This implies that the degree of entanglement in this particular case is minimal. However, it is shown from the plot of 1–1 tangle that entanglement will disappear at $r>0.61548$ when one of two observers is accelerated, but it will vanish at $r>0.38071$ when both observers are accelerated. We also note that compared with the other four cases, the entanglement is more robust when one of five qubits is accelerated. In the case of four or five qubits being accelerated, the difference between the algebraic average $\pi _{5}$ and geometric average $\Pi _5$ is almost equal to zero, but their difference gradually increases as the number of accelerated observer decreases. We also study the von Neumann entropy of pentapartite system, the tetrapartite, tripartite and bipartite subsystems. We find that all of them increase in general trend with the increasing acceleration parameter r except for a special case, when there is on accelerated observer. However, the von Neumann entropies of the subsystems $S_{\alpha \beta \gamma \delta }$, $S_{\alpha \beta \gamma }$ and $S_{\alpha \beta }$ increase when all observers are accelerated simultaneously and then decrease as the acceleration parameter r increases. In special cases, that is, without any accelerated observers, the von Neumann entropies of these subsystems are constants, say 0.721928, 0.970951 and 0.970951, respectively. These results once again confirm that the degree of entanglement degrades due to the Unruh effect. The present results are also compared with those of tripartite and tetrapartite W-class cases.

Appendix A: Symmetry property of the negativity

In this appendix, for convenience we list some useful relations about the 1–4 tangle and 1–1 tangle as follows:

• 1. 1–4 tangle: $N_{A(BCDE_{I})} = N_{B(ACDE_{I})} = N_{C(ABDE_{I})} = N_{D(ABCE_{I})}$, $N_{A(BCD_{I}E_{I})} = N_{B(ACD_{I}E_{I})} = N_{C(ABD_{I}E_{I})}$, $N_{D_{I}(ABCE_{I})}=N_{E_{I}(ABCD_{I})}$, $N_{A(BC_{I}D_{I}E_{I})} = N_{B(AC_{I}D_{I}E_{I})}$, $N_{C_{I}(ABD_{I}E_{I})} = N_{D_{I}(ABC_{I}E_{I})}=N_{E_{I}(ABC_{I}D_{I})}$, $N_{B_{I}(AC_{I}D_{I}E_{I})} = N_{C_{I}(AB_{I}D_{I}E_{I})} = N_{D_{I}(AB_{I}C_{I}E_{I})}=N_{E_{I}(AB_{I}C_{I}D_{I})}$ and $N_{A_{I}(B_{I}C_{I}D_{I}E_{I})} = N_{B_{I}(A_{I}C_{I}D_{I}E_{I})} = N_{C_{I}(A_{I}B_{I}D_{I}E_{I})} = N_{D_{I}(A_{I}B_{I}C_{I}E_{I})}=N_{E_{I}(A_{I}B_{I}C_{I}D_{I})}$.

• 2. 1–1 tangle: $N_{A(B)} = N_{A(C)} = N_{B(C)} = N_{A(D)} = N_{B(D)} = N_{C(D)}$, $N_{A(BI)} = N_{A(CI)} = N_{B(CI)} = N_{A(DI)} = N_{B(DI)} = N_{C(DI)} = N_{A(EI)} = N_{B(EI)} = N_{C(EI)} = N_{D(EI)}$, $N_{AI(BI)} = N_{AI(CI)} = N_{BI(CI)} = N_{AI(DI)} = N_{BI(DI)} = N_{CI(DI)} = N_{AI(EI)} = N_{BI(EI)} = N_{CI(EI)} = N_{DI(EI)}$.