Skip to main content

Advertisement

Springer Nature Link
Log in

Target-generating quantum error correction coding scheme based on generative confrontation network

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

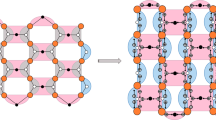
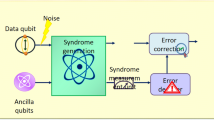
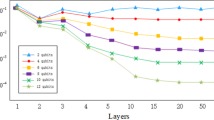
In order to solve the errors generated during the operation of quantum computers, quantum error correction codes are the most effective candidates at the moment. The best choice of error correction position and the improvement of decoding efficiency are problems that need to be solved urgently. This paper proposes a Grover search algorithm that targets regulatory topological codes, which can be applied to search the most likely error positions of surface code and color code with different code distances. Compared with the previous error qubit search, the error location determination time is shortened by 40\(\%\). According to the error probability of different qubits, the top 30\(\%\) of the qubits are selected for centralized error correction. We use the Generative Adversarial Network (GAN) in machine learning as the error correction training model. The training accuracy of the original neural network can only be improved from about 65\(\%\) to about 98\(\%\). Compared with the 69\(\%\) training accuracy of the minimum perfect matching (MWPM) algorithm, it has been greatly improved. At the same time, in order to speed up the efficiency of decoding and solve the problem of the correlation between surface code and color code vertices and the grid space, we chose a reinforcement learning decoder. Compared with local MWPM decoding, the error correction is only 56\(\%\), and it is difficult to achieve a large error-tolerant calculation under the threshold of about 4\(\%\), which makes the error correction success rate reach 94.5\(\%\) under the GAN training model, and it is better to correct the error. It is possible that the error code can be corrected at a low threshold of about 8.4\(\%\).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Fowler, A.G., Mariantoni, M., Martinis, J.M., Cleland, A.N.: Surface codes: towards practical large-scale quantum computation. Phys. Rev. A. 86, 032324 (2012)

    Article  ADS  Google Scholar 

  2. Nickerson, N.H., Li, Y., Benjamin, S.C.: Topological quantum computing with a very noisy network and local error rates approaching one percent. Nat. Commun. 4, 1–5 (2013)

    Article  Google Scholar 

  3. Zhou, N.R., Hua, T.X., Gong, L.H., Pei, D.J., Liao, Q.H.: Quantum image encryption based on generalized Arnold transform and double random-phase encoding. Quantum. Inf. Process. 14, 1193–1213 (2015)

    Article  MathSciNet  MATH  ADS  Google Scholar 

  4. Sarvepalli, P., Raussendorf, R.: Efficient decoding of topological color codes. Phys. Rev. A. 85, 022317 (2012)

    Article  ADS  Google Scholar 

  5. Leshno, M., Lin, V.Y., Pinkus, A., Schocken, S.: Multilayer feedforward networks with a nonpolynomial activation function can approximate any function. Neural Netw. 6, 861–867 (1993)

    Article  Google Scholar 

  6. Davaasuren, A., Suzuki, Y., Fujii, K., Koashi, M.: General framework for constructing fast and near-optimal machine-learning-based decoder of the topological stabilizer codes. Phys. Review. R. 2, 033399 (2020)

    Article  ADS  Google Scholar 

  7. Fowler, A.G.: Proof of finite surface code threshold for matching. Phys. Rev. Lett. 109, 180502 (2012)

    Article  ADS  Google Scholar 

  8. Andersen, C.K., Remm, A., Lazar, S., Krinner, S., Lacroix, N., Norris, G.J., Wallraff, A.: Repeated quantum error detection in a surface code. Nat. Phys. 16, 875–880 (2020)

    Article  Google Scholar 

  9. Yang, L., Liu, Y.C., Li, Y.S.: Quantum teleportation of particles in an environment. Chinese. Phys. B. 29, 060301 (2020)

    Article  ADS  Google Scholar 

  10. Deville, A., Deville, Y.: N-qubit system in a pure state: a necessary and sufficient condition for unentanglement. Quantum. Inf. Process. 18, 1–16 (2019)

    Article  MathSciNet  Google Scholar 

  11. Peng, T., Harrow, A.W., Ozols, M., Wu, X.: Simulating large quantum circuits on a small quantum computer. Phys. Rev. Lett. 125, 150504 (2020)

    Article  ADS  Google Scholar 

  12. Zhou, L., Sheng, Y.B., Long, G.L.: Device-independent quantum secure direct communication against collective attacks. Sci. Bull. 65, 12–20 (2020)

    Article  Google Scholar 

  13. Colomer, L.D., Skotiniotis, M., Muñoz-Tapia, R.: Reinforcement learning for optimal error correction of toric codes. Phys. Lett. A 384, 126353 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  14. Zhou, N.R., Xu, Q.D., Du, N.S., Gong, L.H.: Semi-quantum private comparison protocol of size relation with d-dimensional Bell states. Quantum. Inf. Process. 20, 1–15 (2021)

    Article  MathSciNet  Google Scholar 

  15. Zheng, L.N., Qi, L., Cheng, L.Y., Wang, H.F., Zhang, S.: Defect-induced controllable quantum state transfer via a topologically protected channel in a flux qubit chain. Phy. Rev. A. 102, 012606 (2020)

    Article  ADS  Google Scholar 

  16. Shao, C.: A quantum model of feed-forward neural networks with unitary learning algorithms. Quantum. Inf. Process. 19, 1–17 (2020)

    Article  MathSciNet  ADS  Google Scholar 

  17. Baireuther, P., O’Brien, T.E., Tarasinski, B., Beenakker, C.W.: Machine-learning-assisted correction of correlated qubit errors in a topological code. Quantum. 2, 48 (2018)

    Article  Google Scholar 

  18. Ataides, J.P.B., Tuckett, D.K., Bartlett, S.D., Flammia, S.T., Brown, B.J.: The XZZX surface code. Nat. Commun. 12, 1–12 (2021)

    Google Scholar 

  19. Horsman, C., Fowler, A.G., Devitt, S., Van Meter, R.: Surface code quantum computing by lattice surgery. New. J. Phys. 14, 123011 (2012)

    Article  MathSciNet  MATH  ADS  Google Scholar 

  20. Long, G.L., Li, X., Sun, Y.: Phase matching condition for quantum search with a generalized initial state. Phys. Lett. A. 294, 143–152 (2002)

    Article  MathSciNet  MATH  ADS  Google Scholar 

  21. Mussinger, M., Delgado, A., Alber, G.: Error avoiding quantum codes and dynamical stabilization of Grover’s algorithm. New. J. Phys. 2, 19 (2000)

    Article  MATH  ADS  Google Scholar 

  22. Schmitt, V., Zhou, X., Juliusson, K., Royer, B., Blais, A., Bertet, P., Esteve, D.: Multiplexed readout of transmon qubits with Josephson bifurcation amplifiers. Phys. Rev. A. 90, 062333 (2014)

    Article  ADS  Google Scholar 

  23. Wootton, J.R., Loss, D.: High threshold error correction for the surface code. Phys. Rev. L. 109, 160503 (2012)

    Article  ADS  Google Scholar 

  24. Varsamopoulos, S., Criger, B., Bertels, K.: Decoding small surface codes with feedforward neural networks. Quantum. Sci. Technol. 3, 015004 (2017)

    Article  ADS  Google Scholar 

  25. Delfosse, N.: Decoding color codes by projection onto surface codes. Phys. Rev. A. 89, 012317 (2014)

    Article  ADS  Google Scholar 

  26. Botsinis, P., Babar, Z., Alanis, D., Chandra, D., Nguyen, H., Ng, S.X., Hanzo, L.: Quantum error correction protects quantum search algorithms against decoherence. Sci. Rep. 6, 1–13 (2016)

    Article  Google Scholar 

  27. Qi, L., Yan, Y., Wang, G.L., Zhang, S., Wang, H.F.: Bosonic Kitaev phase in a frequency-modulated optomechanical array. Phys. Rev. A. 100, 062323 (2019)

    Article  ADS  Google Scholar 

  28. Varona, S., Martin-Delgado, M.A.: Determination of the semion code threshold using neural decoders. Phys. Rev. A. 102(3), 032411 (2020)

    Article  MathSciNet  ADS  Google Scholar 

  29. Liu, Y.H., Poulin, D.: Neural belief-propagation decoders for quantum error-correcting codes. Phys. Rev. L. 122, 200501 (2019)

    Article  ADS  Google Scholar 

  30. Zhou, N.R., Li, J.F., Yu, Z.B., Gong, L.H., Farouk, A.: New quantum dialogue protocol based on continuous-variable two-mode squeezed vacuum states. Quantum. Inf. Process. 16, 1–16 (2017)

    Article  MATH  ADS  Google Scholar 

  31. Hu, X.M., Huang, C.X., Sheng, Y.B., Zhou, L., Liu, B.H., Guo, Y., Guo, G.C.: Long-distance entanglement purification for quantum communication. Phys. Rev. L. 126, 010503 (2021)

    Article  ADS  Google Scholar 

  32. Premakumar, V.N., Sha, H., Crow, D., Bach, E., Joynt, R.: 2-designs and redundant syndrome extraction for quantum error correction. Quantum. Inf. Process. 20, 1–9 (2021)

    Article  MathSciNet  Google Scholar 

  33. Jia, Z.A., Zhang, Y.H., Wu, Y.C., Kong, L., Guo, G.C., Guo, G.P.: Efficient machine-learning representations of a surface code with boundaries, defects, domain walls, and twists. Phys. Rev. A. 99, 012307 (2019)

    Article  ADS  Google Scholar 

  34. Huang, Z., Rong, Z., Zou, X., He, Z.: Semi-quantum secure direct communication in the curved spacetime. Quantum. Inf. Process. 20, 1–12 (2021)

    Article  MathSciNet  Google Scholar 

  35. Long, G.L.: Grover algorithm with zero theoretical failure rate. Phys. Rev. A. 64, 022307 (2001)

    Article  ADS  Google Scholar 

  36. Zhou, N.R., Liu, X.X., Chen, Y.L., Du, N.S.: Quantum K-nearest-neighbor image classification algorithm based on KL transform. Int. J. Theor. Phys. 60, 1209–1224 (2021)

    Article  MATH  Google Scholar 

  37. Xu, X., Benjamin, S.C., Yuan, X.: Variational circuit compiler for quantum error correction. Phys. Rev. Appl. 15, 034068 (2021)

    Article  ADS  Google Scholar 

  38. Wootton, J.R., Loss, D.: High threshold error correction for the surface code. Phys. Rev. L. 109, 160503 (2012)

    Article  ADS  Google Scholar 

  39. Stace, T.M., Barrett, S.D., Doherty, A.C.: Thresholds for topological codes in the presence of loss. Phys. Rev. L. 102, 200501 (2009)

    Article  ADS  Google Scholar 

  40. Bai, C.H., Wang, D.Y., Zhang, S., Liu, S., Wang, H.F.: Strong mechanical squeezing in a standard optomechanical system by pump modulation. Phys. Rev. A. 101, 053836 (2020)

    Article  ADS  Google Scholar 

  41. Andreasson, P., Johansson, J., Liljestrand, S., Granath, M.: Quantum error correction for the toric code using deep reinforcement learning. Quantum. 3, 183 (2019)

    Article  Google Scholar 

  42. Song, W., Wieśniak, M., Liu, N., Pawłowski, M., Lee, J., Kim, J., Bang, J.: Tangible reduction in learning sample complexity with large classical samples and small quantum system. Quantum. Inf. Process. 20, 1–18 (2021)

    Article  MathSciNet  Google Scholar 

  43. Tuckett, D.K., Bartlett, S.D., Flammia, S.T.: Ultrahigh error threshold for surface codes with biased noise. Phys. Rev. L. 120, 050505 (2018)

    Article  ADS  Google Scholar 

  44. Laflamme, R., Miquel, C., Paz, J.P., Zurek, W.H.: Perfect quantum error correcting code. Phys. Rev. L. 77(1), 198 (1996)

    Article  ADS  Google Scholar 

  45. Liu, Y.H., Poulin, D.: Neural belief-propagation decoders for quantum error-correcting codes. Phys. Rev. L. 122(20), 200501 (2019)

    Article  ADS  Google Scholar 

  46. Clader, B.D., Trout, C.J., Barnes, J.P., Schultz, K., Quiroz, G., Titum, P.: Impact of correlations and heavy tails on quantum error correction. Phys. Rev. A. 103, 052428 (2021)

    Article  MathSciNet  ADS  Google Scholar 

Download references

Acknowledgements

We would like to thank Mr. Hongyang Ma for his careful guidance, other authors’ help and the foundations’ strong support including the National Natural Science Foundation of China (Grant Nos. 11975132, 61772295), Natural Science Foundation of Shandong Province, China (No .ZR2019YQ01), Project of Shandong Province Higher Educational Science and Technology Program (No.J18KZ012) and Shandong Provincial Natural Fund Project (No.ZR2021MF049).

Author information

Authors and Affiliations

  1. School of Information and Control Engineering, Qingdao University of Technology, Qingdao, China

    Haowen Wang, Zhaoyang Song & Yanbing Tian

  2. School of Science, Qingdao University of Technology, Qingdao, China

    Yinuo Wang & Hongyang Ma

Authors
  1. Haowen Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Zhaoyang Song
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yinuo Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Yanbing Tian
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Hongyang Ma
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Hongyang Ma.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, H., Song, Z., Wang, Y. et al. Target-generating quantum error correction coding scheme based on generative confrontation network. Quantum Inf Process 21, 280 (2022). https://doi.org/10.1007/s11128-022-03616-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-022-03616-4

Keywords