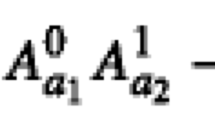Multi-nonlocality and detection of multipartite entanglements by special quantum networks

Abstract

Recently, there has been increasing attention to the study of nonlocality of quantum networks. Contrary to the standard Bell nonlocality, quantum networks concern several independent physical sources and joint measurements, from which the generated quantum correlations are fundamental for the long-distance quantum communications. This paper examines the nonlocality of a kind of special quantum network with multipartite sources. Firstly, a simple seven partite quantum network with three tripartite sources is studied in detail. A 3-local inequality is established, and the corresponding quantum violations are discussed. Then, the results are used to detect entanglement of tripartite states. Furthermore, for $n\ge 3$, the multilocal inequalities is extended to networks with $(2^n-1)$ parties and $(2^{n-1}-1)$ tripartite sources. Finally, the multilocal inequalities for more general networks with multipartite sources are also established.

Appendices

Appendix

1.1 Appendix A: Proof of Theorem 1

The following lemma from [14] is useful to prove Theorem 1 and some remaining results.

Lemma 7

[14, Lemma 1] Assume that $x_{i}^k$ are non-negative real numbers, $i=1,2,\ldots ,n$ and $k=1,2,\ldots ,m$. Then,

$$\begin{aligned} \sum \limits _{k=1}^m \left( \prod \limits _{i=1}^n x_{i}^k\right) ^{1/n} \le \prod \limits _{i=1}^n \left( \sum \limits _{k=1}^m x_{i}^k\right) ^{1/n}. \end{aligned}$$

Proof

From the assumption, all the joint probability distributions satisfy Eqs. (3)–(4). Write

$$\begin{aligned} \left\langle A^{1,1}_{x_{1}^1}\right\rangle _{\lambda _{1}}&=\sum \limits _{a_{1}^1}(-1)^{a_{1}^1} P(a_{1}^1|x_{1}^1, \lambda _{1}),\\ \langle B_{y}\rangle _{\lambda _{1},\lambda _{2}}&=\sum \limits _{b}(-1)^{b} P(b |y, \lambda _{1},\lambda _{2}),\quad \langle C_{z}\rangle _{\lambda _{1},\lambda _{3}} =\sum \limits _{c}(-1)^{c} P(c |z, \lambda _{1},\lambda _{3}),\\ \left\langle A^{2,i}_{x_{2}^i}\right\rangle _{\lambda _{2}}&=\sum \limits _{a_{2}^i}(-1)^{a_{2}^i} P(a_{2}^i|x_{2}^i, \lambda _{2}), \\ \left\langle A^{3,i}_{x_{3}^i}\right\rangle _{\lambda _{3}}&=\sum \limits _{a_{3}^i}(-1)^{a_{3}^i} P(a_{3}^i|x_{3}^i, \lambda _{3}), \quad i=1,2. \end{aligned}$$

Then,

$$\begin{aligned} K_{X}&=\frac{1}{2^{5}} \sum \limits _{\bar{x}} g(X)\left\langle A^{1,1}_{x^1_1} B_{y_{X}} C_{z_{X}} A^{2,1}_{x^1_2} A^{2,2}_{x^2_2} A^{3,1}_{x^1_3} A^{3,2}_{x^2_3} \right\rangle \nonumber \\&=\frac{1}{2^{5}} \sum \limits _{\bar{x}} g(X) \sum \limits _{a^1_1, b, c, a^1_2,\ldots , a^2_3}(-1)^{a^1_1+b+c+a^1_2+\ldots +a^2_3} \int \int \int \mathrm{d}\lambda _{1} \mathrm{d}\lambda _{2} \mathrm{d}\lambda _{3} P_{1}(\lambda _{1}) P_{2}(\lambda _{2}) P_{3}(\lambda _{3})\nonumber \\&\quad \cdot P(a^1_1|x^1_1,\lambda _{1}) P(b|y_{X},\lambda _{1},\lambda _{2}) P(c|z_{X},\lambda _{1},\lambda _{3}) P(a^1_2|x^1_2,\lambda _{2}) P(a^2_2|x^2_2,\lambda _{2}) P(a^1_3|x^1_3,\lambda _{3})\nonumber \\&\quad \cdot P(a^2_3|x^2_3,\lambda _{3})\nonumber \\&= \frac{1}{2^{5}} \sum \limits _{\bar{x}} g(X) \int \int \int \mathrm{d}\lambda _{1} \mathrm{d}\lambda _{2} \mathrm{d}\lambda _{3} P_{1}(\lambda _{1}) P_{2}(\lambda _{2}) P_{3}(\lambda _{3}) \langle A^{1,1}_{x^1_1} \rangle _{\lambda _{1}} \langle B_{y_{X}}\rangle _{\lambda _{1}, \lambda _{2}} \langle C_{z_{X}}\rangle _{\lambda _{1}, \lambda _{3}}\nonumber \\&\quad \cdot \langle A^{2,1}_{x^1_2}\rangle _{\lambda _{2}} \langle A^{2,2}_{x^2_2}\rangle _{\lambda _{2}} \langle A^{3,1}_{x^1_3}\rangle _{\lambda _{3}} \langle A^{3,2}_{x^2_3}\rangle _{\lambda _{3}}\nonumber \\&= \frac{1}{2^{5}} \sum \limits _{\bar{x}} \prod \limits _{j=1}^{3} (-1)^{ \sum \limits _{k\in X_{j}} x_j^k} \int \int \int \mathrm{d}\lambda _{1} \mathrm{d}\lambda _{2} \mathrm{d}\lambda _{3} P_{1}(\lambda _{1}) P_{2}(\lambda _{2}) P_{3}(\lambda _{3}) \langle A^{1,1}_{x^1_1} \rangle _{\lambda _{1}} \langle B_{y_{X}}\rangle _{\lambda _{1}, \lambda _{2}}\nonumber \\&\quad \cdot \langle C_{z_{X}}\rangle _{\lambda _{1}, \lambda _{3}} \langle A^{2,1}_{x^1_2}\rangle _{\lambda _{2}} \langle A^{2,2}_{x^2_2}\rangle _{\lambda _{2}} \langle A^{3,1}_{x^1_3}\rangle _{\lambda _{3}} \langle A^{3,2}_{x^2_3}\rangle _{\lambda _{3}}\nonumber \\&= \frac{1}{2^{5}} \sum \limits _{\bar{x}} \prod \limits _{j=1}^{3} (-1)^{ \sum \limits _{k} x_j^k \delta ^{k}_{X_{j}}} \int \int \int \mathrm{d}\lambda _{1} \mathrm{d}\lambda _{2} \mathrm{d}\lambda _{3} P_{1}(\lambda _{1}) P_{2}(\lambda _{2}) P_{3}(\lambda _{3}) \langle A^{1,1}_{x^1_1} \rangle _{\lambda _{1}} \langle B_{y_{X}}\rangle _{\lambda _{1}, \lambda _{2}}\nonumber \\&\quad \cdot \langle C_{z_{X}}\rangle _{\lambda _{1}, \lambda _{3}} \langle A^{2,1}_{x^1_2}\rangle _{\lambda _{2}} \langle A^{2,2}_{x^2_2}\rangle _{\lambda _{2}} \langle A^{3,1}_{x^1_3}\rangle _{\lambda _{3}} \langle A^{3,2}_{x^2_3}\rangle _{\lambda _{3}}\nonumber \\&= \int \int \int \mathrm{d}\lambda _{1} \mathrm{d}\lambda _{2} \mathrm{d}\lambda _{3} P_{1}(\lambda _{1}) P_{2}(\lambda _{2}) P_{3}(\lambda _{3}) \frac{\sum _{x^1_1}(-1)^{x^1_1 \delta ^1_{X_{1}}} \langle A^{1,1}_{x^1_1}\rangle _{\lambda _{1}}}{2} \langle B_{y_{X}}\rangle _{\lambda _{1}, \lambda _{2}} \langle C_{z_{X}}\rangle _{\lambda _{1}, \lambda _{3}}\nonumber \\&\quad \cdot \frac{\sum _{x^1_2}(-1)^{x^1_2 \delta ^1_{X_{2}}} \langle A^{2,1}_{x^1_2}\rangle _{\lambda _{2}}}{2} \frac{\sum _{x^2_2}(-1)^{x^2_2 \delta ^2_{X_{2}}} \langle A^{2,2}_{x^2_2}\rangle _{\lambda _{2}}}{2} \frac{\sum _{x^1_3}(-1)^{x^1_3 \delta ^1_{X_{3}}} \langle A^{3,1}_{x^1_3}\rangle _{\lambda _{3}}}{2}\nonumber \\&\quad \cdot \frac{\sum _{x^3_3}(-1)^{x^2_3 \delta ^2_{X_{3}}} \langle A^{3,3}_{x^2_3}\rangle _{\lambda _{3}}}{2}\nonumber \\&= \int \int \int \mathrm{d}\lambda _{1} \mathrm{d}\lambda _{2} \mathrm{d}\lambda _{3} P_{1}(\lambda _{1}) P_{2}(\lambda _{2}) P_{3}(\lambda _{3}) \frac{\langle A^{1,1}_{0}\rangle _{\lambda _{1}}+(-1)^{ \delta ^1_{X_{1}}}\langle A^{1,1}_{1}\rangle _{\lambda _{1}} }{2} \langle B_{y_{X}}\rangle _{\lambda _{1}, \lambda _{2}} \langle C_{z_{X}}\rangle _{\lambda _{1}, \lambda _{3}}\nonumber \\&\quad \cdot \frac{ \langle A^{2,1}_{0}\rangle _{\lambda _{2}}+ (-1)^{ \delta ^1_{X_{2}}} \langle A^{2,1}_{1}\rangle _{\lambda _{2}}}{2} \frac{ \langle A^{2,2}_{0}\rangle _{\lambda _{2}}+ (-1)^{ \delta ^2_{X_{2}}} \langle A^{2,2}_{1}\rangle _{\lambda _{2}}}{2}\nonumber \\&\quad \cdot \frac{ \langle A^{3,1}_{0}\rangle _{\lambda _{3}}+ (-1)^{ \delta ^1_{X_{3}}} \langle A^{3,1}_{1}\rangle _{\lambda _{3}}}{2} \frac{ \langle A^{3,2}_{0}\rangle _{\lambda _{3}}+ (-1)^{ \delta ^2_{X_{3}}} \langle A^{3,2}_{1}\rangle _{\lambda _{3}}}{2}, \end{aligned}$$

(A1)

where $\delta ^{k}_{X_{j}}=1$ if $k\in X_{j}$, $\delta ^{k}_{X_{j}}=0$ if $k\notin X_{j}$, $\forall j=1,2,3$. Note that $|\langle B_{y_{X}}\rangle _{\lambda _{1}, \lambda _{2}}| \le 1$ and $|\langle C_{z_{X}}\rangle _{\lambda _{1}, \lambda _{3}} | \le 1$. Thus Eq. (A1) implies

$$\begin{aligned} |K_{X}|&\le \int \int \int \mathrm{d}\lambda _{1} \mathrm{d}\lambda _{2} \mathrm{d}\lambda _{3} P_{1}(\lambda _{1}) P_{2}(\lambda _{2}) P_{3}(\lambda _{3}) \left| \frac{\langle A^{1,1}_{0}\rangle _{\lambda _{1}}+(-1)^{ \delta ^1_{X_{1}}}\langle A^{1,1}_{1}\rangle _{\lambda _{1}} }{2}\right| \\&\quad \cdot |\langle B_{y_{X}}\rangle _{\lambda _{1}, \lambda _{2}}| |\langle C_{z_{X}}\rangle _{\lambda _{1}, \lambda _{3}}|\\&\quad \cdot \left| \frac{ \langle A^{2,1}_{0}\rangle _{\lambda _{2}}+ (-1)^{ \delta ^1_{X_{2}}} \langle A^{2,1}_{1}\rangle _{\lambda _{2}}}{2}\right| \left| \frac{ \langle A^{2,2}_{0}\rangle _{\lambda _{2}}+ (-1)^{ \delta ^2_{X_{2}}} \langle A^{2,2}_{1}\rangle _{\lambda _{2}}}{2}\right| \\&\quad \cdot \left| \frac{ \langle A^{3,1}_{0}\rangle _{\lambda _{3}}+ (-1)^{ \delta ^1_{X_{3}}} \langle A^{3,1}_{1}\rangle _{\lambda _{3}}}{2}\right| \left| \frac{ \langle A^{3,2}_{0}\rangle _{\lambda _{3}}+ (-1)^{ \delta ^2_{X_{3}}} \langle A^{3,2}_{1}\rangle _{\lambda _{3}}}{2}\right| \\&\le \int \int \int \mathrm{d}\lambda _{1} \mathrm{d}\lambda _{2} \mathrm{d}\lambda _{3} P_{1}(\lambda _{1}) P_{2}(\lambda _{2}) P_{3}(\lambda _{3}) \left| \frac{\langle A^{1,1}_{0}\rangle _{\lambda _{1}}+(-1)^{ \delta ^1_{X_{1}}}\langle A^{1,1}_{1}\rangle _{\lambda _{1}} }{2}\right| \\&\quad \cdot \left| \frac{ \langle A^{2,1}_{0}\rangle _{\lambda _{2}}+ (-1)^{ \delta ^1_{X_{2}}} \langle A^{2,1}_{1}\rangle _{\lambda _{2}}}{2}\right| \\&\quad \cdot \left| \frac{ \langle A^{2,2}_{0}\rangle _{\lambda _{2}}+ (-1)^{ \delta ^2_{X_{2}}} \langle A^{2,2}_{1}\rangle _{\lambda _{2}}}{2}\right| \left| \frac{ \langle A^{3,1}_{0}\rangle _{\lambda _{3}}+ (-1)^{ \delta ^1_{X_{3}}} \langle A^{3,1}_{1}\rangle _{\lambda _{3}}}{2}\right| \\&\quad \cdot \left| \frac{ \langle A^{3,2}_{0}\rangle _{\lambda _{3}}+ (-1)^{ \delta ^2_{X_{3}}} \langle A^{3,2}_{1}\rangle _{\lambda _{3}}}{2}\right| \\&= \left( \int \mathrm{d}\lambda _{1} P_{1}(\lambda _{1}) |\frac{\langle A^{1,1}_{0}\rangle _{\lambda _{1}}+(-1)^{ \delta ^1_{X_{1}}}\langle A^{1,1}_{1}\rangle _{\lambda _{1}} }{2}|\right) \\&\quad \cdot \left( \int \mathrm{d}\lambda _{2} P_{2}(\lambda _{2}) \left| \frac{ \langle A^{2,1}_{0}\rangle _{\lambda _{2}}+ (-1)^{ \delta ^1_{X_{2}}} \langle A^{2,1}_{1}\rangle _{\lambda _{2}}}{2}\right| \left| \frac{ \langle A^{2,2}_{0}\rangle _{\lambda _{2}}+ (-1)^{ \delta ^2_{X_{2}}} \langle A^{2,2}_{1}\rangle _{\lambda _{2}}}{2}\right| \right) \\&\quad \cdot \left( \int \mathrm{d}\lambda _{3} P_{3}(\lambda _{3}) \left| \frac{ \langle A^{3,1}_{0}\rangle _{\lambda _{3}}+ (-1)^{ \delta ^1_{X_{3}}} \langle A^{3,1}_{1}\rangle _{\lambda _{3}}}{2}\right| \left| \frac{ \langle A^{3,2}_{0}\rangle _{\lambda _{3}}+ (-1)^{ \delta ^2_{X_{3}}} \langle A^{3,2}_{1}\rangle _{\lambda _{3}}}{2}\right| \right) . \end{aligned}$$

Using Lemma 7, we obtain that

$$\begin{aligned} \sum \limits _{X\in \mathbb {P}(\mathbb {N}_{L})} |K_{X}|^{\frac{1}{3}}&\le \left( \int \mathrm{d}\lambda _{1} P_{1}(\lambda _{1}) \sum \limits _{X\in \mathbb {P}(\mathbb {N}_{L})} \left| \frac{\langle A^{1,1}_{0}\rangle _{\lambda _{1}}+(-1)^{ \delta ^1_{X_{1}}}\langle A^{1,1}_{1}\rangle _{\lambda _{1}} }{2}\right| \right) ^{\frac{1}{3}}\nonumber \\&\quad \cdot \left( \int \mathrm{d}\lambda _{2} P_{2}(\lambda _{2}) \sum \limits _{X\in \mathbb {P}(\mathbb {N}_{L})} \left| \frac{ \langle A^{2,1}_{0}\rangle _{\lambda _{2}}+ (-1)^{ \delta ^1_{X_{2}}} \langle A^{2,1}_{1}\rangle _{\lambda _{2}}}{2}\right| \right. \nonumber \\&\quad \cdot \left. \left| \frac{ \langle A^{2,2}_{0}\rangle _{\lambda _{2}}+ (-1)^{ \delta ^2_{X_{2}}} \langle A^{2,2}_{1}\rangle _{\lambda _{2}}}{2}\right| \right) ^{\frac{1}{3}}\nonumber \\&\quad \cdot \left( \int \mathrm{d}\lambda _{3} P_{3}(\lambda _{3}) \sum \limits _{X\in \mathbb {P}(\mathbb {N}_{L})} \left| \frac{ \langle A^{3,1}_{0}\rangle _{\lambda _{3}}+ (-1)^{ \delta ^1_{X_{3}}} \langle A^{3,1}_{1}\rangle _{\lambda _{3}}}{2}\right| \right. \nonumber \\&\quad \cdot \left. \left| \frac{ \langle A^{3,2}_{0}\rangle _{\lambda _{3}}+ (-1)^{ \delta ^2_{X_{3}}} \langle A^{3,2}_{1}\rangle _{\lambda _{3}}}{2}\right| \right) ^{\frac{1}{3}}. \end{aligned}$$

(A2)

Next, we separately consider three factors in the right hand of inequality (A2). It is known that $X\in \mathbb {P}(\mathbb {N}_{L})= \mathbb {P}(\{1,2\}) =\{\emptyset , \{1\}, \{2\}, \{1,2\} \}$. Thus, in the right hand of inequality (A2), the first factor reduces to

$$\begin{aligned}&\int \mathrm{d}\lambda _{1} P_{1}(\lambda _{1}) \sum \limits _{X\in \mathbb {P}(\mathbb {N}_{L})} \left| \frac{\langle A^{1,1}_{0}\rangle _{\lambda _{1}}+(-1)^{ \delta ^1_{X_{1}}}\langle A^{1,1}_{1}\rangle _{\lambda _{1}} }{2}\right| \\&\quad = \int \mathrm{d}\lambda _{1} P_{1}(\lambda _{1}) \left( \left| \frac{\langle A^{1,1}_{0}\rangle _{\lambda _{1}}+\langle A^{1,1}_{1}\rangle _{\lambda _{1}} }{2}\right| +\left| \frac{\langle A^{1,1}_{0}\rangle _{\lambda _{1}}-\langle A^{1,1}_{1}\rangle _{\lambda _{1}} }{2}\right| \right. \\&\qquad +\left. \left| \frac{\langle A^{1,1}_{0}\rangle _{\lambda _{1}}+\langle A^{1,1}_{1}\rangle _{\lambda _{1}} }{2}\right| +\left| \frac{\langle A^{1,1}_{0}\rangle _{\lambda _{1}}-\langle A^{1,1}_{1}\rangle _{\lambda _{1}} }{2}\right| \right) \\&\quad = \int \mathrm{d}\lambda _{1} P_{1}(\lambda _{1})\cdot 2\max \{|\langle A^{1,1}_{0}\rangle _{\lambda _{1}}|, |\langle A^{1,1}_{1}\rangle _{\lambda _{1}} | \} \le 2; \end{aligned}$$

the second factor reduces to

$$\begin{aligned}&\int \mathrm{d}\lambda _{2} P_{2}(\lambda _{2}) \sum \limits _{X\in \mathbb {P}(\mathbb {N}_{L})} \left| \frac{ \langle A^{2,1}_{0}\rangle _{\lambda _{2}}+ (-1)^{ \delta ^1_{X_{2}}} \langle A^{2,1}_{1}\rangle _{\lambda _{2}}}{2}\right| \left| \frac{ \langle A^{2,2}_{0}\rangle _{\lambda _{2}}+ (-1)^{ \delta ^2_{X_{2}}} \langle A^{2,2}_{1}\rangle _{\lambda _{2}}}{2}\right| \\&\quad = \int \mathrm{d}\lambda _{2} P_{2}(\lambda _{2}) \left( \left| \frac{\langle A^{2,1}_{0}\rangle _{\lambda _{2}}+\langle A^{2,1}_{1}\rangle _{\lambda _{2}} }{2}\right| \left| \frac{\langle A^{2,2}_{0}\rangle _{\lambda _{2}}+\langle A^{2,2}_{1}\rangle _{\lambda _{2}} }{2}\right| \right. \\&\qquad +\left. \left| \frac{\langle A^{2,1}_{0}\rangle _{\lambda _{2}}-\langle A^{2,1}_{1}\rangle _{\lambda _{2}} }{2}\right| \left| \frac{\langle A^{2,2}_{0}\rangle _{\lambda _{2}}+\langle A^{2,2}_{1}\rangle _{\lambda _{2}} }{2}\right| \right. \\&\qquad +\left. \left| \frac{\langle A^{2,1}_{0}\rangle _{\lambda _{2}}+\langle A^{2,1}_{1}\rangle _{\lambda _{2}} }{2}\right| \left| \frac{\langle A^{2,2}_{0}\rangle _{\lambda _{2}}-\langle A^{2,2}_{1}\rangle _{\lambda _{2}} }{2}\right| \right. \\&\qquad +\left. \left| \frac{\langle A^{2,1}_{0}\rangle _{\lambda _{2}}-\langle A^{2,1}_{1}\rangle _{\lambda _{2}} }{2}\right| \left| \frac{\langle A^{2,2}_{0}\rangle _{\lambda _{2}}-\langle A^{2,2}_{1}\rangle _{\lambda _{2}} }{2}\right| \right) \\&\quad = \int \mathrm{d}\lambda _{2} P_{2}(\lambda _{2}) \left( \left| \frac{\langle A^{2,1}_{0}\rangle _{\lambda _{2}}+\langle A^{2,1}_{1}\rangle _{\lambda _{2}} }{2}\right| + \left| \frac{\langle A^{2,1}_{0}\rangle _{\lambda _{2}}-\langle A^{2,1}_{1}\rangle _{\lambda _{2}} }{2}\right| \right) \\&\qquad \cdot \left( \left| \frac{\langle A^{2,2}_{0}\rangle _{\lambda _{2}}+\langle A^{2,2}_{1}\rangle _{\lambda _{2}} }{2}\right| + \left| \frac{\langle A^{2,2}_{0}\rangle _{\lambda _{2}}-\langle A^{2,2}_{1}\rangle _{\lambda _{2}} }{2}\right| \right) \\&\quad = \int \mathrm{d}\lambda _{2} P_{2}(\lambda _{2}) \max \{|\langle A^{2,1}_{0}\rangle _{\lambda _{2}}|, |\langle A^{2,1}_{1}\rangle _{\lambda _{2}} | \} \max \{|\langle A^{2,2}_{0}\rangle _{\lambda _{2}}|, |\langle A^{2,2}_{1}\rangle _{\lambda _{2}} | \} \le 1; \end{aligned}$$

and similarly, the third factor reduces to

$$\begin{aligned} \int \mathrm{d}\lambda _{3} P_{3}(\lambda _{3}) \sum \limits _{X\in \mathbb {P}(\mathbb {N}_{L})} \left| \frac{ \langle A^{3,1}_{0}\rangle _{\lambda _{3}}+ (-1)^{ \delta ^1_{X_{3}}} \langle A^{3,1}_{1}\rangle _{\lambda _{3}}}{2}\right| \left| \frac{ \langle A^{3,2}_{0}\rangle _{\lambda _{3}}+ (-1)^{ \delta ^2_{X_{3}}} \langle A^{3,2}_{1}\rangle _{\lambda _{3}}}{2}\right| \le 1. \end{aligned}$$

Inserting the above results into inequality (A2), one gets $\sum _{X\in \mathbb {P}(\mathbb {N}_{L})} |K_{X}|^{\frac{1}{3}} \le 2^{\frac{1}{3}}$, as desired. $\square$

1.2 Appendix B: Proof of Propositions 3–4

Observe that for any $X\in \mathbb {P}(\mathbb {N}_L)$, one has

$$\begin{aligned} K_{X}&\!=\! \frac{1}{2^{5}} \sum \limits _{\bar{x}} g(X) \sum \limits _{a^1_1, b, c, a^1_2,\ldots , a^2_3}(-1)^{a^1_1+b+c+a^1_2+\cdots +a^2_3} P(a^1_1,b, c, a^1_{2}, \ldots , a^2_{3}| x^1_1, y_{X}, z_{X}, x^1_{2}, \ldots , x^2_{3})\nonumber \\&= \frac{1}{2^{5}} \sum \limits _{\bar{x}} g(X) \sum \limits _{a^1_1, b, c, a^1_2,\ldots , a^2_3}(-1)^{a^1_1+b+c+a^1_2+\cdots +a^2_3} \mathrm {tr} \big [\big (M_{a^1_1 |x^1_1} \otimes M_{b|y_{X}} \otimes M_{c|z_{X}} \otimes M_{a^1_2 |x^1_2} \nonumber \\&\quad \otimes M_{a^2_2 |x^2_2} \otimes M_{a^1_3 |x^1_3} \otimes M_{a^2_3 |x^2_3})(\rho _{1}\otimes \rho _{2}\otimes \rho _{3} \big )\big ]\nonumber \\&= \frac{1}{2^{5}} \sum \limits _{\bar{x}} g(X) \mathrm {tr} \big [\big ((M_{0 |x^1_1}- M_{1 |x^1_1}) \otimes (M_{0|y_{X}}- M_{1|y_{X}}) \otimes (M_{0|z_{X}}- M_{1|z_{X}}) \nonumber \\&\quad \otimes (M_{0 |x^1_2}- M_{1 |x^1_2}) \otimes (M_{0 |x^2_2}- M_{1 |x^2_2}) \otimes (M_{0 |x^1_3}- M_{1 |x^1_3}) \otimes (M_{0 |x^2_3}- M_{1 |x^2_3})\big )\nonumber \\&\quad \cdot (\rho _{1}\otimes \rho _{2}\otimes \rho _{3} )\big ]\nonumber \\&= \frac{1}{2^{5}} \sum \limits _{\bar{x}} g(X) \mathrm {tr} \big [\big (A^{1,1}_{x_1^1} \otimes B_{y_{X}} \otimes C_{z_{X}} \otimes A^{2,1}_{x_2^1} \otimes A^{2,2}_{x_2^2} \otimes A^{3,1}_{x_3^1} \otimes A^{3,2}_{x_3^2}\big ) (\rho _{1}\otimes \rho _{2}\otimes \rho _{3})\big ]\nonumber \\&= \frac{1}{2^{5}} \sum \limits _{\bar{x}} \prod \limits _{j=1}^{3} (-1)^{ \sum \limits _{k\in X_{j}} x_j^k} \mathrm {tr} [(A^{1,1}_{x_1^1} \otimes B_{y_{X}} \otimes C_{z_{X}} \otimes A^{2,1}_{x_2^1} \otimes \cdots \otimes A^{3,2}_{x_3^2}) (\rho _{1}\otimes \rho _{2}\otimes \rho _{3})]\nonumber \\&= \frac{1}{2^{5}} \sum \limits _{\bar{x}} \prod \limits _{j=1}^{3} (-1)^{ \sum \limits _{k} x_j^k \delta ^{k}_{X_{j}}} \mathrm {tr} \big [\big (A^{1,1}_{x_1^1} \otimes B_{y_{X}} \otimes C_{z_{X}} \otimes A^{2,1}_{x_2^1} \otimes \cdots \otimes A^{3,2}_{x_3^2}\big ) (\rho _{1}\otimes \rho _{2}\otimes \rho _{3})\big ]\nonumber \\&= \frac{1}{2^{5}} \mathrm {tr} \big [\big ((A^{1,1}_{0}+ (-1)^{\delta ^1_{X_{1}}}A^{1,1}_{1} ) \otimes B_{y_{X}} \otimes C_{z_{X}} \otimes (A^{2,1}_{0}+ (-1)^{\delta ^1_{X_{2}}}A^{2,1}_{1} )\nonumber \\&\quad \otimes (A^{2,2}_{0}+ (-1)^{\delta ^2_{X_{2}}}A^{2,2}_{1} )\otimes (A^{3,1}_{0}+ (-1)^{\delta ^1_{X_{3}}}A^{3,1}_{1} )\otimes (A^{3,2}_{0}+ (-1)^{\delta ^2_{X_{3}}}A^{3,2}_{1} )\big ) (\rho _{1}\otimes \rho _{2}\otimes \rho _{3})\big ]\nonumber \\&= \mathrm {tr} \bigg [\bigg (\frac{A^{1,1}_{0}+ (-1)^{\delta ^1_{X_{1}}}A^{1,1}_{1} }{2} \otimes B_{y_{X}} \otimes C_{z_{X}} \otimes \frac{A^{2,1}_{0}+ (-1)^{\delta ^1_{X_{2}}}A^{2,1}_{1} }{2}\otimes \frac{A^{2,2}_{0}+ (-1)^{\delta ^2_{X_{2}}}A^{2,2}_{1} }{2}\nonumber \\&\quad \otimes \frac{A^{3,1}_{0}+ (-1)^{\delta ^1_{X_{3}}}A^{3,1}_{1} }{2}\otimes \frac{A^{3,2}_{0}+ (-1)^{\delta ^2_{X_{3}}}A^{3,2}_{1} }{2}\bigg ) (\rho _{1}\otimes \rho _{2}\otimes \rho _{3})\bigg ], \end{aligned}$$

(A3)

where $\delta ^{k}_{X_{j}}=1$ if $k\in X_{j}$, $\delta ^{k}_{X_{j}}=0$ if $k\notin X_{j}$, $\forall j=1,2,3$.

Proof of Proposition 3

Suppose that each source $S_i$ $(i=1,2,3)$ produces arbitrary fully separable state $\rho _i$. Write $\rho _1= \sum _{k} p_{k}^{(1)} (\rho _{k}^{(11)} \otimes \rho _{k}^{(12)}\otimes \rho _{k}^{(13)})$, $\rho _2= \sum _{h} p_{h}^{(2)} (\rho _{h}^{(21)} \otimes \rho _{h}^{(22)}\otimes \rho _{h}^{(23)})$ and $\rho _3= \sum _{l} p_{l}^{(3)} (\rho _{l}^{(31)} \otimes \rho _{l}^{(32)}\otimes \rho _{l}^{(33)})$, where $p_{k}^{(1)} >0$, $\sum _{k} p_{k}^{(1)}=1$, $p_{h}^{(2)}>0$, $\sum _{h} p_{h}^{(2)}=1$, $p_{l}^{(3)}>0$, $\sum _{l} p_{l}^{(3)}=1$. We will prove that these states altogether do not violate the inequality (5).

Indeed, by (A3), for these fully separable states $\rho _i$, we have

Since $|\mathrm {tr} [B_{y_{X}} (\rho _{k}^{(12)}\otimes \rho _{h}^{(21)})]|= |P(0|y_X)- P(1|y_X)| \le 1$ and $|\mathrm {tr} [C_{z_{X}} (\rho _{k}^{(13)}\otimes \rho _{l}^{(31)})]|\le 1$ hold for arbitrary X, we then have

which implies

$$\begin{aligned} |K_{\emptyset }|&\le \left[ \sum _{k} p_{k}^{(1)} \left| \mathrm {tr} \left( \frac{A^{1,1}_{0}+ A^{1,1}_{1} }{2} \rho _{k}^{(11)}\right) \right| \right] \cdot \left[ \sum _{h} p_{h}^{(2)} \left| \mathrm {tr} \left( \frac{A^{2,1}_{0}+ A^{2,1}_{1} }{2} \rho _{h}^{(22)}\right) \right| \right. \\&\quad \cdot \left. \left| \mathrm {tr} \left( \frac{A^{2,2}_{0}+ A^{2,2}_{1} }{2} \rho _{h}^{(23)}\right) \right| \right] \\&\quad \cdot \left[ \sum _{l} p_{l}^{(3)} \left| \mathrm {tr} \left( \frac{A^{3,1}_{0}+ A^{3,1}_{1} }{2} \rho _{l}^{(32)}\right) \right| \cdot \left| \mathrm {tr} \left( \frac{A^{3,2}_{0}+ A^{3,2}_{1} }{2} \rho _{l}^{(33)}\right) \right| \right] ,\\ |K_{\{1\}}|&\le \left[ \sum _{k} p_{k}^{(1)} \left| \mathrm {tr} \left( \frac{A^{1,1}_{0}- A^{1,1}_{1} }{2} \rho _{k}^{(11)}\right) \right| \right] \cdot \left[ \sum _{h} p_{h}^{(2)} \left| \mathrm {tr} \left( \frac{A^{2,1}_{0}- A^{2,1}_{1} }{2} \rho _{h}^{(22)}\right) \right| \right. \\&\quad \cdot \left. \left| \mathrm {tr} \left( \frac{A^{2,2}_{0}+ A^{2,2}_{1} }{2} \rho _{h}^{(23)}\right) \right| \right] \\&\quad \cdot \left[ \sum _{l} p_{l}^{(3)} \left| \mathrm {tr} \left( \frac{A^{3,1}_{0}- A^{3,1}_{1} }{2} \rho _{l}^{(32)}\right) \right| \cdot \left| \mathrm {tr} \left( \frac{A^{3,2}_{0}+ A^{3,2}_{1} }{2} \rho _{l}^{(33)}\right) \right| \right] ,\\ |K_{\{2\}}|&\le \left[ \sum _{k} p_{k}^{(1)} \left| \mathrm {tr} \left( \frac{A^{1,1}_{0}+ A^{1,1}_{1} }{2} \rho _{k}^{(11)}\right) \right| \right] \cdot \left[ \sum _{h} p_{h}^{(2)} \left| \mathrm {tr} \left( \frac{A^{2,1}_{0}+ A^{2,1}_{1} }{2} \rho _{h}^{(22)}\right) \right| \right. \\&\quad \cdot \left. \left| \mathrm {tr} \left( \frac{A^{2,2}_{0}- A^{2,2}_{1} }{2} \rho _{h}^{(23)}\right) \right| \right] \\&\quad \cdot \left[ \sum _{l} p_{l}^{(3)} \left| \mathrm {tr} \left( \frac{A^{3,1}_{0}+ A^{3,1}_{1} }{2} \rho _{l}^{(32)}\right) \right| \cdot \left| \mathrm {tr} \left( \frac{A^{3,2}_{0}- A^{3,2}_{1} }{2} \rho _{l}^{(33)}\right) \right| \right] \end{aligned}$$

and

$$\begin{aligned} |K_{\{1,2\}}|&\le \left[ \sum _{k} p_{k}^{(1)} \left| \mathrm {tr} \left( \frac{A^{1,1}_{0}- A^{1,1}_{1} }{2} \rho _{k}^{(11)}\right) \right| \right] \cdot \left[ \sum _{h} p_{h}^{(2)} \left| \mathrm {tr} \left( \frac{A^{2,1}_{0}- A^{2,1}_{1} }{2} \rho _{h}^{(22)}\right) \right| \right. \\&\quad \cdot \left. \left| \mathrm {tr} \left( \frac{A^{2,2}_{0}- A^{2,2}_{1} }{2} \rho _{h}^{(23)}\right) \right| \right] \\&\quad \cdot \left[ \sum _{l} p_{l}^{(3)} \left| \mathrm {tr} \left( \frac{A^{3,1}_{0}- A^{3,1}_{1} }{2} \rho _{l}^{(32)}\right) \right| \cdot \left| \mathrm {tr} \left( \frac{A^{3,2}_{0}- A^{3,2}_{1} }{2} \rho _{l}^{(33)}\right) \right| \right] . \end{aligned}$$

It follows from Lemma 7 that

$$\begin{aligned}&\sum \limits _{X\in \mathbb {P}(\mathbb {N}_{L})} |K_{X}|^{\frac{1}{3}} = |K_{\emptyset }|^{\frac{1}{3}}+ |K_{\{1\}}|^{\frac{1}{3}}+ |K_{\{2\}}|^{\frac{1}{3}}+ |K_{\{1,2\}}|^{\frac{1}{3}}\\&\quad \le \left\{ \sum _{k} p_{k}^{(1)} \left[ 2\left| \mathrm {tr} \left( \frac{A^{1,1}_{0}+ A^{1,1}_{1} }{2} \rho _{k}^{(11)}\right) \right| + 2\left| \mathrm {tr} \left( \frac{A^{1,1}_{0}- A^{1,1}_{1} }{2} \rho _{k}^{(11)}\right) \right| \right] \right\} ^{\frac{1}{3}}\\&\qquad \cdot \left\{ \sum _{h} p_{h}^{(2)} \left[ \left| \mathrm {tr} \left( \frac{A^{2,1}_{0}+ A^{2,1}_{1} }{2} \rho _{h}^{(22)}\right) \right| \cdot \left| \mathrm {tr} \left( \frac{A^{2,2}_{0}+ A^{2,2}_{1} }{2} \rho _{h}^{(23)}\right) \right| + \left| \mathrm {tr} \left( \frac{A^{2,1}_{0}- A^{2,1}_{1} }{2} \rho _{h}^{(22)}\right) \right| \right. \right. \\&\qquad \cdot \left| \mathrm {tr} \left( \frac{A^{2,2}_{0}+ A^{2,2}_{1} }{2} \rho _{h}^{(23)}\right) \right| \\&\qquad +\left| \mathrm {tr} \left( \frac{A^{2,1}_{0}+ A^{2,1}_{1} }{2} \rho _{h}^{(22)}\right) \right| \cdot \left| \mathrm {tr} \left( \frac{A^{2,2}_{0}- A^{2,2}_{1} }{2} \rho _{h}^{(23)}\right) \right| + \left| \mathrm {tr} \left( \frac{A^{2,1}_{0}- A^{2,1}_{1} }{2} \rho _{h}^{(22)}\right) \right| \\&\qquad \left. \left. \cdot \left| \mathrm {tr} \left( \frac{A^{2,2}_{0}- A^{2,2}_{1} }{2} \rho _{h}^{(23)}\right) \right| \right] \right\} ^{\frac{1}{3}}\\&\qquad \cdot \left\{ \sum _{l} p_{l}^{(3)} \left[ \left| \mathrm {tr} \left( \frac{A^{3,1}_{0}+ A^{3,1}_{1} }{2} \rho _{l}^{(32)}\right) \right| \cdot \left| \mathrm {tr} \left( \frac{A^{3,2}_{0}+ A^{3,2}_{1} }{2} \rho _{l}^{(33)}\right) \right| + \left| \mathrm {tr} \left( \frac{A^{3,1}_{0}- A^{3,1}_{1} }{2} \rho _{l}^{(32)}\right) \right| \right. \right. \\&\qquad \cdot \left| \mathrm {tr} \left( \frac{A^{3,2}_{0}+ A^{3,2}_{1} }{2} \rho _{l}^{(33)}\right) \right| \\&\qquad \left. \left. +\left| \mathrm {tr} \left( \frac{A^{3,1}_{0}+ A^{3,1}_{1} }{2} \rho _{l}^{(32)}\right) \right| \cdot \left| \mathrm {tr} \left( \frac{A^{3,2}_{0}- A^{3,2}_{1} }{2} \rho _{l}^{(33)}\right) \right| + \left| \mathrm {tr} \left( \frac{A^{3,1}_{0}- A^{3,1}_{1} }{2} \rho _{l}^{(32)}\right) \right| \right. \right. \\&\qquad \left. \left. \cdot \left| \mathrm {tr} \left( \frac{A^{3,2}_{0}- A^{3,2}_{1} }{2} \rho _{l}^{(33)}\right) \right| \right] \right\} ^{\frac{1}{3}}\\&\quad = \left( \sum _{k} p_{k}^{(1)} 2\max \left\{ |\mathrm {tr} (A^{1,1}_{0} \rho _{k}^{(11)})|, |\mathrm {tr} (A^{1,1}_{1} \rho _{k}^{(11)})|\right\} \right) ^{\frac{1}{3}}\\&\qquad \cdot \left\{ \sum _{h} p_{h}^{(2)} \left[ \left| \mathrm {tr} \left( \frac{A^{2,1}_{0}+A^{2,1}_{1} }{2} \rho _{h}^{(22)}\right) \right| + \left| \mathrm {tr} \left( \frac{A^{2,1}_{0}-A^{2,1}_{1} }{2} \rho _{h}^{(22)}\right) \right| \right] \cdot \left[ \left| \mathrm {tr} \left( \frac{A^{2,2}_{0}+A^{2,2}_{1} }{2} \rho _{h}^{(23)}\right) \right| \right. \right. \\&\qquad \left. \left. + \left| \mathrm {tr} \left( \frac{A^{2,2}_{0}-A^{2,2}_{1} }{2} \rho _{h}^{(23)}\right) \right| \right] \right\} ^{\frac{1}{3}}\\&\qquad \cdot \left\{ \sum _{l} p_{l}^{(3)} \left[ \left| \mathrm {tr} \left( \frac{A^{3,1}_{0}+A^{3,1}_{1} }{2} \rho _{l}^{(32)}\right) \right| + \left| \mathrm {tr} \left( \frac{A^{3,1}_{0}-A^{3,1}_{1} }{2} \rho _{l}^{(32)}\right) \right| \right] \cdot \left[ \left| \mathrm {tr} \left( \frac{A^{3,2}_{0}+A^{3,2}_{1} }{2} \rho _{l}^{(33)}\right) \right| \right. \right. \\&\qquad \left. \left. + \left| \mathrm {tr} \left( \frac{A^{3,2}_{0}-A^{3,2}_{1} }{2} \rho _{l}^{(33)}\right) \right| \right] \right\} ^{\frac{1}{3}}\\&= \left( \sum _{k} p_{k}^{(1)} 2\max \{|\mathrm {tr} (A^{1,1}_{0} \rho _{k}^{(11)})|, |\mathrm {tr} (A^{1,1}_{1} \rho _{k}^{(11)})|\}\right) ^{\frac{1}{3}}\\&\qquad \cdot \left( \sum _{h} p_{h}^{(2)} \max \{|\mathrm {tr} (A^{2,1}_{0} \rho _{h}^{(22)})|, |\mathrm {tr} (A^{2,1}_{1} \rho _{h}^{(22)})|\} \cdot \max \{|\mathrm {tr} (A^{2,2}_{0} \rho _{h}^{(23)})|, |\mathrm {tr} (A^{2,2}_{1} \rho _{h}^{(23)})|\}\right) ^{\frac{1}{3}}\\&\qquad \cdot \left( \sum _{l} p_{l}^{(3)} \max \{|\mathrm {tr} (A^{3,1}_{0} \rho _{l}^{(32)})|, |\mathrm {tr} (A^{3,1}_{1} \rho _{l}^{(32)})|\} \cdot \max \{|\mathrm {tr} (A^{3,2}_{0} \rho _{l}^{(33)})|, |\mathrm {tr} (A^{3,2}_{1} \rho _{l}^{(33)})|\}\right) ^{\frac{1}{3}} \le 2^{\frac{1}{3}}, \end{aligned}$$

where the last inequality holds as $|\mathrm {tr} (A^{1,1}_{0} \rho _{k}^{(11)})|\le 1$, $|\mathrm {tr} (A^{1,1}_{1} \rho _{k}^{(11)})|\le 1$, $|\mathrm {tr} (A^{2,1}_{0} \rho _{h}^{(22)})|\le 1$, $|\mathrm {tr} (A^{2,1}_{1} \rho _{h}^{(22)})|\le 1$, $|\mathrm {tr} (A^{2,2}_{0} \rho _{h}^{(23)})| \le 1$, $|\mathrm {tr} (A^{2,2}_{1} \rho _{h}^{(23)})| \le 1$, $|\mathrm {tr} (A^{3,1}_{0} \rho _{l}^{(32)})|\le 1$, $|\mathrm {tr} (A^{3,1}_{1} \rho _{l}^{(32)})|\le 1$, $|\mathrm {tr} (A^{3,2}_{0} \rho _{l}^{(33)})|\le 1$ and $|\mathrm {tr} (A^{3,2}_{1} \rho _{l}^{(33)})|\le 1$. This yields that the overall network state $\rho =\rho _1\otimes \rho _2\otimes \rho _3$ obeys the 3-local inequality (5). $\square$

Proof of Proposition  4

Assume that the source $S_1$ produces $(A^{1,1}|BC)$ biseparable entangled state $\rho _1=\sum _{k} p_{k}^{(1)} (\rho _{k}^{(11)}\otimes \rho _{k}^{(123)})$, and the sources $S_2$, $S_3$ produce arbitrary fully separable states $\rho _2=\sum _{h} p_{h}^{(2)}(\rho _{h}^{(21)}\otimes \rho _{h}^{(22)}\otimes \rho _{h}^{(23)})$, $\rho _3=\sum _{l} p_{l}^{(3)} (\rho _{l}^{(31)}\otimes \rho _{l}^{(32)}\otimes \rho _{l}^{(33)})$, where $p_{k}^{(1)} >0$, $\sum _{k} p_{k}^{(1)}=1$, $p_{h}^{(2)}>0$, $\sum _{h} p_{h}^{(2)}=1$, $p_{l}^{(3)}>0$, $\sum _{l} p_{l}^{(3)}=1$.

In this case, Eq. (A3) reduces to

$$\begin{aligned} K_{X}&= \mathrm {tr} \left\{ \left( \frac{A^{1,1}_{0}+ (-1)^{\delta ^1_{X_{1}}}A^{1,1}_{1} }{2} \otimes B_{y_{X}} \otimes C_{z_{X}} \otimes \frac{A^{2,1}_{0}+ (-1)^{\delta ^1_{X_{2}}}A^{2,1}_{1} }{2}\right. \right. \\&\quad \otimes \frac{A^{2,2}_{0}+ (-1)^{\delta ^2_{X_{2}}}A^{2,2}_{1} }{2}\\&\quad \left. \otimes \frac{A^{3,1}_{0}+ (-1)^{\delta ^1_{X_{3}}}A^{3,1}_{1} }{2}\otimes \frac{A^{3,2}_{0}+ (-1)^{\delta ^2_{X_{3}}}A^{3,2}_{1} }{2}\right) \left[ \sum _{k} p_{k}^{(1)} (\rho _{k}^{(11)} \otimes \rho _{k}^{(123)})\right. \\&\quad \left. \left. \otimes \sum _{h} p_{h}^{(2)} (\rho _{h}^{(21)} \otimes \rho _{h}^{(22)}\otimes \rho _{h}^{(23)}) \otimes \sum _{l} p_{l}^{(3)} (\rho _{l}^{(31)} \otimes \rho _{l}^{(32)}\otimes \rho _{l}^{(33)})\right] \right\} \\&= \sum _{k} p_{k}^{(1)} \sum _{h} p_{h}^{(2)} \sum _{l} p_{l}^{(3)} \mathrm {tr} \left[ \left( \frac{A^{1,1}_{0}+ (-1)^{\delta ^1_{X_{1}}}A^{1,1}_{1} }{2} \otimes B_{y_{X}} \otimes C_{z_{X}} \right. \right. \\&\quad \otimes \frac{A^{2,1}_{0}+ (-1)^{\delta ^1_{X_{2}}}A^{2,1}_{1} }{2}\\&\quad \left. \otimes \frac{A^{2,2}_{0}+ (-1)^{\delta ^2_{X_{2}}}A^{2,2}_{1} }{2}\otimes \frac{A^{3,1}_{0}+ (-1)^{\delta ^1_{X_{3}}}A^{3,1}_{1} }{2}\otimes \frac{A^{3,2}_{0}+ (-1)^{\delta ^2_{X_{3}}}A^{3,2}_{1} }{2}\right) \\&\quad \left. \cdot (\rho _{k}^{(11)} \otimes \rho _{k}^{(123)}\otimes \rho _{h}^{(21)} \otimes \rho _{h}^{(22)}\otimes \rho _{h}^{(23)} \otimes \rho _{l}^{(31)} \otimes \rho _{l}^{(32)}\otimes \rho _{l}^{(33)})\right] \\&= \sum _{k} p_{k}^{(1)} \sum _{h} p_{h}^{(2)} \sum _{l} p_{l}^{(3)} \mathrm {tr} \left( \frac{A^{1,1}_{0}+ (-1)^{\delta ^1_{X_{1}}}A^{1,1}_{1} }{2} \rho _{k}^{(11)}\right) \\&\quad \cdot \mathrm {tr} [(B_{y_{X}}\otimes C_{z_{X}}) (\rho _{h}^{(21)}\otimes \rho _{k}^{(123)} \otimes \rho _{l}^{(31)})]\\&\quad \cdot \mathrm {tr} (\frac{A^{2,1}_{0}+ (-1)^{\delta ^1_{X_{2}}}A^{2,1}_{1} }{2} \rho _{h}^{(22)}) \cdot \mathrm {tr} \left( \frac{A^{2,2}_{0}+ (-1)^{\delta ^2_{X_{2}}}A^{2,2}_{1} }{2} \rho _{h}^{(23)}\right) \\&\quad \cdot \mathrm {tr} \left( \frac{A^{3,1}_{0}+ (-1)^{\delta ^1_{X_{3}}}A^{3,1}_{1} }{2} \rho _{l}^{(32)}\right) \cdot \mathrm {tr} \left( \frac{A^{3,2}_{0}+ (-1)^{\delta ^2_{X_{3}}}A^{3,2}_{1} }{2} \rho _{l}^{(33)}\right) . \end{aligned}$$

As $| \mathrm {tr} [(B_{y_{X}}\otimes C_{z_{X}}) (\rho _{h}^{(21)}\otimes \rho _{k}^{(123)} \otimes \rho _{l}^{(31)})]| = |P(0,0|y_X,z_X)- P(0,1|y_X,z_X)- P(1,0|y_X,z_X) + P(1,1|y_X,z_X)| \le 1$ holds for any X, one obtains

$$\begin{aligned} |K_{X}|&\le \sum _{k} p_{k}^{(1)} \sum _{h} p_{h}^{(2)} \sum _{l} p_{l}^{(3)} \left| \mathrm {tr} \left( \frac{A^{1,1}_{0}+ (-1)^{\delta ^1_{X_{1}}}A^{1,1}_{1} }{2} \rho _{k}^{(11)}\right) \right| \\&\quad \cdot |\mathrm {tr} [(B_{y_{X}}\otimes C_{z_{X}}) (\rho _{h}^{(21)}\otimes \rho _{k}^{(123)} \otimes \rho _{l}^{(31)})]|\\&\quad \cdot \left| \mathrm {tr} \left( \frac{A^{2,1}_{0}+ (-1)^{\delta ^1_{X_{2}}}A^{2,1}_{1} }{2} \rho _{h}^{(22)}\right) \right| \cdot \left| \mathrm {tr} \left( \frac{A^{2,2}_{0}+ (-1)^{\delta ^2_{X_{2}}}A^{2,2}_{1} }{2} \rho _{h}^{(23)}\right) \right| \\&\quad \cdot \left| \mathrm {tr} \left( \frac{A^{3,1}_{0}+ (-1)^{\delta ^1_{X_{3}}}A^{3,1}_{1} }{2} \rho _{l}^{(32)}\right) \right| \\&\quad \cdot \left| \mathrm {tr} \left( \frac{A^{3,2}_{0}+ (-1)^{\delta ^2_{X_{3}}}A^{3,2}_{1} }{2} \rho _{l}^{(33)}\right) \right| \\&\le \sum _{k} p_{k}^{(1)} \sum _{h} p_{h}^{(2)} \sum _{l} p_{l}^{(3)} \left| \mathrm {tr} \left( \frac{A^{1,1}_{0}+ (-1)^{\delta ^1_{X_{1}}}A^{1,1}_{1} }{2} \rho _{k}^{(11)}\right) \right| \\&\quad \cdot \left| \mathrm {tr} \left( \frac{A^{2,1}_{0}+ (-1)^{\delta ^1_{X_{2}}}A^{2,1}_{1} }{2} \rho _{h}^{(22)}\right) \right| \\&\quad \cdot \left| \mathrm {tr} \left( \frac{A^{2,2}_{0}+ (-1)^{\delta ^2_{X_{2}}}A^{2,2}_{1} }{2} \rho _{h}^{(23)}\right) \right| \cdot \left| \mathrm {tr} \left( \frac{A^{3,1}_{0}+ (-1)^{\delta ^1_{X_{3}}}A^{3,1}_{1} }{2} \rho _{l}^{(32)}\right) \right| \\&\quad \cdot \left| \mathrm {tr} \left( \frac{A^{3,2}_{0}+ (-1)^{\delta ^2_{X_{3}}}A^{3,2}_{1} }{2} \rho _{l}^{(33)}\right) \right| \\&= \left[ \sum _{k} p_{k}^{(1)} \left| \mathrm {tr} \left( \frac{A^{1,1}_{0}+ (-1)^{\delta ^1_{X_{1}}}A^{1,1}_{1} }{2} \rho _{k}^{(11)}\right) \right| \right] \\&\quad \cdot \left[ \sum _{h} p_{h}^{(2)} \left| \mathrm {tr} \left( \frac{A^{2,1}_{0}+ (-1)^{\delta ^1_{X_{2}}}A^{2,1}_{1} }{2} \rho _{h}^{(22)}\right) \right| \right. \\&\quad \cdot \left. \left| \mathrm {tr} \left( \frac{A^{2,2}_{0}+ (-1)^{\delta ^2_{X_{2}}}A^{2,2}_{1} }{2} \rho _{h}^{(23)}\right) \right| \right] \\&\quad \cdot \left[ \sum _{l} p_{l}^{(3)} \left| \mathrm {tr} \left( \frac{A^{3,1}_{0}+ (-1)^{\delta ^1_{X_{3}}}A^{3,1}_{1} }{2} \rho _{l}^{(32)}\right) \right| \right. \\&\quad \cdot \left. \left| \mathrm {tr} \left( \frac{A^{3,2}_{0}+ (-1)^{\delta ^2_{X_{3}}}A^{3,2}_{1} }{2} \rho _{l}^{(33)}\right) \right| \right] . \end{aligned}$$

Now, by the same discussion as that of Proposition 3, one can show that such states do not violate the inequality (5). $\square$

Appendix C: Quantum violations of three biseparable entangled pure states in network of Fig. 3

Suppose that each source $S_i$ $(i=1,2,3)$ emits biseparable entangled pure state $\rho _i= |\varphi ^{i}\rangle \langle \varphi ^{i}|$. As each state $\rho _i$ $(i=1,2,3)$ has three different bipartitions, the overall state $\rho =\rho _1\otimes \rho _2 \otimes \rho _3$ in the network has 27 different partition combinations. For any one of 27 forms, we can find specific example to violate the inequality (5) by choosing suitable measurements.

According to the different choices of quantum states and measurements, we classify 27 cases into the following six groups.

Group 1

This group contains eight cases as listed in Table 1.

Table 1 Eight specific bipartitions for $\rho _1$, $\rho _2$ and $\rho _3$

Here, we only deal with the case 1:

$$\begin{aligned} \rho _1=|\varphi _{(12|3)}^1\rangle \langle \varphi _{(12|3)}^1|,\quad \rho _2=|\varphi _{(12|3)}^2\rangle \langle \varphi _{(12|3)}^2|,\quad \rho _3=|\varphi _{(12|3)}^3\rangle \langle \varphi _{(12|3)}^3|. \end{aligned}$$

For the other seven cases, the proofs are similar. To do this, let $|\varphi _{(12|3)}^i\rangle =\frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}$ for $i=1,2,3$, and write $\rho _i=\rho ^{(i)}_{12} \otimes \rho ^{(i)}_{3}$, $i=1,2,3$. Assume that the parties $A^{1,1}$, $A^{2,1}$, $A^{2,2}$, $A^{3,1}$, $A^{3,2}$ perform the measurements $\{A^{1,1}_{0}= A^{2,1}_{0}= A^{2,2}_{0}= A^{3,1}_{0}= A^{3,2}_{0}= \frac{\sigma _{z}+ \sigma _{x}}{\sqrt{2}}$, $A^{1,1}_{1} =A^{2,1}_{1}= A^{2,2}_{1}= A^{3,1}_{1}= A^{3,2}_{1}= \frac{\sigma _{z}- \sigma _{x}}{\sqrt{2}}\}$ and parties B, C perform the same measurements $\{\sigma _{z} \otimes \sigma _{z}$, $\sigma _{z} \otimes \sigma _{x}$, $\sigma _{x} \otimes \sigma _{z}$, $\sigma _{x} \otimes \sigma _{x}\}$. With the above states and measurements, Eq. (A3) becomes

$$\begin{aligned} K_{X}&= \mathrm {tr} \left[ \left( \frac{A^{1,1}_{0}+ (-1)^{\delta ^1_{X_{1}}}A^{1,1}_{1} }{2} \otimes B_{y_{X}} \otimes \frac{A^{2,1}_{0}+ (-1)^{\delta ^1_{X_{2}}}A^{2,1}_{1} }{2}\right) (\rho _{12}^{(1)} \otimes \rho _{12}^{(2)})\right] \\&\quad \cdot \mathrm {tr} \left[ \frac{A^{2,2}_{0}+ (-1)^{\delta ^2_{X_{2}}}A^{2,2}_{1} }{2} \rho _{3}^{(2)}\right] \\&\quad \cdot \mathrm {tr} \left[ (C_{z_{X}} \otimes \frac{A^{3,1}_{0}+ (-1)^{\delta ^1_{X_{3}}}A^{3,1}_{1} }{2}) (\rho _{3}^{(1)} \otimes \rho _{12}^{(3)})\right] \\&\quad \cdot \mathrm {tr} \left[ \frac{A^{3,2}_{0}+ (-1)^{\delta ^2_{X_{3}}}A^{3,2}_{1} }{2} \rho _{3}^{(3)}\right] . \end{aligned}$$

Note that $X\in \{\emptyset , \{1\}, \{2\}, \{1,2\}\}$. By choosing $B_{y_{\emptyset }}=\sigma _{z}\otimes \sigma _{z}$ and $C_{z_{\emptyset }}=\sigma _{z}\otimes \sigma _{z}$, one gets

$$\begin{aligned} K_{\emptyset }&= \mathrm {tr} \left[ \left( \frac{A^{1,1}_{0}+ A^{1,1}_{1} }{2} \otimes B_{y_{\emptyset }} \otimes \frac{A^{2,1}_{0}+ A^{2,1}_{1} }{2}\right) (\rho _{12}^{(1)} \otimes \rho _{12}^{(2)})\right] \\&\quad \cdot \mathrm {tr} \left[ \frac{A^{2,2}_{0}+ A^{2,2}_{1} }{2} \rho _{3}^{(2)}\right] \\&\quad \cdot \mathrm {tr} \left[ \left( C_{z_{\emptyset }} \otimes \frac{A^{3,1}_{0}+ A^{3,1}_{1} }{2}\right) (\rho _{3}^{(1)} \otimes \rho _{12}^{(3)})\right] \cdot \mathrm {tr} \left[ \frac{A^{3,2}_{0}+ A^{3,2}_{1} }{2} \rho _{3}^{(3)}\right] \\&= \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}} \otimes \sigma _{z}\otimes \sigma _{z} \otimes \frac{\sigma _{z}}{\sqrt{2}}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{z}}{\sqrt{2}} \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \sigma _{z}\otimes \sigma _{z} \otimes \frac{\sigma _{z}}{\sqrt{2}}\right) \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{z}}{\sqrt{2}} \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] =-\frac{1}{32\sqrt{2}}; \end{aligned}$$

by choosing $B_{y_{\{1\}}}=\sigma _{x}\otimes \sigma _{x}$ and $C_{z_{\{1\}}}=\sigma _{z}\otimes \sigma _{x}$, one has

$$\begin{aligned} K_{\{1\}}&= \mathrm {tr} \left[ \left( \frac{A^{1,1}_{0}- A^{1,1}_{1} }{2} \otimes B_{y_{\{1\}}} \otimes \frac{A^{2,1}_{0}- A^{2,1}_{1} }{2}) (\rho _{12}^{(1)} \otimes \rho _{12}^{(2)}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{A^{2,2}_{0}+ A^{2,2}_{1} }{2} \rho _{3}^{(2)}\right] \\&\quad \cdot \mathrm {tr} \left[ \left( C_{z_{\{1\}}} \otimes \frac{A^{3,1}_{0}- A^{3,1}_{1} }{2}) (\rho _{3}^{(1)} \otimes \rho _{12}^{(3)}\right) \right] \cdot \mathrm {tr} \left[ \frac{A^{3,2}_{0}+ A^{3,2}_{1} }{2} \rho _{3}^{(3)}\right] \\&= \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}} \otimes \sigma _{x}\otimes \sigma _{x} \otimes \frac{\sigma _{x}}{\sqrt{2}}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{z}}{\sqrt{2}} \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \sigma _{z}\otimes \sigma _{x} \otimes \frac{\sigma _{x}}{\sqrt{2}}\right) \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{z}}{\sqrt{2}} \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] =-\frac{1}{32\sqrt{2}}; \end{aligned}$$

by choosing $B_{y_{\{2\}}}=\sigma _{z}\otimes \sigma _{z}$ and $C_{z_{\{2\}}}=\sigma _{x}\otimes \sigma _{z}$, one obtains

$$\begin{aligned} K_{\{2\}}&= \mathrm {tr}\left[ \left( \frac{A^{1,1}_{0}+ A^{1,1}_{1} }{2} \otimes B_{y_{\{2\}}} \otimes \frac{A^{2,1}_{0}+ A^{2,1}_{1} }{2}\right) (\rho _{12}^{(1)} \otimes \rho _{12}^{(2)})\right] \\&\quad \cdot \mathrm {tr} \left[ \frac{A^{2,2}_{0}- A^{2,2}_{1} }{2} \rho _{3}^{(2)}\right] \\&\quad \cdot \mathrm {tr} \left[ \left( C_{z_{\{2\}}} \otimes \frac{A^{3,1}_{0}+ A^{3,1}_{1} }{2}\right) (\rho _{3}^{(1)} \otimes \rho _{12}^{(3)})\right] \cdot \mathrm {tr} \left[ \frac{A^{3,2}_{0}- A^{3,2}_{1} }{2} \rho _{3}^{(3)}\right] \\&= \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}} \otimes \sigma _{z}\otimes \sigma _{z} \otimes \frac{\sigma _{z}}{\sqrt{2}}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{x}}{\sqrt{2}} \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \sigma _{x}\otimes \sigma _{z} \otimes \frac{\sigma _{z}}{\sqrt{2}}\right) \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{x}}{\sqrt{2}} \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] =\frac{3\sqrt{3}}{32\sqrt{2}}; \end{aligned}$$

and by choosing $B_{y_{\{1,2\}}}=\sigma _{x}\otimes \sigma _{x}$, $C_{z_{\{1,2\}}}=\sigma _{x}\otimes \sigma _{x}$, one has

$$\begin{aligned} K_{\{1,2\}}&= \mathrm {tr} \left[ \left( \frac{A^{1,1}_{0}- A^{1,1}_{1} }{2} \otimes B_{y_{\{1,2\}}} \otimes \frac{A^{2,1}_{0}- A^{2,1}_{1} }{2}\right) (\rho _{12}^{(1)} \otimes \rho _{12}^{(2)})\right] \\&\quad \cdot \mathrm {tr} \left[ \frac{A^{2,2}_{0}- A^{2,2}_{1} }{2} \rho _{3}^{(2)}\right] \\&\quad \cdot \mathrm {tr} \left[ \left( C_{z_{\{1,2\}}} \otimes \frac{A^{3,1}_{0}- A^{3,1}_{1} }{2}\right) (\rho _{3}^{(1)} \otimes \rho _{12}^{(3)})\right] \cdot \mathrm {tr} \left[ \frac{A^{3,2}_{0}- A^{3,2}_{1} }{2} \rho _{3}^{(3)}\right] \\&= \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}} \otimes \sigma _{x}\otimes \sigma _{x} \otimes \frac{\sigma _{x}}{\sqrt{2}}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{x}}{\sqrt{2}} \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \sigma _{x}\otimes \sigma _{x} \otimes \frac{\sigma _{x}}{\sqrt{2}}\right) \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{x}}{\sqrt{2}} \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] =\frac{3\sqrt{3}}{32\sqrt{2}}. \end{aligned}$$

Thus,

$$\begin{aligned} \sum \limits _{X\in \mathbb {P}(\mathbb {N}_{L})}|K_{X}|^{\frac{1}{3}}&= |K_{\emptyset }|^{\frac{1}{3}}+ |K_{\{1\}}|^{\frac{1}{3}}+ |K_{\{2\}}|^{\frac{1}{3}}+ |K_{\{1,2\}}|^{\frac{1}{3}}\\&= \left| -\frac{1}{32\sqrt{2}}\right| ^{\frac{1}{3}}+ \left| -\frac{1}{32\sqrt{2}}\right| ^{\frac{1}{3}}+ \left| \frac{3\sqrt{3}}{32\sqrt{2}}\right| ^{\frac{1}{3}}+ \left| \frac{3\sqrt{3}}{32\sqrt{2}}\right| ^{\frac{1}{3}}\\&= \frac{1}{\root 6 \of {32}} (1+\sqrt{3})> 2^{\frac{1}{3}}, \end{aligned}$$

violating the 3-local inequality (5).

Group 2

This group contains eight cases as listed in Table 2.

Table 2 Eight specific bipartitions for $\rho _1$, $\rho _2$ and $\rho _3$

Still, we only discuss the case 1:

$$\begin{aligned} \rho _1=|\varphi _{(12|3)}^1\rangle \langle \varphi _{(12|3)}^1|,\quad \rho _2=|\varphi _{(12|3)}^2\rangle \langle \varphi _{(12|3)}^2|,\quad \rho _3=|\varphi _{(23|1)}^3\rangle \langle \varphi _{(23|1)}^3|. \end{aligned}$$

Take $|\varphi _{(12|3)}^1\rangle = |\varphi _{(12|3)}^2\rangle =\frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}$ and $|\varphi _{(23|1)}^3\rangle = \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}$. Write $\rho _1=\rho ^{(1)}_{12} \otimes \rho ^{(1)}_{3}$, $\rho _2=\rho ^{(2)}_{12} \otimes \rho ^{(2)}_{3}$ and $\rho _3=\rho ^{(3)}_{1} \otimes \rho ^{(3)}_{23}$. Assume the parties $A^{1,1}$, $A^{2,1}$, $A^{2,2}$, $A^{3,1}$ perform the measurements $A^{1,1}_{0}= A^{2,1}_{0}= A^{2,2}_{0}= A^{3,1}_{0}=\frac{\sigma _{z}+ \sigma _{x}}{\sqrt{2}}$ and $A^{1,1}_{1} = A^{2,1}_{1}= A^{2,2}_{1}= A^{3,1}_{1}= \frac{\sigma _{z}- \sigma _{x}}{\sqrt{2}}$, while the party $A^{3,2}$ performs the measurements $A^{3,2}_{0}= \sigma _{z}$ and $A^{3,2}_{1}= \sigma _{x}$. For parties B and C, their measurement choices are $\{\sigma _{z} \otimes \sigma _{z}$, $\sigma _{z} \otimes \sigma _{x}$, $\sigma _{x} \otimes \sigma _{z}$, $\sigma _{x} \otimes \sigma _{x}\}$.

In this circumstance, Eq. (A3) becomes

$$\begin{aligned} K_{X}= & {} \mathrm {tr} \left[ \left( \frac{A^{1,1}_{0}+ (-1)^{\delta ^1_{X_{1}}}A^{1,1}_{1} }{2} \otimes B_{y_{X}} \otimes \frac{A^{2,1}_{0}+ (-1)^{\delta ^1_{X_{2}}}A^{2,1}_{1} }{2}\right) (\rho _{12}^{(1)} \otimes \rho _{12}^{(2)})\right] \\&\cdot \mathrm {tr} \left[ \frac{A^{2,2}_{0}+ (-1)^{\delta ^2_{X_{2}}}A^{2,2}_{1} }{2} \rho _{3}^{(2)}\right] \\&\cdot \mathrm {tr} [C_{z_{X}} ( \rho _{3}^{(1)} \otimes \rho _{1}^{(3)})]\\&\cdot \mathrm {tr} \left[ \left( \frac{A^{3,1}_{0}+ (-1)^{\delta ^1_{X_{3}}}A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}+ (-1)^{\delta ^2_{X_{3}}}A^{3,2}_{1} }{2}\right) \rho _{23}^{(3)}\right] . \end{aligned}$$

Letting $B_{y_{\emptyset }}=\sigma _{z}\otimes \sigma _{z}$ and $C_{z_{\emptyset }}=\sigma _{z}\otimes \sigma _{z}$; and then

$$\begin{aligned} K_{\emptyset }= & {} \mathrm {tr} \left[ \left( \frac{A^{1,1}_{0}+ A^{1,1}_{1} }{2} \otimes B_{y_{\emptyset }} \otimes \frac{A^{2,1}_{0}+ A^{2,1}_{1} }{2}\right) (\rho _{12}^{(1)} \otimes \rho _{12}^{(2)})\right] \\&\cdot \mathrm {tr} \left[ \frac{A^{2,2}_{0}+ A^{2,2}_{1} }{2} \rho _{3}^{(2)}\right] \\&\cdot \mathrm {tr} [C_{z_{\emptyset }} ( \rho _{3}^{(1)} \otimes \rho _{1}^{(3)})]\\&\cdot \mathrm {tr} \left[ \left( \frac{A^{3,1}_{0}+ A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}+ A^{3,2}_{1} }{2}\right) \rho _{23}^{(3)}\right] \\= & {} \mathrm {tr}\left[ \left( \frac{\sigma _{z}}{\sqrt{2}} \otimes \sigma _{z}\otimes \sigma _{z} \otimes \frac{\sigma _{z}}{\sqrt{2}}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\cdot \mathrm {tr} \left[ \frac{\sigma _{z}}{\sqrt{2}} \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] \\&\cdot \mathrm {tr} \left[ (\sigma _{z}\otimes \sigma _{z} ) \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] \\&\cdot \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}} \otimes \frac{\sigma _{z}+ \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] =-\frac{1}{64}. \end{aligned}$$

Letting $B_{y_{\{1\}}}=\sigma _{x}\otimes \sigma _{x}$ and $C_{z_{\{1\}}}=\sigma _{z}\otimes \sigma _{x}$, and then

$$\begin{aligned} K_{\{1\}}&= \mathrm {tr} \left[ \left( \frac{A^{1,1}_{0}- A^{1,1}_{1} }{2} \otimes B_{y_{\{1\}}} \otimes \frac{A^{2,1}_{0}- A^{2,1}_{1} }{2}\right) (\rho _{12}^{(1)} \otimes \rho _{12}^{(2)})\right] \\&\quad \cdot \mathrm {tr} \left[ \frac{A^{2,2}_{0}+ A^{2,2}_{1} }{2} \rho _{3}^{(2)}\right] \\&\quad \cdot \mathrm {tr} [C_{z_{\{1\}}} ( \rho _{3}^{(1)} \otimes \rho _{1}^{(3)})]\\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{3,1}_{0}- A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}+ A^{3,2}_{1} }{2}\right) \rho _{23}^{(3)}\right] \\&= \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}} \otimes \sigma _{x}\otimes \sigma _{x} \otimes \frac{\sigma _{x}}{\sqrt{2}}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{z}}{\sqrt{2}} \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ (\sigma _{z}\otimes \sigma _{x} ) \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}} \otimes \frac{\sigma _{z}+ \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] =\frac{\sqrt{3}}{64}. \end{aligned}$$

Letting $B_{y_{\{2\}}}=\sigma _{z}\otimes \sigma _{z}$ and $C_{z_{\{2\}}}=\sigma _{x}\otimes \sigma _{z}$, we get

$$\begin{aligned} K_{\{2\}}&= \mathrm {tr} \left[ \left( \frac{A^{1,1}_{0}+ A^{1,1}_{1} }{2} \otimes B_{y_{\{2\}}} \otimes \frac{A^{2,1}_{0}+ A^{2,1}_{1} }{2}\right) (\rho _{12}^{(1)} \otimes \rho _{12}^{(2)})\right] \\&\quad \cdot \mathrm {tr} \left[ \frac{A^{2,2}_{0}- A^{2,2}_{1} }{2} \rho _{3}^{(2)}\right] \\&\quad \cdot \mathrm {tr} [C_{z_{\{2\}}} ( \rho _{3}^{(1)} \otimes \rho _{1}^{(3)})]\\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{3,1}_{0}+ A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}- A^{3,2}_{1} }{2}\right) \rho _{23}^{(3)}\right] \\&= \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}} \otimes \sigma _{z}\otimes \sigma _{z} \otimes \frac{\sigma _{z}}{\sqrt{2}}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{x}}{\sqrt{2}} \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ (\sigma _{x}\otimes \sigma _{z} ) \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}} \otimes \frac{\sigma _{z}- \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] = -\frac{3}{64}. \end{aligned}$$

Letting $B_{y_{\{1,2\}}}=\sigma _{x}\otimes \sigma _{x}$ and $C_{z_{\{1,2\}}}=\sigma _{x}\otimes \sigma _{x}$, one has

$$\begin{aligned} K_{\{1,2\}}&= \mathrm {tr} \left[ \left( \frac{A^{1,1}_{0}- A^{1,1}_{1} }{2} \otimes B_{y_{\{1,2\}}} \otimes \frac{A^{2,1}_{0}- A^{2,1}_{1} }{2}\right) (\rho _{12}^{(1)} \otimes \rho _{12}^{(2)})\right] \\&\quad \cdot \mathrm {tr} \left[ \frac{A^{2,2}_{0}- A^{2,2}_{1} }{2} \rho _{3}^{(2)}\right] \\&\quad \cdot \mathrm {tr} [C_{z_{\{1,2\}}} ( \rho _{3}^{(1)} \otimes \rho _{1}^{(3)})]\\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{3,1}_{0}- A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}- A^{3,2}_{1} }{2}\right) \rho _{23}^{(3)}\right] \\&= \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}} \otimes \sigma _{x}\otimes \sigma _{x} \otimes \frac{\sigma _{x}}{\sqrt{2}}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{x}}{\sqrt{2}} \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ (\sigma _{x}\otimes \sigma _{x} ) \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}} \otimes \frac{\sigma _{z}- \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] =-\frac{3\sqrt{3}}{64}. \end{aligned}$$

Thus,

$$\begin{aligned} \sum \limits _{X\in \mathbb {P}(\mathbb {N}_{L})}|K_{X}|^{\frac{1}{3}}&= |K_{\emptyset }|^{\frac{1}{3}}+ |K_{\{1\}}|^{\frac{1}{3}}+ |K_{\{2\}}|^{\frac{1}{3}}+ |K_{\{1,2\}}|^{\frac{1}{3}}\\&= \left| -\frac{1}{64}\right| ^{\frac{1}{3}}+ \left| \frac{\sqrt{3}}{64}\right| ^{\frac{1}{3}}+ \left| -\frac{3}{64}\right| ^{\frac{1}{3}}+ \left| -\frac{3\sqrt{3}}{64}\right| ^{\frac{1}{3}}\\&= \frac{1}{4}(1+ \root 6 \of {3}+ \root 3 \of {3}+ \sqrt{3})> 2^{\frac{1}{3}}, \end{aligned}$$

violating the 3-local inequality (5).

Group 3

This group contains two cases as listed in Table 3.

Table 3 Two specific bipartitions for $\rho _1$, $\rho _2$ and $\rho _3$

We exemplify the case 1:

$$\begin{aligned} \rho _1=|\varphi _{(12|3)}^1\rangle \langle \varphi _{(12|3)}^1|,\quad \rho _2=|\varphi _{(23|1)}^2\rangle \langle \varphi _{(23|1)}^2|,\quad \rho _3=|\varphi _{(23|1)}^3\rangle \langle \varphi _{(23|1)}^3|. \end{aligned}$$

In this circumstance, take $|\varphi _{(12|3)}^1\rangle =\frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}$ and $|\varphi _{(23|1)}^2\rangle = |\varphi _{(23|1)}^3\rangle = \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}$. Write $\rho _1=\rho ^{(1)}_{12} \otimes \rho ^{(1)}_{3}$, $\rho _2=\rho ^{(2)}_{1} \otimes \rho ^{(2)}_{23}$ and $\rho _3=\rho ^{(3)}_{1} \otimes \rho ^{(3)}_{23}$. Let the parties $A^{1,1}$, $A^{2,1}$, $A^{3,1}$ perform the measurements $A^{1,1}_{0}= A^{2,1}_{0}= A^{3,1}_{0}=\frac{\sigma _{z}+ \sigma _{x}}{\sqrt{2}}$ and $A^{1,1}_{1} = A^{2,1}_{1}= A^{3,1}_{1}= \frac{\sigma _{z}- \sigma _{x}}{\sqrt{2}}$, while the parties $A^{2,2}$, $A^{3,2}$ perform the measurements $A^{2,2}_{0}= A^{3,2}_{0}= \sigma _{z}$ and $A^{2,2}_{1}=A^{3,2}_{1}= \sigma _{x}$. Assume that the measurement choices of parties B and C are $\{\sigma _{z} \otimes \sigma _{z}$, $\sigma _{z} \otimes \sigma _{x}$, $\sigma _{x} \otimes \sigma _{z}$, $\sigma _{x} \otimes \sigma _{x}\}$, respectively. Thus, Eq. (A3) reduces to

$$\begin{aligned} K_{X}&= \mathrm {tr} \left[ \left( \frac{A^{1,1}_{0}+ (-1)^{\delta ^1_{X_{1}}}A^{1,1}_{1} }{2} \otimes B_{y_{X}} \right) (\rho _{12}^{(1)} \otimes \rho _{1}^{(2)})\right] \cdot \mathrm {tr} [C_{z_{X}} ( \rho _{3}^{(1)} \otimes \rho _{1}^{(3)})]\\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{2,1}_{0}+ (-1)^{\delta ^1_{X_{2}}}A^{2,1}_{1} }{2}\otimes \frac{A^{2,2}_{0}+ (-1)^{\delta ^2_{X_{2}}}A^{2,2}_{1} }{2}\right) \rho _{23}^{(2)}\right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{3,1}_{0}+ (-1)^{\delta ^1_{X_{3}}}A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}+ (-1)^{\delta ^2_{X_{3}}}A^{3,2}_{1} }{2}\right) \rho _{23}^{(3)}\right] . \end{aligned}$$

By taking $B_{y_{\emptyset }}=\sigma _{z}\otimes \sigma _{z}$ and $C_{z_{\emptyset }}=\sigma _{z}\otimes \sigma _{z}$, $B_{y_{\{1\}}}=\sigma _{x}\otimes \sigma _{x}$ and $C_{z_{\{1\}}}=\sigma _{x}\otimes \sigma _{x}$, $B_{y_{\{2\}}}=\sigma _{z}\otimes \sigma _{x}$ (or $\sigma _{x}\otimes \sigma _{z}$) and $C_{z_{\{2\}}}=\sigma _{z}\otimes \sigma _{x}$ (or $\sigma _{x}\otimes \sigma _{z}$), $B_{y_{\{1,2\}}}=\sigma _{x}\otimes \sigma _{x}$ and $C_{z_{\{1,2\}}}=\sigma _{x}\otimes \sigma _{x}$, respectively, one can obtain

$$\begin{aligned} K_{\emptyset }&= \mathrm {tr} \left[ \left( \frac{A^{1,1}_{0}+ A^{1,1}_{1} }{2} \otimes B_{y_{\emptyset }} \right) (\rho _{12}^{(1)} \otimes \rho _{1}^{(2)})\right] \cdot \mathrm {tr} [C_{z_{\emptyset }} ( \rho _{3}^{(1)} \otimes \rho _{1}^{(3)})]\\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{2,1}_{0}+ A^{2,1}_{1} }{2}\otimes \frac{A^{2,2}_{0}+ A^{2,2}_{1} }{2}\right) \rho _{23}^{(2)}\right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{3,1}_{0}+ A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}+ A^{3,2}_{1} }{2}\right) \rho _{23}^{(3)}\right] \\&= \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}} \otimes \sigma _{z}\otimes \sigma _{z}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ (\sigma _{z}\otimes \sigma _{z}) \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}} \otimes \frac{\sigma _{z}+ \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}} \otimes \frac{\sigma _{z}+ \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] =-\frac{1}{64\sqrt{2}}, \end{aligned}$$

$$\begin{aligned} K_{\{1\}}&= \mathrm {tr} \left[ \left( \frac{A^{1,1}_{0}- A^{1,1}_{1} }{2}\otimes B_{y_{\{1\}}} \right) (\rho _{12}^{(1)} \otimes \rho _{1}^{(2)})\right] \cdot \mathrm {tr} [C_{z_{\{1\}}} ( \rho _{3}^{(1)} \otimes \rho _{1}^{(3)})]\\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{2,1}_{0}- A^{2,1}_{1} }{2}\otimes \frac{A^{2,2}_{0}+ A^{2,2}_{1} }{2}\right) \rho _{23}^{(2)}\right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{3,1}_{0}- A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}+ A^{3,2}_{1} }{2}\right) \rho _{23}^{(3)}\right] \\&= \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}} \otimes \sigma _{x}\otimes \sigma _{x}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ (\sigma _{x}\otimes \sigma _{x}) \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}} \otimes \frac{\sigma _{z}+ \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}} \otimes \frac{\sigma _{z}+ \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] =\frac{3\sqrt{3}}{64\sqrt{2}}, \end{aligned}$$

$$\begin{aligned} K_{\{2\}}&= \mathrm {tr} \left[ \left( \frac{A^{1,1}_{0}+ A^{1,1}_{1} }{2}\otimes B_{y_{\{2\}}} \right) (\rho _{12}^{(1)} \otimes \rho _{1}^{(2)})\right] \cdot \mathrm {tr} [C_{z_{\{2\}}} ( \rho _{3}^{(1)} \otimes \rho _{1}^{(3)})]\\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{2,1}_{0}+ A^{2,1}_{1} }{2}\otimes \frac{A^{2,2}_{0}- A^{2,2}_{1} }{2}\right) \rho _{23}^{(2)}\right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{3,1}_{0}+ A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}- A^{3,2}_{1} }{2}\right) \rho _{23}^{(3)}\right] \\&= \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}} \otimes \sigma _{z}\otimes \sigma _{x}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ (\sigma _{z}\otimes \sigma _{x}) \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}} \otimes \frac{\sigma _{z}- \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}} \otimes \frac{\sigma _{z}- \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] -\frac{3}{64\sqrt{2}} \end{aligned}$$

and

$$\begin{aligned} K_{\{1,2\}}&= \mathrm {tr} \left[ \left( \frac{A^{1,1}_{0}- A^{1,1}_{1} }{2}\otimes B_{y_{\{1,2\}}} \right) (\rho _{12}^{(1)} \otimes \rho _{1}^{(2)})\right] \cdot \mathrm {tr} [C_{z_{\{1,2\}}} ( \rho _{3}^{(1)} \otimes \rho _{1}^{(3)})]\\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{2,1}_{0}- A^{2,1}_{1} }{2}\otimes \frac{A^{2,2}_{0}- A^{2,2}_{1} }{2}\right) \rho _{23}^{(2)}\right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{3,1}_{0}- A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}- A^{3,2}_{1} }{2}\right) \rho _{23}^{(3)}\right] \\&= \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}} \otimes \sigma _{x}\otimes \sigma _{x}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ (\sigma _{x}\otimes \sigma _{x}) \left( \frac{|0\rangle +\sqrt{3}|1\rangle }{2} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}} \otimes \frac{\sigma _{z}- \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}} \otimes \frac{\sigma _{z}- \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] =\frac{3\sqrt{3}}{64\sqrt{2}}. \end{aligned}$$

Hence,

$$\begin{aligned} \sum \limits _{X\in \mathbb {P}(\mathbb {N}_{L})}|K_{X}|^{\frac{1}{3}}&= |K_{\emptyset }|^{\frac{1}{3}}+ |K_{\{1\}}|^{\frac{1}{3}}+ |K_{\{2\}}|^{\frac{1}{3}}+ |K_{\{1,2\}}|^{\frac{1}{3}}\\&= \left| -\frac{1}{64\sqrt{2}}\right| ^{\frac{1}{3}}+ \left| \frac{3\sqrt{3}}{64\sqrt{2}}\right| ^{\frac{1}{3}}+ \left| -\frac{3}{64\sqrt{2}}\right| ^{\frac{1}{3}}+ \left| \frac{3\sqrt{3}}{64\sqrt{2}}\right| ^{\frac{1}{3}}\\&= \frac{1}{2\root 6 \of {2}}(1+2 \sqrt{3}+ \root 3 \of {3})> 2^{\frac{1}{3}}, \end{aligned}$$

violating the 3-local inequality (5).

Group 4

This group contains four cases as listed in Table 4.

Table 4 Four specific bipartitions for $\rho _1$, $\rho _2$ and $\rho _3$

For example, for the case 1:

$$\begin{aligned} \rho _1=|\varphi _{(23|1)}^1\rangle \langle \varphi _{(23|1)}^1|,\quad \rho _2=|\varphi _{(12|3)}^2\rangle \langle \varphi _{(12|3)}^2|, \quad \rho _3=|\varphi _{(12|3)}^3\rangle \langle \varphi _{(12|3)}^3|, \end{aligned}$$

we take $|\varphi _{(23|1)}^1\rangle = \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}$ and $|\varphi _{(12|3)}^2\rangle = |\varphi _{(12|3)}^3\rangle = \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}$. Write $\rho _1=\rho ^{(1)}_{1} \otimes \rho ^{(1)}_{23}$, $\rho _2=\rho ^{(2)}_{12} \otimes \rho ^{(2)}_{3}$ and $\rho _3=\rho ^{(3)}_{12} \otimes \rho ^{(3)}_{3}$. Assume that the parties $A^{1,1}$, $A^{2,1}$, $A^{2,2}$, $A^{3,1}$, $A^{3,2}$ perform the measurements $A^{1,1}_{0}= A^{2,1}_{0}= A^{2,2}_{0}=A^{3,1}_{0}=A^{3,2}_{0}=\frac{\sigma _{z}+ \sigma _{x}}{\sqrt{2}}$ and $A^{1,1}_{1} = A^{2,1}_{1}=A^{2,2}_{1}= A^{3,1}_{1}=A^{3,2}_{1}= \frac{\sigma _{z}- \sigma _{x}}{\sqrt{2}}$, and parties B, C perform the measurements $\{\sigma _{z} \otimes \sigma _{z}$, $\sigma _{z} \otimes \sigma _{x}$, $\sigma _{x} \otimes \sigma _{z}$, $\sigma _{x} \otimes \sigma _{x}\}$, respectively. Then, Eq. (A3) becomes

$$\begin{aligned} K_{X}&= \mathrm {tr} \left[ \left( \frac{A^{2,1}_{0}+ (-1)^{\delta ^1_{X_{2}}}A^{2,1}_{1} }{2}\otimes B_{y_{X}}\otimes C_{z_{X}}\right. \right. \\&\quad \left. \left. \otimes \frac{A^{3,1}_{0}+ (-1)^{\delta ^1_{X_{3}}}A^{3,1}_{1} }{2}\right) (\rho _{12}^{(2)}\otimes \rho _{23}^{(1)}\otimes \rho _{12}^{(3)})\right] \\&\quad \cdot \mathrm {tr} \left[ \frac{A^{1,1}_{0}+ (-1)^{\delta ^1_{X_{1}}}A^{1,1}_{1} }{2}\rho _{1}^{(1)}\right] \cdot \mathrm {tr} \left[ \frac{A^{2,2}_{0}+ (-1)^{\delta ^2_{X_{2}}}A^{2,2}_{1} }{2} \rho _{3}^{(2)}\right] \\&\quad \cdot \mathrm {tr} \left[ \frac{A^{3,2}_{0}+ (-1)^{\delta ^2_{X_{3}}}A^{3,2}_{1} }{2} \rho _{3}^{(3)}\right] . \end{aligned}$$

By choosing $B_{y_{\emptyset }}=\sigma _{z}\otimes \sigma _{z}$ and $C_{z_{\emptyset }}=\sigma _{z}\otimes \sigma _{z}$, $B_{y_{\{1\}}}=\sigma _{x}\otimes \sigma _{z}$ and $C_{z_{\{1\}}}=\sigma _{z}\otimes \sigma _{x}$, $B_{y_{\{2\}}}=\sigma _{z}\otimes \sigma _{x}$ and $C_{z_{\{2\}}}=\sigma _{x}\otimes \sigma _{z}$, $B_{y_{\{1,2\}}}=\sigma _{x}\otimes \sigma _{x}$ and $C_{z_{\{1,2\}}}=\sigma _{x}\otimes \sigma _{x}$, respectively, one gets

$$\begin{aligned} K_{\emptyset }&= \mathrm {tr} \left[ \left( \frac{A^{2,1}_{0}+ A^{2,1}_{1} }{2}\otimes B_{y_{\emptyset }}\otimes C_{z_{\emptyset }} \otimes \frac{A^{3,1}_{0}+ A^{3,1}_{1} }{2}\right) (\rho _{12}^{(2)}\otimes \rho _{23}^{(1)}\otimes \rho _{12}^{(3)})\right] \\&\quad \cdot \mathrm {tr} \left[ \frac{A^{1,1}_{0}+ A^{1,1}_{1} }{2}\rho _{1}^{(1)}\right] \cdot \mathrm {tr} \left[ \frac{A^{2,2}_{0}+ A^{2,2}_{1} }{2} \rho _{3}^{(2)}\right] \cdot \mathrm {tr} \left[ \frac{A^{3,2}_{0}+ A^{3,2}_{1} }{2} \rho _{3}^{(3)}\right] \\&= \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}} \otimes \sigma _{z}\otimes \sigma _{z}\otimes \sigma _{z}\otimes \sigma _{z}\otimes \frac{\sigma _{z}}{\sqrt{2}}\right) \right. \\&\quad \cdot \left. \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{z}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] \cdot \mathrm {tr} \left[ \frac{\sigma _{z}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{z}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] =-\frac{1}{32\sqrt{2}}, \end{aligned}$$

$$\begin{aligned} K_{\{1\}}&= \mathrm {tr} \left[ \left( \frac{A^{2,1}_{0}- A^{2,1}_{1} }{2}\otimes B_{y_{\{1\}}}\otimes C_{z_{\{1\}}} \otimes \frac{A^{3,1}_{0}- A^{3,1}_{1} }{2}\right) (\rho _{12}^{(2)}\otimes \rho _{23}^{(1)}\otimes \rho _{12}^{(3)})\right] \\&\quad \cdot \mathrm {tr} \left[ \frac{A^{1,1}_{0}- A^{1,1}_{1} }{2}\rho _{1}^{(1)}\right] \cdot \mathrm {tr} \left[ \frac{A^{2,2}_{0}+ A^{2,2}_{1} }{2} \rho _{3}^{(2)}\right] \cdot \mathrm {tr} \left[ \frac{A^{3,2}_{0}+ A^{3,2}_{1} }{2} \rho _{3}^{(3)}\right] \\&= \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}} \otimes \sigma _{x}\otimes \sigma _{z}\otimes \sigma _{z}\otimes \sigma _{x}\otimes \frac{\sigma _{x}}{\sqrt{2}}\right) \right. \\&\quad \cdot \left. \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{x}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] \cdot \mathrm {tr} \left[ \frac{\sigma _{z}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{z}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] =\frac{\sqrt{3}}{32\sqrt{2}}, \end{aligned}$$

$$\begin{aligned} K_{\{2\}}&= \mathrm {tr} \left[ \left( \frac{A^{2,1}_{0}+ A^{2,1}_{1} }{2}\otimes B_{y_{\{2\}}}\otimes C_{z_{\{2\}}} \otimes \frac{A^{3,1}_{0}+ A^{3,1}_{1} }{2}\right) (\rho _{12}^{(2)}\otimes \rho _{23}^{(1)}\otimes \rho _{12}^{(3)})\right] \\&\quad \cdot \mathrm {tr} \left[ \frac{A^{1,1}_{0}+ A^{1,1}_{1} }{2}\rho _{1}^{(1)}\right] \cdot \mathrm {tr} \left[ \frac{A^{2,2}_{0}- A^{2,2}_{1} }{2} \rho _{3}^{(2)}\right] \cdot \mathrm {tr} \left[ \frac{A^{3,2}_{0}- A^{3,2}_{1} }{2} \rho _{3}^{(3)}\right] \\&= \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}} \otimes \sigma _{z}\otimes \sigma _{x}\otimes \sigma _{x}\otimes \sigma _{z}\otimes \frac{\sigma _{z}}{\sqrt{2}}\right) \right. \\&\quad \left. \cdot \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{z}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] \cdot \mathrm {tr} \left[ \frac{\sigma _{x}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{x}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] = -\frac{3}{32\sqrt{2}} \end{aligned}$$

and

$$\begin{aligned} K_{\{1,2\}}&\!=\! \mathrm {tr} \left[ \left( \frac{A^{2,1}_{0}- A^{2,1}_{1} }{2}\otimes B_{y_{\{1,2\}}}\otimes C_{z_{\{1,2\}}} \otimes \frac{A^{3,1}_{0}- A^{3,1}_{1} }{2}\right) (\rho _{12}^{(2)}\otimes \rho _{23}^{(1)}\otimes \rho _{12}^{(3)})\right] \\&\quad \cdot \mathrm {tr} \left[ \frac{A^{1,1}_{0}- A^{1,1}_{1} }{2}\rho _{1}^{(1)}\right] \cdot \mathrm {tr} \left[ \frac{A^{2,2}_{0}- A^{2,2}_{1} }{2} \rho _{3}^{(2)}\right] \cdot \mathrm {tr} \left[ \frac{A^{3,2}_{0}- A^{3,2}_{1} }{2} \rho _{3}^{(3)}\right] \\&= \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}} \otimes \sigma _{x}\otimes \sigma _{x}\otimes \sigma _{x}\otimes \sigma _{x}\otimes \frac{\sigma _{x}}{\sqrt{2}}\right) \right. \\&\quad \left. \cdot \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{x}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] \cdot \mathrm {tr} \left[ \frac{\sigma _{x}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{x}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] = \frac{3\sqrt{3}}{32\sqrt{2}}. \end{aligned}$$

It follows that

$$\begin{aligned} \sum \limits _{X\in \mathbb {P}(\mathbb {N}_{L})}|K_{X}|^{\frac{1}{3}}&= |K_{\emptyset }|^{\frac{1}{3}}+ |K_{\{1\}}|^{\frac{1}{3}}+ |K_{\{2\}}|^{\frac{1}{3}}+ |K_{\{1,2\}}|^{\frac{1}{3}}\\&= \left| -\frac{1}{32\sqrt{2}}\right| ^{\frac{1}{3}}+ \left| \frac{\sqrt{3}}{32\sqrt{2}}\right| ^{\frac{1}{3}}+ \left| -\frac{3}{32\sqrt{2}}\right| ^{\frac{1}{3}}+ \left| \frac{3\sqrt{3}}{32\sqrt{2}}\right| ^{\frac{1}{3}}\\&= \frac{1}{2\root 6 \of {32}} (1+ \root 6 \of {3}+ \root 3 \of {3}+ \sqrt{3})> 2^{\frac{1}{3}}, \end{aligned}$$

violating the 3-local inequality (5).

Group 5

This group contains four cases as listed in Table 5.

Table 5 Four specific bipartitions for $\rho _1$, $\rho _2$ and $\rho _3$

Consider the case 1:

$$\begin{aligned} \rho _1=|\varphi _{(23|1)}^1\rangle \langle \varphi _{(23|1)}^1|,\quad \rho _2=|\varphi _{(12|3)}^2\rangle \langle \varphi _{(12|3)}^2|, \quad \rho _3=|\varphi _{(23|1)}^3\rangle \langle \varphi _{(23|1)}^3|, \end{aligned}$$

take $|\varphi _{(23|1)}^1\rangle = |\varphi _{(23|1)}^3\rangle =\frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}$ and $|\varphi _{(12|3)}^2\rangle =\frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}$. Let $\rho _1=\rho ^{(1)}_{1} \otimes \rho ^{(1)}_{23}$, $\rho _2=\rho ^{(2)}_{12} \otimes \rho ^{(2)}_{3}$ and $\rho _3=\rho ^{(3)}_{1} \otimes \rho ^{(3)}_{23}$. Assume the parties $A^{1,1}$, $A^{2,1}$, $A^{2,2}$, $A^{3,1}$ perform the measurements $A^{1,1}_{0}= A^{2,1}_{0}= A^{2,2}_{0}=A^{3,1}_{0}=\frac{\sigma _{z}+ \sigma _{x}}{\sqrt{2}}$ and $A^{1,1}_{1} = A^{2,1}_{1}=A^{2,2}_{1}= A^{3,1}_{1}=\frac{\sigma _{z}- \sigma _{x}}{\sqrt{2}}$, while the party $A^{3,2}$ performs the measurements $A^{3,2}_{0}=\sigma _{z}$ and $A^{3,2}_{1}=\sigma _{x}$. The measurement choices of parties B and C are $\{\sigma _{z} \otimes \sigma _{z}$, $\sigma _{z} \otimes \sigma _{x}$, $\sigma _{x} \otimes \sigma _{z}$, $\sigma _{x} \otimes \sigma _{x}\}$, respectively.

In this circumstance, Eq. (A3) reduces to

$$\begin{aligned} K_{X}&= \mathrm {tr} \left[ \frac{A^{1,1}_{0}+ (-1)^{\delta ^1_{X_{1}}}A^{1,1}_{1} }{2}\rho _{1}^{(1)}\right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{2,1}_{0}+ (-1)^{\delta ^1_{X_{2}}}A^{2,1}_{1} }{2}\otimes B_{y_{X}}\otimes C_{z_{X}}\right) (\rho _{12}^{(2)}\otimes \rho _{23}^{(1)}\otimes \rho _{1}^{(3)})\right] \\&\quad \cdot \mathrm {tr} \left[ \frac{A^{2,2}_{0}+ (-1)^{\delta ^2_{X_{2}}}A^{2,2}_{1} }{2} \rho _{3}^{(2)}\right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{3,1}_{0}+ (-1)^{\delta ^1_{X_{3}}}A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}+ (-1)^{\delta ^2_{X_{3}}}A^{3,2}_{1} }{2}\right) \rho _{23}^{(3)}\right] . \end{aligned}$$

Choose $B_{y_{\emptyset }}=\sigma _{z}\otimes \sigma _{z}$ and $C_{z_{\emptyset }}=\sigma _{z}\otimes \sigma _{z}$, $B_{y_{\{1\}}}=\sigma _{x}\otimes \sigma _{z}$ and $C_{z_{\{1\}}}=\sigma _{z}\otimes \sigma _{x}$, $B_{y_{\{2\}}}=\sigma _{z}\otimes \sigma _{x}$ and $C_{z_{\{2\}}}=\sigma _{x}\otimes \sigma _{z}$, $B_{y_{\{1,2\}}}=\sigma _{x}\otimes \sigma _{x}$ and $C_{z_{\{1,2\}}}=\sigma _{x}\otimes \sigma _{x}$, respectively; then

$$\begin{aligned} K_{\emptyset }&=\! \mathrm {tr}\! \left[ \frac{A^{1,1}_{0}+ A^{1,1}_{1} }{2}\rho _{1}^{(1)}\right] \! \cdot \mathrm {tr} \left[ \left( \frac{A^{2,1}_{0}+ A^{2,1}_{1} }{2}\otimes B_{y_{\emptyset }}\otimes C_{z_{\emptyset }}\right) (\rho _{12}^{(2)}\otimes \rho _{23}^{(1)}\otimes \rho _{1}^{(3)})\right] \\&\quad \cdot \mathrm {tr} \left[ \frac{A^{2,2}_{0}+ A^{2,2}_{1} }{2} \rho _{3}^{(2)}\right] \cdot \mathrm {tr} \left[ \left( \frac{A^{3,1}_{0}+ A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}+ A^{3,2}_{1} }{2}\right) \rho _{23}^{(3)}\right] \\&= \mathrm {tr} \left[ \frac{\sigma _{z}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}} \otimes \sigma _{z}\otimes \sigma _{z}\otimes \sigma _{z}\otimes \sigma _{z}\right) \right. \\&\quad \left. \cdot \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle + \sqrt{3}|1\rangle }{2} \right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{z}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}}\otimes \frac{\sigma _{z}+ \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] =-\frac{1}{64}, \end{aligned}$$

$$\begin{aligned} K_{\{1\}}&= \mathrm {tr} \left[ \frac{A^{1,1}_{0}- A^{1,1}_{1} }{2}\rho _{1}^{(1)}\right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{2,1}_{0}- A^{2,1}_{1} }{2}\otimes B_{y_{\{1\}}}\otimes C_{z_{\{1\}}}\right) (\rho _{12}^{(2)}\otimes \rho _{23}^{(1)}\otimes \rho _{1}^{(3)})\right] \\&\quad \cdot \mathrm {tr} \left[ \frac{A^{2,2}_{0}+ A^{2,2}_{1} }{2} \rho _{3}^{(2)}\right] \cdot \mathrm {tr} \left[ \left( \frac{A^{3,1}_{0}- A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}+ A^{3,2}_{1} }{2}\right) \rho _{23}^{(3)}\right] \\&= \mathrm {tr} \left[ \frac{\sigma _{x}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}} \otimes \sigma _{x}\otimes \sigma _{z}\otimes \sigma _{z}\otimes \sigma _{x}\right) \right. \\&\quad \left. \cdot \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle + \sqrt{3}|1\rangle }{2} \right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{z}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{z}+ \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] = -\frac{3}{64}, \end{aligned}$$

$$\begin{aligned} K_{\{2\}}&= \mathrm {tr} \left[ \frac{A^{1,1}_{0}+ A^{1,1}_{1} }{2}\rho _{1}^{(1)}\right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{2,1}_{0}+ A^{2,1}_{1} }{2}\otimes B_{y_{\{2\}}}\otimes C_{z_{\{2\}}}\right) (\rho _{12}^{(2)}\otimes \rho _{23}^{(1)}\otimes \rho _{1}^{(3)})\right] \\&\quad \cdot \mathrm {tr} \left[ \frac{A^{2,2}_{0}- A^{2,2}_{1} }{2} \rho _{3}^{(2)}\right] \cdot \mathrm {tr} \left[ \left( \frac{A^{3,1}_{0}+ A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}- A^{3,2}_{1} }{2}\right) \rho _{23}^{(3)}\right] \\&= \mathrm {tr} \left[ \frac{\sigma _{z}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}} \otimes \sigma _{z}\otimes \sigma _{x}\otimes \sigma _{x}\otimes \sigma _{z}\right) \right. \\&\quad \left. \cdot \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle + \sqrt{3}|1\rangle }{2} \right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{x}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}}\otimes \frac{\sigma _{z}- \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] =\frac{\sqrt{3}}{64} \end{aligned}$$

and

$$\begin{aligned} K_{\{1,2\}}&= \mathrm {tr} \left[ \frac{A^{1,1}_{0}- A^{1,1}_{1} }{2}\rho _{1}^{(1)}\right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{2,1}_{0}- A^{2,1}_{1} }{2}\otimes B_{y_{\{1,2\}}}\otimes C_{z_{\{1,2\}}}\right) (\rho _{12}^{(2)}\otimes \rho _{23}^{(1)}\otimes \rho _{1}^{(3)})\right] \\&\quad \cdot \mathrm {tr} \left[ \frac{A^{2,2}_{0}- A^{2,2}_{1} }{2} \rho _{3}^{(2)}\right] \cdot \mathrm {tr} \left[ \left( \frac{A^{3,1}_{0}- A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}- A^{3,2}_{1} }{2}\right) \rho _{23}^{(3)}\right] \\&= \mathrm {tr} \left[ \frac{\sigma _{x}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}} \otimes \sigma _{x}\otimes \sigma _{x}\otimes \sigma _{x}\otimes \sigma _{x}\right) \right. \\&\quad \left. \cdot \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle + \sqrt{3}|1\rangle }{2} \right) \right] \\&\quad \cdot \mathrm {tr} \left[ \frac{\sigma _{x}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{z}- \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&= -\frac{3\sqrt{3}}{64}. \end{aligned}$$

Thus

$$\begin{aligned} \sum \limits _{X\in \mathbb {P}(\mathbb {N}_{L})}|K_{X}|^{\frac{1}{3}}&= |K_{\emptyset }|^{\frac{1}{3}}+ |K_{\{1\}}|^{\frac{1}{3}}+ |K_{\{2\}}|^{\frac{1}{3}}+ |K_{\{1,2\}}|^{\frac{1}{3}}\\&= \left| -\frac{1}{64}\right| ^{\frac{1}{3}}+ |-\frac{3}{64}|^{\frac{1}{3}}+ \left| \frac{\sqrt{3}}{64}\right| ^{\frac{1}{3}}+ \left| -\frac{3\sqrt{3}}{64}\right| ^{\frac{1}{3}}\\&= \frac{1}{4}(1+ \root 3 \of {3}+ \root 6 \of {3}+ \sqrt{3})> 2^{\frac{1}{3}}, \end{aligned}$$

violating the 3-local inequality (5).

Group 6

This group contains 1 case as listed in Table 6.

Table 6 Only case of specific bipartition for $\rho _1$, $\rho _2$ and $\rho _3$

Take $|\varphi _{(23|1)}^1\rangle = |\varphi _{(23|1)}^2\rangle = |\varphi _{(23|1)}^3\rangle =\frac{|00\rangle + |11\rangle }{\sqrt{2}}\otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}$. Write $\rho _1=\rho ^{(1)}_{1} \otimes \rho ^{(1)}_{23}$, $\rho _2=\rho ^{(2)}_{1} \otimes \rho ^{(2)}_{23}$ and $\rho _3=\rho ^{(3)}_{1} \otimes \rho ^{(3)}_{23}$. Assume the parties $A^{1,1}$, $A^{2,1}$, $A^{3,1}$ perform the measurements $A^{1,1}_{0}= A^{2,1}_{0}= A^{3,1}_{0}=\frac{\sigma _{z}+ \sigma _{x}}{\sqrt{2}}$ and $A^{1,1}_{1} = A^{2,1}_{1}= A^{3,1}_{1}=\frac{\sigma _{z}- \sigma _{x}}{\sqrt{2}}$, while the parties $A^{2,2}$, $A^{3,2}$ perform the measurements $A^{2,2}_{0}=A^{3,2}_{0}=\sigma _{z}$ and $A^{2,2}_{1}=A^{3,2}_{1}=\sigma _{x}$. Assume the measurement choices of parties B and C are $\{\sigma _{z} \otimes \sigma _{z}$, $\sigma _{z} \otimes \sigma _{x}$, $\sigma _{x} \otimes \sigma _{z}$, $\sigma _{x} \otimes \sigma _{x}\}$, respectively.

In this case, Eq. (A3) reduces to

$$\begin{aligned} K_{X}&= \mathrm {tr} \left[ \frac{A^{1,1}_{0}+ (-1)^{\delta ^1_{X_{1}}}A^{1,1}_{1} }{2}\rho _{1}^{(1)}\right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{2,1}_{0}+ (-1)^{\delta ^1_{X_{2}}}A^{2,1}_{1} }{2}\otimes \frac{A^{2,2}_{0}+ (-1)^{\delta ^2_{X_{2}}}A^{2,2}_{1} }{2}\right) \rho _{23}^{(2)}\right] \\&\quad \cdot \mathrm {tr} \left[ (B_{y_{X}}\otimes C_{z_{X}}) (\rho _{1}^{(2)}\otimes \rho _{23}^{(1)}\otimes \rho _{1}^{(3)})\right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{3,1}_{0}+ (-1)^{\delta ^1_{X_{3}}}A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}+ (-1)^{\delta ^2_{X_{3}}}A^{3,2}_{1} }{2}\right) \rho _{23}^{(3)}\right] . \end{aligned}$$

By taking $B_{y_{\emptyset }}=\sigma _{z}\otimes \sigma _{z}$ and $C_{z_{\emptyset }}=\sigma _{z}\otimes \sigma _{z}$, $B_{y_{\{1\}}}=\sigma _{x}\otimes \sigma _{z}$ and $C_{z_{\{1\}}}=\sigma _{z}\otimes \sigma _{x}$, $B_{y_{\{2\}}}=\sigma _{z}\otimes \sigma _{x}$ and $C_{z_{\{2\}}}=\sigma _{x}\otimes \sigma _{z}$ $B_{y_{\{1,2\}}}=\sigma _{x}\otimes \sigma _{x}$ and $C_{z_{\{1,2\}}}=\sigma _{x}\otimes \sigma _{x}$, respectively, we obtain

$$\begin{aligned} K_{\emptyset }&= \mathrm {tr} \left[ \frac{A^{1,1}_{0}+ A^{1,1}_{1} }{2}\rho _{1}^{(1)}\right] \cdot \mathrm {tr} \left[ \left( \frac{A^{2,1}_{0}+ A^{2,1}_{1} }{2}\otimes \frac{A^{2,2}_{0}+ A^{2,2}_{1} }{2}\right) \rho _{23}^{(2)}\right] \\&\quad \cdot \mathrm {tr} [(B_{y_{\emptyset }}\otimes C_{z_{\emptyset }}) (\rho _{1}^{(2)}\otimes \rho _{23}^{(1)}\otimes \rho _{1}^{(3)})]\\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{3,1}_{0}+ A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}+ A^{3,2}_{1} }{2}\right) \rho _{23}^{(3)}\right] \\&= \mathrm {tr} \left[ \frac{\sigma _{z}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ (\sigma _{z}\otimes \sigma _{z}\otimes \sigma _{z}\otimes \sigma _{z}) \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle + \sqrt{3}|1\rangle }{2} \right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}}\otimes \frac{\sigma _{z}+ \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}}\otimes \frac{\sigma _{z}+ \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] =-\frac{1}{64\sqrt{2}}, \end{aligned}$$

$$\begin{aligned} K_{\{1\}}&= \mathrm {tr} \left[ \frac{A^{1,1}_{0}- A^{1,1}_{1} }{2}\rho _{1}^{(1)}\right] \cdot \mathrm {tr} \left[ \left( \frac{A^{2,1}_{0}- A^{2,1}_{1} }{2}\otimes \frac{A^{2,2}_{0}+ A^{2,2}_{1} }{2}\right) \rho _{23}^{(2)}\right] \\&\quad \cdot \mathrm {tr} [(B_{y_{\{1\}}}\otimes C_{z_{\{1\}}}) (\rho _{1}^{(2)}\otimes \rho _{23}^{(1)}\otimes \rho _{1}^{(3)})]\\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{3,1}_{0}- A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}+ A^{3,2}_{1} }{2}\right) \rho _{23}^{(3)}\right] \\&= \mathrm {tr} \left[ \frac{\sigma _{x}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ (\sigma _{x}\otimes \sigma _{z}\otimes \sigma _{z}\otimes \sigma _{x}) \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle + \sqrt{3}|1\rangle }{2} \right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{z}+ \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{z}+ \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] =\frac{3\sqrt{3}}{64\sqrt{2}}, \end{aligned}$$

$$\begin{aligned} K_{\{2\}}&= \mathrm {tr} \left[ \frac{A^{1,1}_{0}+ A^{1,1}_{1} }{2}\rho _{1}^{(1)}\right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{2,1}_{0}+ A^{2,1}_{1} }{2}\otimes \frac{A^{2,2}_{0}- A^{2,2}_{1} }{2}\right) \rho _{23}^{(2)}\right] \\&\quad \cdot \mathrm {tr} [(B_{y_{\{2\}}}\otimes C_{z_{\{2\}}}) (\rho _{1}^{(2)}\otimes \rho _{23}^{(1)}\otimes \rho _{1}^{(3)})]\\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{3,1}_{0}+ A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}- A^{3,2}_{1} }{2}\right) \rho _{23}^{(3)}\right] \\&= \mathrm {tr} \left[ \frac{\sigma _{z}}{\sqrt{2}} \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ (\sigma _{x}\otimes \sigma _{z}\otimes \sigma _{z}\otimes \sigma _{x}) \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle + \sqrt{3}|1\rangle }{2} \right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}}\otimes \frac{\sigma _{z}- \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}}\otimes \frac{\sigma _{z}- \sigma _{x}}{2}) (\frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] =-\frac{3}{64\sqrt{2}} \end{aligned}$$

and

$$\begin{aligned} K_{\{1,2\}}&= \mathrm {tr} \left[ \frac{A^{1,1}_{0}- A^{1,1}_{1} }{2}\rho _{1}^{(1)}\right] \cdot \mathrm {tr} \left[ \left( \frac{A^{2,1}_{0}- A^{2,1}_{1} }{2}\otimes \frac{A^{2,2}_{0}- A^{2,2}_{1} }{2}\right) \rho _{23}^{(2)}\right] \\&\quad \cdot \mathrm {tr} [(B_{y_{\{1,2\}}}\otimes C_{z_{\{1,2\}}}) (\rho _{1}^{(2)}\otimes \rho _{23}^{(1)}\otimes \rho _{1}^{(3)})]\\&\quad \cdot \mathrm {tr} \left[ \left( \frac{A^{3,1}_{0}- A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}- A^{3,2}_{1} }{2}\right) \rho _{23}^{(3)}\right] \\&= \mathrm {tr} \left[ \frac{\sigma _{x}}{\sqrt{2}} (\frac{|0\rangle + \sqrt{3}|1\rangle }{2})\right] \\&\quad \cdot \mathrm {tr} \left[ (\sigma _{x}\otimes \sigma _{x}\otimes \sigma _{x}\otimes \sigma _{x}) \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2} \otimes \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|0\rangle + \sqrt{3}|1\rangle }{2}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{z}- \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{z}- \sigma _{x}}{2}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}}\right) \right] = \frac{3\sqrt{3}}{64\sqrt{2}}. \end{aligned}$$

Therefore

$$\begin{aligned} \sum \limits _{X\in \mathbb {P}(\mathbb {N}_{L})}|K_{X}|^{\frac{1}{3}}&= |K_{\emptyset }|^{\frac{1}{3}}+ |K_{\{1\}}|^{\frac{1}{3}}+ |K_{\{2\}}|^{\frac{1}{3}}+ |K_{\{1,2\}}|^{\frac{1}{3}}\\&= \left| -\frac{1}{64\sqrt{2}}\right| ^{\frac{1}{3}}+ \left| \frac{3\sqrt{3}}{64\sqrt{2}}\right| ^{\frac{1}{3}}+ \left| -\frac{3}{64\sqrt{2}}\right| ^{\frac{1}{3}}+ \left| \frac{3\sqrt{3}}{64\sqrt{2}}\right| ^{\frac{1}{3}}\\&= \frac{1}{2\root 6 \of {2}} (1+2 \sqrt{3} + \root 3 \of {3})> 2^{\frac{1}{3}}, \end{aligned}$$

violating the 3-local inequality (5).

In one word, for any one of 27 forms of the overall quantum state, there always exist specific examples to violate the 3-local inequality (5) by choosing suitable measurements.

Appendix D

1.1 1. Quantum violation of three GHZ states in network of Fig. 3

Let all the sources $S_{i}$ $(i=1,2,3)$ emit three-qubit GHZ state $\rho _i=|\mathrm {GHZ}\rangle \langle \mathrm {GHZ}|$. Assume the parties $A^{1,1}$, $A^{2,1}$, $A^{2,2}$, $A^{3,1}$, $A^{3,2}$ perform the measurements $A^{1,1}_{0}= A^{2,1}_{0}=A^{2,2}_{0}= A^{3,1}_{0}=A^{3,2}_{0}=\frac{\sigma _{x}+ \sigma _{y}}{\sqrt{2}}$, $A^{1,1}_{1} =A^{2,1}_{1}=A^{2,2}_{1}=A^{3,1}_{1}= A^{3,2}_{1}=\frac{\sigma _{x}- \sigma _{y}}{\sqrt{2}}$. The measurement choices of parties B and C are $\{\sigma _{x} \otimes \sigma _{x}$, $\sigma _{x} \otimes \sigma _{y}$, $\sigma _{y} \otimes \sigma _{x}$, $\sigma _{y} \otimes \sigma _{y}\}$, respectively.

By Eq. (A3), taking $B_{y_{\emptyset }}=\sigma _{x}\otimes \sigma _{x}$ and $C_{z_{\emptyset }}=\sigma _{x}\otimes \sigma _{x}$, one gets

$$\begin{aligned} K_{\emptyset }&= \mathrm {tr} \left[ \left( \frac{ A^{1,1}_{0}+ A^{1,1}_{1}}{2}\otimes B_{y_{\emptyset }} \otimes C_{z_{\emptyset }} \otimes \frac{ A^{2,1}_{0}+ A^{2,1}_{1}}{2}\otimes \frac{ A^{2,2}_{0}+ A^{2,2}_{1}}{2}\right. \right. \\&\quad \left. \left. \otimes \frac{ A^{3,1}_{0}+ A^{3,1}_{1}}{2}\otimes \frac{ A^{3,2}_{0}+ A^{3,2}_{1}}{2}\right) \cdot (\rho _{1}\otimes \rho _{2}\otimes \rho _{3})\right] \\&= \mathrm {tr}\left[ \left( \frac{ \sigma _{x}}{\sqrt{2}} \otimes \sigma _{x} \otimes \sigma _{x}\otimes \sigma _{x} \otimes \sigma _{x}\right. \right. \\&\quad \left. \left. \otimes \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{x}}{\sqrt{2}} \right) (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] \\&=\frac{1}{4\sqrt{2}}; \end{aligned}$$

taking $B_{y_{\{1\}}}=\sigma _{y}\otimes \sigma _{y}$ and $C_{z_{\{1\}}}=\sigma _{y}\otimes \sigma _{x}$ (or $\sigma _{x}\otimes \sigma _{y}$) gives

$$\begin{aligned} K_{\{1\}}&= \mathrm {tr} \left[ \left( \frac{ A^{1,1}_{0}- A^{1,1}_{1}}{2} \otimes B_{y_{\{1\}}} \otimes C_{z_{\{1\}}} \otimes \frac{ A^{2,1}_{0}- A^{2,1}_{1}}{2} \otimes \frac{ A^{2,2}_{0}+ A^{2,2}_{1}}{2} \right. \right. \\&\left. \left. \quad \otimes \frac{ A^{3,1}_{0}- A^{3,1}_{1}}{2} \otimes \frac{ A^{3,2}_{0}+ A^{3,2}_{1}}{2} \right) \cdot (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] \\&= \mathrm {tr} \left[ \left( \frac{ \sigma _{y}}{\sqrt{2}} \otimes \sigma _{y} \otimes \sigma _{y}\otimes \sigma _{y} \otimes \sigma _{x}\otimes \frac{\sigma _{y}}{\sqrt{2}}\otimes \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{y}}{\sqrt{2}}\right. \right. \\&\quad \left. \left. \otimes \frac{\sigma _{x}}{\sqrt{2}} \right) (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] = -\frac{1}{4\sqrt{2}}; \end{aligned}$$

taking $B_{y_{\{2\}}}=\sigma _{y}\otimes \sigma _{y}$ and $C_{z_{\{2\}}}=\sigma _{y}\otimes \sigma _{y}$ yields

$$\begin{aligned} K_{\{2\}}&= \mathrm {tr} \left[ \left( \frac{ A^{1,1}_{0}+ A^{1,1}_{1}}{2} \otimes B_{y_{\{2\}}} \otimes C_{z_{\{2\}}} \otimes \frac{ A^{2,1}_{0}+ A^{2,1}_{1}}{2} \otimes \frac{ A^{2,2}_{0}- A^{2,2}_{1}}{2}\right. \right. \\&\quad \left. \left. \otimes \frac{ A^{3,1}_{0}+ A^{3,1}_{1}}{2} \otimes \frac{ A^{3,2}_{0}- A^{3,2}_{1}}{2}\right) \cdot (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] \\&= \mathrm {tr}\left[ \left( \frac{ \sigma _{x}}{\sqrt{2}} \otimes \sigma _{y} \otimes \sigma _{y}\otimes \sigma _{y} \otimes \sigma _{y}\otimes \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{y}}{\sqrt{2}}\otimes \frac{\sigma _{x}}{\sqrt{2}}\right. \right. \\&\quad \left. \left. \otimes \frac{\sigma _{y}}{\sqrt{2}} \right) (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] = -\frac{1}{4\sqrt{2}}; \end{aligned}$$

and taking $B_{y_{\{1, 2\}}}=\sigma _{x}\otimes \sigma _{y}$ (or $\sigma _{y}\otimes \sigma _{x}$) and $C_{z_{\{1, 2\}}}=\sigma _{x}\otimes \sigma _{x}$ gives

$$\begin{aligned} K_{\{1,2\}}&= \mathrm {tr} \left[ \left( \frac{ A^{1,1}_{0}- A^{1,1}_{1}}{2}\otimes B_{y_{\{1,2\}}} \otimes C_{z_{\{1,2\}}} \otimes \frac{ A^{2,1}_{0}- A^{2,1}_{1}}{2} \otimes \frac{ A^{2,2}_{0}- A^{2,2}_{1}}{2} \right. \right. \\&\quad \left. \left. \otimes \frac{ A^{3,1}_{0}- A^{3,1}_{1}}{2} \otimes \frac{ A^{3,2}_{0}- A^{3,2}_{1}}{2}\right) \cdot (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] \\&= \mathrm {tr}\left[ \left( \frac{ \sigma _{y}}{\sqrt{2}} \otimes \sigma _{y} \otimes \sigma _{x}\otimes \sigma _{x} \otimes \sigma _{x}\otimes \frac{\sigma _{y}}{\sqrt{2}}\otimes \frac{\sigma _{y}}{\sqrt{2}}\otimes \frac{\sigma _{y}}{\sqrt{2}}\right. \right. \\&\quad \left. \left. \otimes \frac{\sigma _{y}}{\sqrt{2}} \right) (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] = -\frac{1}{4\sqrt{2}}. \end{aligned}$$

Therefore,

$$\begin{aligned} \sum \limits _{X\in \mathbb {P}(\mathbb {N}_{L})}|K_{X}|^{\frac{1}{3}}&= |K_{\emptyset }|^{\frac{1}{3}}+ |K_{\{1\}}|^{\frac{1}{3}}+ |K_{\{2\}}|^{\frac{1}{3}}+ |K_{\{1,2\}}|^{\frac{1}{3}}\\&= 4\times \left| \frac{1}{4\sqrt{2}}\right| ^{\frac{1}{3}} = 2\root 6 \of {2} >2^{\frac{1}{3}}, \end{aligned}$$

violating the 3-local inequality (5).

1.2 2. Quantum violation of three W states in network of Fig. 3

Let all the sources $S_{i}$ $(i=1,2,3)$ produce W state $\rho _i=|\varphi _{W}\rangle \langle \varphi _{W}|$ with $|\varphi _{W}\rangle =\frac{1}{\sqrt{3}} (|100\rangle + |010\rangle + |001\rangle )$. In this case, we assume that the parties $A^{1,1}$, $A^{2,1}$, $A^{2,2}$, $A^{3,1}$, $A^{3,2}$ perform the measurements $A^{1,1}_{0}= A^{2,1}_{0}=A^{2,2}_{0}= A^{3,1}_{0}=A^{3,2}_{0}= \frac{\sigma _{z}+ \sigma _{x}}{\sqrt{2}}$, $A^{1,1}_{1} =A^{2,1}_{1}=A^{2,2}_{1}=A^{3,1}_{1}= A^{3,2}_{1}=\frac{\sigma _{z}- \sigma _{x}}{\sqrt{2}}$. For parties B and C, we choose $B_{y_{\emptyset }}=\sigma _{z}\otimes \sigma _{z}$, $C_{z_{\emptyset }}=\sigma _{z}\otimes \sigma _{z}$, $B_{y_{\{1\}}}=\sigma _{x}\otimes \sigma _{x}$, $C_{z_{\{1\}}}=\sigma _{z}\otimes \sigma _{x}$, $B_{y_{\{2\}}}=\sigma _{z}\otimes \sigma _{x}$, $C_{z_{\{2\}}}=\sigma _{x}\otimes \sigma _{z}$, and $B_{y_{\{1, 2\}}}=\sigma _{x}\otimes \sigma _{z}$, $C_{z_{\{1, 2\}}}=\sigma _{z}\otimes \sigma _{z}$. It follows from Eq. (A3) that

$$\begin{aligned} K_{\emptyset }&= \mathrm {tr} \left[ \left( \frac{ A^{1,1}_{0}+ A^{1,1}_{1}}{2}\otimes B_{y_{\emptyset }} \otimes C_{z_{\emptyset }} \otimes \frac{ A^{2,1}_{0}+ A^{2,1}_{1}}{2}\otimes \frac{ A^{2,2}_{0}+ A^{2,2}_{1}}{2}\right. \right. \\&\quad \left. \left. \otimes \frac{ A^{3,1}_{0}+ A^{3,1}_{1}}{2}\otimes \frac{ A^{3,2}_{0}+ A^{3,2}_{1}}{2}\right) \cdot (\rho _{1}\otimes \rho _{2}\otimes \rho _{3})\right] \\&= \mathrm {tr}\left[ \left( \frac{ \sigma _{z}}{\sqrt{2}} \otimes \sigma _{z} \otimes \sigma _{z}\otimes \sigma _{z} \otimes \sigma _{z}\otimes \frac{\sigma _{z}}{\sqrt{2}}\otimes \frac{\sigma _{z}}{\sqrt{2}}\otimes \frac{\sigma _{z}}{\sqrt{2}}\right. \right. \\&\quad \left. \left. \otimes \frac{\sigma _{z}}{\sqrt{2}} \right) (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] = -\frac{1}{4\sqrt{2}}, \end{aligned}$$

$$\begin{aligned} K_{\{1\}}&= \mathrm {tr}\left[ \left( \frac{ A^{1,1}_{0}- A^{1,1}_{1}}{2} \otimes B_{y_{\{1\}}} \otimes C_{z_{\{1\}}} \otimes \frac{ A^{2,1}_{0}- A^{2,1}_{1}}{2} \otimes \frac{ A^{2,2}_{0}+ A^{2,2}_{1}}{2} \right. \right. \\&\quad \left. \left. \otimes \frac{ A^{3,1}_{0}- A^{3,1}_{1}}{2} \otimes \frac{ A^{3,2}_{0}+ A^{3,2}_{1}}{2} \right) \cdot (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] \\&= \mathrm {tr}\left[ \left( \frac{ \sigma _{x}}{\sqrt{2}} \otimes \sigma _{x} \otimes \sigma _{x}\otimes \sigma _{z} \otimes \sigma _{x}\otimes \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{z}}{\sqrt{2}}\otimes \frac{\sigma _{x}}{\sqrt{2}}\right. \right. \\&\quad \left. \left. \otimes \frac{\sigma _{z}}{\sqrt{2}} \right) (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] = \frac{\sqrt{2}}{27}, \end{aligned}$$

$$\begin{aligned} K_{\{2\}}&= \mathrm {tr} \left[ \left( \frac{ A^{1,1}_{0}+ A^{1,1}_{1}}{2} \otimes B_{y_{\{2\}}} \otimes C_{z_{\{2\}}} \otimes \frac{ A^{2,1}_{0}+ A^{2,1}_{1}}{2} \otimes \frac{ A^{2,2}_{0}- A^{2,2}_{1}}{2} \right. \right. \\&\quad \left. \left. \otimes \frac{ A^{3,1}_{0}+ A^{3,1}_{1}}{2} \otimes \frac{ A^{3,2}_{0}- A^{3,2}_{1}}{2}\right) \cdot (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] \\&= \mathrm {tr}\left[ \left( \frac{ \sigma _{z}}{\sqrt{2}} \otimes \sigma _{z} \otimes \sigma _{x}\otimes \sigma _{x} \otimes \sigma _{z}\otimes \frac{\sigma _{z}}{\sqrt{2}}\otimes \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{z}}{\sqrt{2}}\right. \right. \\&\quad \left. \left. \otimes \frac{\sigma _{x}}{\sqrt{2}} \right) (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] = -\frac{1}{9\sqrt{2}} \end{aligned}$$

and

$$\begin{aligned} K_{\{1,2\}}&= \mathrm {tr} \left[ \left( \frac{ A^{1,1}_{0}- A^{1,1}_{1}}{2}\otimes B_{y_{\{1,2\}}} \otimes C_{z_{\{1,2\}}} \otimes \frac{ A^{2,1}_{0}- A^{2,1}_{1}}{2} \otimes \frac{ A^{2,2}_{0}- A^{2,2}_{1}}{2} \right. \right. \\&\quad \left. \left. \otimes \frac{ A^{3,1}_{0}- A^{3,1}_{1}}{2} \otimes \frac{ A^{3,2}_{0}- A^{3,2}_{1}}{2}\right) \cdot (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] \\&= \mathrm {tr}\left[ \left( \frac{ \sigma _{x}}{\sqrt{2}} \otimes \sigma _{x} \otimes \sigma _{z}\otimes \sigma _{z} \otimes \sigma _{z}\otimes \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{x}}{\sqrt{2}}\right. \right. \\&\quad \left. \left. \otimes \frac{\sigma _{x}}{\sqrt{2}} \right) (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] = \frac{\sqrt{2}}{27}. \end{aligned}$$

Thus

$$\begin{aligned} \sum \limits _{X\in \mathbb {P}(\mathbb {N}_{L})}|K_{X}|^{\frac{1}{3}}&= |K_{\emptyset }|^{\frac{1}{3}}+ |K_{\{1\}}|^{\frac{1}{3}}+ |K_{\{2\}}|^{\frac{1}{3}}+ |K_{\{1,2\}}|^{\frac{1}{3}}\\&= \left| -\frac{1}{4\sqrt{2}}\right| ^{\frac{1}{3}}+ \left| \frac{\sqrt{2}}{27}\right| ^{\frac{1}{3}}+ \left| -\frac{1}{9\sqrt{2}}\right| ^{\frac{1}{3}}+ \left| \frac{\sqrt{2}}{27}\right| ^{\frac{1}{3}}\\&= \frac{1}{\root 6 \of {32}} \left( 1+\frac{4}{3} + \root 3 \of {\frac{4}{9}}\right) > 2^{\frac{1}{3}}, \end{aligned}$$

violating the 3-local inequality (5).

Appendix E: Quantum violation of one biseparable entangled pure state and two genuine entangled pure states in network of Fig. 3

Let the source $S_1$ produce biseparable entangled pure state $\rho _1= |\varphi _{(12|3)}^1\rangle \langle \varphi _{(12|3)}^1|$ with $|\varphi _{(12|3)}^1\rangle = \frac{|00\rangle + |11\rangle }{\sqrt{2}}\otimes \frac{|0\rangle +\sqrt{3}|1\rangle }{2}$, and the sources $S_2$, $S_3$ produce W states $\rho _2= \rho _3= |\varphi _{W}\rangle \langle \varphi _{W}|$. Write $\rho _1=\rho _{12}^{(1)}\otimes \rho _{3}^{(1)}$. Assume the parties $A^{1,1}$, $A^{2,1}$, $A^{2,2}$, $A^{3,1}$, $A^{3,2}$ perform the measurements $A^{1,1}_{0}= A^{2,1}_{0}= A^{2,2}_{0}=A^{3,1}_{0}=A^{3,2}_{0}=\frac{\sigma _{z}+ \sigma _{x}}{\sqrt{2}}$ and $A^{1,1}_{1} = A^{2,1}_{1}=A^{2,2}_{1}= A^{3,1}_{1}=A^{3,2}_{1}= \frac{\sigma _{z}- \sigma _{x}}{\sqrt{2}}$. The measurement choices of parties B and C are from $\{\sigma _{z} \otimes \sigma _{z}$, $\sigma _{z} \otimes \sigma _{x}$, $\sigma _{x} \otimes \sigma _{z}$, $\sigma _{x} \otimes \sigma _{x}\}$, respectively.

In this case, Eq. (A3) reduces to

$$\begin{aligned} K_{X}&= \mathrm {tr} \left[ \left( \frac{A^{1,1}_{0}+ (-1)^{\delta ^1_{X_{1}}}A^{1,1}_{1} }{2}\otimes B_{y_{X}}\otimes \frac{A^{2,1}_{0}+ (-1)^{\delta ^1_{X_{2}}}A^{2,1}_{1} }{2}\right. \right. \\&\quad \left. \left. \otimes \frac{A^{2,2}_{0}+ (-1)^{\delta ^2_{X_{2}}}A^{2,2}_{1} }{2}\right) (\rho _{12}^{(1)}\otimes \rho _2)\right] \\&\quad \cdot \mathrm {tr} \left[ \left( C_{z_{X}}\otimes \frac{A^{3,1}_{0}+ (-1)^{\delta ^1_{X_{3}}}A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}+ (-1)^{\delta ^2_{X_{3}}}A^{3,2}_{1} }{2}\right) (\rho _{3}^{(1)}\otimes \rho _{3})\right] . \end{aligned}$$

Choose $B_{y_{\emptyset }}=\sigma _{z}\otimes \sigma _{z}$, $C_{z_{\emptyset }}=\sigma _{z}\otimes \sigma _{z}$; then

$$\begin{aligned} K_{\emptyset }&= \mathrm {tr} \left[ \left( \frac{A^{1,1}_{0}+ A^{1,1}_{1} }{2}\otimes B_{y_{\emptyset }}\otimes \frac{A^{2,1}_{0}+ A^{2,1}_{1} }{2}\otimes \frac{A^{2,2}_{0}+ A^{2,2}_{1} }{2}\right) (\rho _{12}^{(1)}\otimes \rho _2)\right] \\&\quad \cdot \mathrm {tr} \left[ \left( C_{z_{\emptyset }}\otimes \frac{A^{3,1}_{0}+ A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}+ A^{3,2}_{1} }{2}\right) (\rho _{3}^{(1)}\otimes \rho _{3})\right] \\&= \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}} \otimes \sigma _{z}\otimes \sigma _{z}\otimes \frac{\sigma _{z}}{\sqrt{2}} \otimes \frac{\sigma _{z}}{\sqrt{2}}\right) \!\! \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|100\rangle + |010\rangle + |001\rangle }{\sqrt{3}} \right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \sigma _{z}\otimes \sigma _{z}\otimes \frac{\sigma _{z}}{\sqrt{2}}\otimes \frac{\sigma _{z}}{\sqrt{2}}\right) \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2} \otimes \frac{|100\rangle + |010\rangle + |001\rangle }{\sqrt{3}}\right) \right] \\&= -\frac{1}{8\sqrt{2}}. \end{aligned}$$

Choose $B_{y_{\{1\}}}=\sigma _{x}\otimes \sigma _{x}$, $C_{z_{\{1\}}}=\sigma _{x}\otimes \sigma _{x}$; then

$$\begin{aligned} K_{\{1\}}&= \mathrm {tr} \left[ \left( \frac{A^{1,1}_{0}- A^{1,1}_{1} }{2}\otimes B_{y_{\{1\}}}\otimes \frac{A^{2,1}_{0}- A^{2,1}_{1} }{2}\otimes \frac{A^{2,2}_{0}+ A^{2,2}_{1} }{2}\right) (\rho _{12}^{(1)}\otimes \rho _2)\right] \\&\quad \cdot \mathrm {tr} \left[ \left( C_{z_{\{1\}}}\otimes \frac{A^{3,1}_{0}- A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}+ A^{3,2}_{1} }{2}\right) (\rho _{3}^{(1)}\otimes \rho _{3})\right] \\&= \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}} \otimes \sigma _{x}\otimes \sigma _{x}\otimes \frac{\sigma _{x}}{\sqrt{2}} \otimes \frac{\sigma _{z}}{\sqrt{2}}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|100\rangle + |010\rangle + |001\rangle }{\sqrt{3}} \right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \sigma _{x}\otimes \sigma _{x}\otimes \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{z}}{\sqrt{2}}\right) \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2} \otimes \frac{|100\rangle + |010\rangle + |001\rangle }{\sqrt{3}}\right) \right] \\&=\frac{1}{6\sqrt{6}}. \end{aligned}$$

Choose $B_{y_{\{2\}}}=\sigma _{z}\otimes \sigma _{x}$, $C_{z_{\{2\}}}=\sigma _{z}\otimes \sigma _{x}$; then

$$\begin{aligned} K_{\{2\}}= & {} \mathrm {tr} \left[ \left( \frac{A^{1,1}_{0}+ A^{1,1}_{1} }{2}\otimes B_{y_{\{2\}}}\otimes \frac{A^{2,1}_{0}+ A^{2,1}_{1} }{2}\otimes \frac{A^{2,2}_{0}- A^{2,2}_{1} }{2}\right) (\rho _{12}^{(1)}\otimes \rho _2)\right] \\&\cdot \mathrm {tr} \left[ \left( C_{z_{\{2\}}}\otimes \frac{A^{3,1}_{0}+ A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}- A^{3,2}_{1} }{2}\right) (\rho _{3}^{(1)}\otimes \rho _{3})\right] \\= & {} \mathrm {tr} \left[ \left( \frac{\sigma _{z}}{\sqrt{2}} \otimes \sigma _{z}\otimes \sigma _{x}\otimes \frac{\sigma _{z}}{\sqrt{2}} \otimes \frac{\sigma _{x}}{\sqrt{2}}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|100\rangle + |010\rangle + |001\rangle }{\sqrt{3}} \right) \right] \\&\cdot \mathrm {tr} \left[ \left( \sigma _{z}\otimes \sigma _{x}\otimes \frac{\sigma _{z}}{\sqrt{2}}\otimes \frac{\sigma _{x}}{\sqrt{2}}\right) \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2} \otimes \frac{|100\rangle + |010\rangle + |001\rangle }{\sqrt{3}}\right) \right] \\= & {} -\frac{1}{18\sqrt{2}}. \end{aligned}$$

Choose $B_{y_{\{1,2\}}}=\sigma _{x}\otimes \sigma _{z}$, $C_{z_{\{1,2\}}}=\sigma _{x}\otimes \sigma _{z}$; then

$$\begin{aligned} K_{\{1,2\}}&= \mathrm {tr} \left[ \left( \frac{A^{1,1}_{0}- A^{1,1}_{1} }{2}\otimes B_{y_{\{1,2\}}}\otimes \frac{A^{2,1}_{0}- A^{2,1}_{1} }{2}\otimes \frac{A^{2,2}_{0}- A^{2,2}_{1} }{2}\right) (\rho _{12}^{(1)}\otimes \rho _2)\right] \\&\quad \cdot \mathrm {tr} \left[ \left( C_{z_{\{1,2\}}}\otimes \frac{A^{3,1}_{0}- A^{3,1}_{1} }{2} \otimes \frac{A^{3,2}_{0}- A^{3,2}_{1} }{2}\right) (\rho _{3}^{(1)}\otimes \rho _{3})\right] \\&= \mathrm {tr} \left[ \left( \frac{\sigma _{x}}{\sqrt{2}} \otimes \sigma _{x}\otimes \sigma _{z}\otimes \frac{\sigma _{x}}{\sqrt{2}} \otimes \frac{\sigma _{x}}{\sqrt{2}}\right) \left( \frac{|00\rangle + |11\rangle }{\sqrt{2}} \otimes \frac{|100\rangle + |010\rangle + |001\rangle }{\sqrt{3}} \right) \right] \\&\quad \cdot \mathrm {tr} \left[ \left( \sigma _{x}\otimes \sigma _{z}\otimes \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{x}}{\sqrt{2}}\right) \left( \frac{|0\rangle + \sqrt{3}|1\rangle }{2} \otimes \frac{|100\rangle + |010\rangle + |001\rangle }{\sqrt{3}}\right) \right] \\&=\frac{1}{6\sqrt{6}}. \end{aligned}$$

Thus

$$\begin{aligned} \sum \limits _{X\in \mathbb {P}(\mathbb {N}_{L})}|K_{X}|^{\frac{1}{3}}&= |K_{\emptyset }|^{\frac{1}{3}}+ |K_{\{1\}}|^{\frac{1}{3}}+ |K_{\{2\}}|^{\frac{1}{3}}+ |K_{\{1,2\}}|^{\frac{1}{3}}\\&= \left| -\frac{1}{8\sqrt{2}}\right| ^{\frac{1}{3}}+ \left| \frac{1}{6\sqrt{6}}\right| ^{\frac{1}{3}}+ \left| -\frac{1}{18\sqrt{2}}\right| ^{\frac{1}{3}}+ \left| \frac{1}{6\sqrt{6}}\right| ^{\frac{1}{3}}\\&= \frac{1}{2\root 6 \of {2}}+ \sqrt{\frac{2}{3}}+ \frac{1}{\sqrt{2}}\cdot \frac{1}{\root 3 \of {9}}> 2^{\frac{1}{3}}, \end{aligned}$$

violating the 3-local inequality (5). This implies the non-3-local correlation nature.

Appendix F: Quantum violation of three GHZ symmetric states distributed in network of Fig. 3

Suppose all the sources $S_i$ $(i=1,2,3)$ produce GHZ symmetric state

$$\begin{aligned} \rho _i&= \left( \frac{2p_2}{\sqrt{3}}+ p_1\right) |\mathrm {GHZ}_{+}\rangle \langle \mathrm {GHZ}_{+}| + \left( \frac{2p_2}{\sqrt{3}}- p_1\right) |\mathrm {GHZ}_{-}\rangle \langle \mathrm {GHZ}_{-}|\\&\quad +\left( 1-\frac{4p_2}{\sqrt{3}}\right) \frac{\mathbb {I}}{8}. \end{aligned}$$

Let the parties $A^{1,1}$, $A^{2,1}$, $A^{2,2}$, $A^{3,1}$, $A^{3,2}$ perform the measurements $A^{1,1}_{0}= A^{2,1}_{0}=A^{2,2}_{0}= A^{3,1}_{0}=A^{3,2}_{0}=\frac{\sigma _{x}+ \sigma _{y}}{\sqrt{2}}$, $A^{1,1}_{1} =A^{2,1}_{1}=A^{2,2}_{1}=A^{3,1}_{1}= A^{3,2}_{1}=\frac{\sigma _{x}- \sigma _{y}}{\sqrt{2}}$, and parties B, C perform measurements from $\{\sigma _{x} \otimes \sigma _{x}$, $\sigma _{x} \otimes \sigma _{y}$, $\sigma _{y} \otimes \sigma _{x}$, $\sigma _{y} \otimes \sigma _{y}\}$, respectively.

According to Eq. (A3), we choose $B_{y_{\emptyset }}=\sigma _{x}\otimes \sigma _{x}$, $C_{z_{\emptyset }}=\sigma _{x}\otimes \sigma _{x}$, which yields

$$\begin{aligned} K_{\emptyset }&= \mathrm {tr} \left[ \left( \frac{ A^{1,1}_{0}+ A^{1,1}_{1}}{2}\otimes B_{y_{\emptyset }} \otimes C_{z_{\emptyset }} \otimes \frac{ A^{2,1}_{0}+ A^{2,1}_{1}}{2}\otimes \frac{ A^{2,2}_{0}+ A^{2,2}_{1}}{2}\right. \right. \\&\quad \left. \left. \otimes \frac{ A^{3,1}_{0}+ A^{3,1}_{1}}{2}\otimes \frac{ A^{3,2}_{0}+ A^{3,2}_{1}}{2}\right) \cdot (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] \\&= \mathrm {tr}\left[ \left( \frac{ \sigma _{x}}{\sqrt{2}} \otimes \sigma _{x} \otimes \sigma _{x}\otimes \sigma _{x} \otimes \sigma _{x}\otimes \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{x}}{\sqrt{2}}\right. \right. \\&\quad \left. \left. \otimes \frac{\sigma _{x}}{\sqrt{2}} \right) (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] = \sqrt{2} (p_1)^3. \end{aligned}$$

Similarly, choosing $B_{y_{\{1\}}}=\sigma _{y}\otimes \sigma _{y}$ and $C_{z_{\{1\}}}=\sigma _{y}\otimes \sigma _{x}$ (or $\sigma _{x}\otimes \sigma _{y}$) gives

$$\begin{aligned} K_{\{1\}}&= \mathrm {tr} \left[ \left( \frac{ A^{1,1}_{0}- A^{1,1}_{1}}{2} \otimes B_{y_{\{1\}}} \otimes C_{z_{\{1\}}} \otimes \frac{ A^{2,1}_{0}- A^{2,1}_{1}}{2} \otimes \frac{ A^{2,2}_{0}+ A^{2,2}_{1}}{2}\right. \right. \\&\quad \left. \left. \otimes \frac{ A^{3,1}_{0}- A^{3,1}_{1}}{2} \otimes \frac{ A^{3,2}_{0}+ A^{3,2}_{1}}{2} \right) \cdot (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] \\&= \mathrm {tr} \left[ \left( \frac{ \sigma _{y}}{\sqrt{2}} \otimes \sigma _{y} \otimes \sigma _{y}\otimes \sigma _{y} \otimes \sigma _{x}\otimes \frac{\sigma _{y}}{\sqrt{2}}\otimes \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{y}}{\sqrt{2}}\right. \right. \\&\quad \left. \left. \otimes \frac{\sigma _{x}}{\sqrt{2}} \right) (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] = -\sqrt{2} (p_1)^3; \end{aligned}$$

choosing $B_{y_{\{2\}}}=\sigma _{y}\otimes \sigma _{y}$ and $C_{z_{\{2\}}}=\sigma _{y}\otimes \sigma _{y}$ gives

$$\begin{aligned} K_{\{2\}}&= \mathrm {tr} \left[ \left( \frac{ A^{1,1}_{0}+ A^{1,1}_{1}}{2} \otimes B_{y_{\{2\}}} \otimes C_{z_{\{2\}}} \otimes \frac{ A^{2,1}_{0}+ A^{2,1}_{1}}{2} \otimes \frac{ A^{2,2}_{0}- A^{2,2}_{1}}{2} \right. \right. \\&\quad \left. \left. \otimes \frac{ A^{3,1}_{0}+ A^{3,1}_{1}}{2} \otimes \frac{ A^{3,2}_{0}- A^{3,2}_{1}}{2}\right) \cdot (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] \\&= \mathrm {tr}\left[ \left( \frac{ \sigma _{x}}{\sqrt{2}} \otimes \sigma _{y} \otimes \sigma _{y}\otimes \sigma _{y} \otimes \sigma _{y}\otimes \frac{\sigma _{x}}{\sqrt{2}}\otimes \frac{\sigma _{y}}{\sqrt{2}}\otimes \frac{\sigma _{x}}{\sqrt{2}}\right. \right. \\&\quad \left. \left. \otimes \frac{\sigma _{y}}{\sqrt{2}} \right) (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] = -\sqrt{2} (p_1)^3; \end{aligned}$$

choosing $B_{y_{\{1, 2\}}}=\sigma _{x}\otimes \sigma _{y}$ (or $\sigma _{y}\otimes \sigma _{x}$) and $C_{z_{\{1, 2\}}}=\sigma _{x}\otimes \sigma _{x}$ leads to

$$\begin{aligned} K_{\{1,2\}}&= \mathrm {tr} \left[ \left( \frac{ A^{1,1}_{0}- A^{1,1}_{1}}{2}\otimes B_{y_{\{1,2\}}} \otimes C_{z_{\{1,2\}}} \otimes \frac{ A^{2,1}_{0}- A^{2,1}_{1}}{2} \otimes \frac{ A^{2,2}_{0}- A^{2,2}_{1}}{2} \right. \right. \\&\quad \left. \left. \otimes \frac{ A^{3,1}_{0}- A^{3,1}_{1}}{2} \otimes \frac{ A^{3,2}_{0}- A^{3,2}_{1}}{2}\right) \cdot (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] \\&= \mathrm {tr}\left[ \left( \frac{ \sigma _{y}}{\sqrt{2}} \otimes \sigma _{y} \otimes \sigma _{x}\otimes \sigma _{x} \otimes \sigma _{x}\otimes \frac{\sigma _{y}}{\sqrt{2}}\otimes \frac{\sigma _{y}}{\sqrt{2}}\otimes \frac{\sigma _{y}}{\sqrt{2}}\right. \right. \\&\quad \left. \left. \otimes \frac{\sigma _{y}}{\sqrt{2}} \right) (\rho _{1}\otimes \rho _{2}\otimes \rho _{3}) \right] = -\sqrt{2} (p_1)^3. \end{aligned}$$

Hence

$$\begin{aligned} \sum \limits _{X\in \mathbb {P}(\mathbb {N}_{L})}|K_{X}|^{\frac{1}{3}} = |K_{\emptyset }|^{\frac{1}{3}}+ |K_{\{1\}}|^{\frac{1}{3}}+ |K_{\{2\}}|^{\frac{1}{3}}+ |K_{\{1,2\}}|^{\frac{1}{3}}=4 \root 6 \of {2} |p_1|. \end{aligned}$$

Now it is clear that, if $|p_1| >\frac{1}{2\root 6 \of {32}}$, then $\sum _{X\in \mathbb {P}(\mathbb {N}_{L})}|K_{X}|^{\frac{1}{3}}> 2^{\frac{1}{3}}$, violating the 3-local inequality (5) and implying non-3-local correlations.