Skip to main content
Springer Nature Link
Log in

Quantum multi-secret sharing via trap codes and discrete quantum walks

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

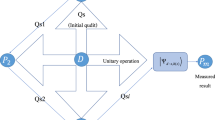
In this paper, we propose a fully quantum multi-secret sharing scheme. In contrast with regular secret sharing schemes, multi-secret sharing schemes share a set of unknown secrets, and during the reconstruction phase, all the secrets are reconstructed. The main technique is to suitably modify a quantum trap code to construct a scheme where increasing number of secret states are recovered as more and more participants combine their shares. It is desirable that the dimensions of the share states are within implementable limits. In view of this and due to the significantly large dimension of the share states produced by our first construction, we introduce a discrete-time quantum walk-based technique to reduce the dimension of the shares making the schemes more suitable for practical purposes. Our methods are unconditional and do not depend on any computational hardness assumptions like lattice-based problems. Our scheme is simple, secure against adversarial attacks and can be easily modified into several variants of multi-secret sharing schemes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.

Abbreviations

\({\mathbb {N}}\), \({\mathbb {Z}}\), \({\mathbb {C}}\) :

Natural numbers, integers, complex numbers

\({\mathcal {P}}\), \(p_{i}\) :

Set of participants, i-th participant

\(\Gamma \), \(\Gamma _{YES}\), \(\Gamma _{NO}\) :

Access structure, qualified sets, forbidden sets

(n, k):

k-out-of-n threshold access structure

\(t_{i}\) :

i-th threshold

S, \({\mathcal {S}}\) :

Domain of secrets

(SHARE, RECON):

Secret sharing scheme

\(\Pi _{i}^{(s)}\) :

Distribution on share of i-th participant

\(I, X, \sigma _{x}, Y, Z, \sigma _{z}\) :

Pauli matrices

\({\mathbb {P}}_{n}\) :

Set of n-qubit Pauli matrices

[n]:

\(\{1,2, \ldots , n\}\)

\(\sigma \), \(\sigma _{n_{i}}\), \(\sigma _{k_{i}}\) :

Permutation map (not to be confused with the Pauli operators)

\(\left| \phi \right\rangle \) :

Qubit/quantum state/secret

\(Sh_{Th}(n,k), Rec_{Th}(n,k)\) :

Fully quantum threshold secret sharing scheme

\(Share_{k,n}, Rec_{k,n}\) :

Semi-quantum threshold secret sharing scheme

U, R, C, S, F, G :

Unitary operators

\(E_{ij}\) :

Elementary matrix

\({[}C_{1}, \ldots , C_{d}{]}\) :

Block diagonal matrix

SSS:

Secret sharing scheme

MSSS:

Multi-secret sharing scheme

QSSS:

Quantum secret sharing scheme

QMSSS:

Quantum multi-secret sharing scheme

QECC:

Quantum error-correcting code

References

  1. Shamir, A.: How to share a secret. Commun. ACM 22(11), 612–613 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  2. Blakley, G.R.: Safeguarding cryptographic keys. In: International Workshop On Managing Requirements Knowledge, pp. 313–313. IEEE Computer Society (1979)

  3. Blundo, C., Santis, A.D., Crescenzo, G.D., Gaggia, A.G., Vaccaro, U.: Multi-secret sharing schemes. In: Annual International Cryptology Conference, pp. 150–163. Springer (1994)

  4. Dijk, M.V., Jackson, W.-A., Martin, K.M.: A general decomposition construction for incomplete secret sharing schemes. Des. Codes Cryptogr. 15(3), 301–321 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  5. Tartary, C., Pieprzyk, J., Wang, H.: Verifiable multi-secret sharing schemes for multiple threshold access structures. In: International Conference on Information Security and Cryptology, pp. 167–181. Springer (2007)

  6. Dehkordi, M.H., Mashhadi, S.: New efficient and practical verifiable multi-secret sharing schemes. Inf. Sci. 178(9), 2262–2274 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  7. Beimel, A., Ben-Efraim, A., Padró, C., Tyomkin, I.: Multi-linear secret-sharing schemes. In: Theory of Cryptography Conference, pp. 394–418. Springer (2014)

  8. Jackson, W.-A., Martin, K.M., O’Keefe, C.M.: Multisecret threshold schemes. In: Annual International Cryptology Conference, pp. 126–135. Springer (1993)

  9. Masucci, B.: Sharing multiple secrets: models, schemes and analysis. Des. Codes Cryptogr. 39(1), 89–111 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  10. Waseda, A., Soshi, M.: Consideration for multi-threshold multi-secret sharing schemes. In: 2012 International Symposium on Information Theory and Its Applications, pp. 265–269. IEEE (2012)

  11. Herranz, J., Ruiz, A., Sáez, G.: New results and applications for multi-secret sharing schemes. Des. Codes Cryptogr. 73(3), 841–864 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  12. Amroudi, A.N., Zaghain, A., Sajadieh, M.: A verifiable (k, n, m)-threshold multi-secret sharing scheme based on ntru cryptosystem. Wirel. Pers. Commun. 96(1), 1393–1405 (2017)

    Article  Google Scholar 

  13. Pilaram, H., Eghlidos, T.: A lattice-based changeable threshold multi-secret sharing scheme and its application to threshold cryptography. Sci. Iran. 24(3), 1448–1457 (2017)

    Google Scholar 

  14. Hou, Y.-C., Quan, Z.-Y.: Progressive visual cryptography with unexpanded shares. IEEE Trans. Circuits Syst. Video Technol. 21(11), 1760–1764 (2011)

    Article  Google Scholar 

  15. Prasetyo, H., Hsia, C.-H., Wicaksono Hari Prayuda, A.: Progressive secret sharing with adaptive priority and perfect reconstruction. J. Imaging 7(4), 70 (2021)

    Article  Google Scholar 

  16. Anbarasi, L.J., Mala, G.A.: Survey and analysis of visual secret sharing techniques. Comput. Softw., p. 1507 (2014)

  17. Gottesman, D.: Theory of quantum secret sharing. Phys. Rev. A 61(4), 042311 (2000)

    Article  ADS  MathSciNet  Google Scholar 

  18. Mosca, M., Tapp, A., de Wolf, R.: Private quantum channels and the cost of randomizing quantum information (2000). arXiv:quant-ph/0003101

  19. Lu, H., Zhang, Z., Chen, L.-K., Li, Z.-D., Liu, C., Li, L., Liu, N.-L., Ma, X., Chen, Y.-A., Pan, J.-W.: Secret sharing of a quantum state. Phys. Rev. Lett. 117(3), 030501 (2016)

    Article  ADS  Google Scholar 

  20. Qin, H., Zhu, X., Dai, Y.: (t, n) threshold quantum secret sharing using the phase shift operation. Quantum Inf. Process. 14(8), 2997–3004 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  21. Qin, H., Dai, Y.: Verifiable (t, n) threshold quantum secret sharing using d-dimensional bell state. Inf. Process. Lett. 116(5), 351–355 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  22. Song, X.-L., Liu, Y.-B., Deng, H.-Y., Xiao, Y.-G.: (t, n) threshold d-level quantum secret sharing. Sci. Rep. 7(1), 1–9 (2017)

    ADS  Google Scholar 

  23. Qin, H., Tso, R., Dai, Y.: Multi-dimensional quantum state sharing based on quantum Fourier transform. Quantum Inf. Process. 17(3), 1–12 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  24. Mashhadi, S.: General secret sharing based on quantum Fourier transform. Quantum Inf. Process. 18(4), 1–15 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  25. Zhou, Q., Lv, H.: Multi-secret sharing model based on Hermite interpolation polynomial and quantum graph state. Int. J. Theor. Phys. 59(8), 2271–2293 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  26. Chen, H., Wu, H.-L., Chang, C.-C., Chen, L.-S.: Light repository blockchain system with multisecret sharing for industrial big data. Secur. Commun. Netw. 2019(1), 7 (2019) https://doi.org/10.1155/2019/9060756

  27. Mesnager, S., Sınak, A., Yayla, O.: Threshold-based post-quantum secure verifiable multi-secret sharing for distributed storage blockchain. Mathematics 8(12), 2218 (2020)

    Article  Google Scholar 

  28. Zhang, Z.-j, Li, Y., Man, Z.-x: Multiparty quantum secret sharing. Phys. Rev. A 71(4), 044301 (2005)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  29. Zhang, Z.-j, Man, Z.-x: Multiparty quantum secret sharing of classical messages based on entanglement swapping. Phys. Rev. A 72(2), 022303 (2005)

    Article  ADS  MathSciNet  Google Scholar 

  30. Da-Zu, H., Zhi-Gang, C., Ying, G.: Multiparty quantum secret sharing using quantum Fourier transform. Commun. Theor. Phys. 51(2), 221 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  31. Smania, M., Elhassan, A.M., Tavakoli, A., Bourennane, M.: Experimental quantum multiparty communication protocols. Npj Quantum Inf. 2(1), 1–4 (2016)

    Article  Google Scholar 

  32. Karimipour, V., Asoudeh, M.: Quantum secret sharing and random hopping: using single states instead of entanglement. Phys. Rev. A 92(3), 030301 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  33. Lu, C., Miao, F., Hou, J., Ning, Y.: Quantum walk based quantum secret sharing in a verifiable framework. In: 2021 2nd International Conference on Big Data & Artificial Intelligence & Software Engineering (ICBASE), pp. 271–276. IEEE (2021)

  34. Guo, G.-P., Guo, G.-C.: Quantum secret sharing without entanglement. Phys. Lett. A 310(4), 247–251 (2003)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  35. Yan, F.-L., Gao, T.: Quantum secret sharing between multiparty and multiparty without entanglement. Phys. Rev. A 72(1), 012304 (2005)

    Article  ADS  Google Scholar 

  36. Chandrashekar, C.M., Srikanth, R., Laflamme, R.: Optimizing the discrete time quantum walk using a su (2) coin. Phys. Rev. A 77(3), 032326 (2008)

    Article  ADS  Google Scholar 

  37. Childs, A.M.: On the relationship between continuous-and discrete-time quantum walk. Commun. Math. Phys. 294(2), 581–603 (2010)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  38. Szegedy, M.: Quantum speed-up of markov chain based algorithms. In: 45th Annual IEEE Symposium on Foundations of Computer Science, pp. 32–41. IEEE (2004)

  39. Ambainis, A.: Quantum walk algorithm for element distinctness. SIAM J. Comput. 37(1), 210–239 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  40. Lovett, N.B., Cooper, S., Everitt, M., Trevers, M., Kendon, V.: Universal quantum computation using the discrete-time quantum walk. Phys. Rev. A 81(4), 042330 (2010)

    Article  ADS  MathSciNet  Google Scholar 

  41. Godsil, C., Zhan, H.: Discrete-time quantum walks and graph structures. J. Comb. Theory Ser. A 167, 181–212 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  42. Watrous, J.: Quantum simulations of classical random walks and undirected graph connectivity. J. Comput. Syst. Sci. 62(2), 376–391 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  43. Aharonov, D., Ambainis, A., Kempe, J., Vazirani, U.: Quantum walks on graphs. In: Proceedings of the Thirty-Third Annual ACM Symposium on Theory of Computing, pp. 50–59 (2001)

  44. Kendon, V.: Quantum walks on general graphs. Int. J. Quantum Inf. 4(05), 791–805 (2006)

    Article  MATH  Google Scholar 

  45. Yan, X., Lu, Y., Liu, L.: A general progressive secret image sharing construction method. Signal Process. Image Commun. 71, 66–75 (2019)

    Article  Google Scholar 

  46. Song, X., Wang, S., Sang, J., Yan, X., Niu, X.: Flexible quantum image secret sharing based on measurement and strip. In: 2014 Tenth International Conference on Intelligent Information Hiding and Multimedia Signal Processing, pp. 215–218. IEEE (2014)

  47. Wang, H.-Q., Song, X.-H., Chen, L.-L., Xie, W.: A secret sharing scheme for quantum gray and color images based on encryption. Int. J. Theor. Phys. 58(5), 1626–1650 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  48. Portugal, R.: Quantum Walks and Search Algorithms, vol. 19. Springer, Berlin (2013)

    Book  MATH  Google Scholar 

  49. Samadder Chaudhury, S.: A quantum evolving secret sharing scheme. Int. J. Theor. Phys. 59(12), 3936–3950 (2020)

    Article  MATH  Google Scholar 

  50. Chaudhury, S.S.: On quantum evolving secret sharing schemes-further studies and improvements. Quantum Inf. Comput. 21(5 &6), 0385–0407 (2022)

    MathSciNet  Google Scholar 

  51. Broadbent, A., Gutoski, G., Stebila, D.: Quantum one-time programs. In: Annual Cryptology Conference, pp. 344–360. Springer (2013)

  52. Broadbent, A., Wainewright, E.: Efficient simulation for quantum message authentication. In: International Conference on Information Theoretic Security, pp. 72–91. Springer (2016)

  53. Broadbent, A., Jeffery, S.: Quantum homomorphic encryption for circuits of low t-gate complexity. In: Annual Cryptology Conference, pp. 609–629. Springer (2015)

  54. Cheng, K., Ishai, Y., Li, X.: Near-optimal secret sharing and error correcting codes in ac0. In: Kalai, Y., Reyzin, L. (eds.) Theory of Cryptography—15th International Conference, TCC 2017, Baltimore, MD, USA, November 12–15, 2017, Proceedings, Part II (2017)

  55. Komargodski, I., Naor, M., Yogev, E.: How to share a secret, infinitely. IEEE Trans. Inf. Theory 64(6), 4179–4190 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  56. Zhan, H.: Quantum walks on embeddings. J. Algebr. Comb. 53(4), 1187–1213 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  57. Bai, C.-M., Li, Z.-H., Si, M.-M., Li, Y.-M.: Quantum secret sharing for a general quantum access structure. Eur. Phys. J. D 71(10), 1–8 (2017)

    Article  ADS  Google Scholar 

  58. Wang, M.-M., Chen, X.-B., Yang, Y.-X.: Quantum secret sharing for general access structures based on multiparticle entanglements. Quantum Inf. Process. 13(2), 429–443 (2014)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  59. Nascimento, A.C., Mueller-Quade, J., Imai, H.: Improving quantum secret-sharing schemes. Phys. Rev. A 64(4), 042311 (2001)

    Article  ADS  Google Scholar 

  60. Dajka, J., Łuczka, J., Hänggi, P.: Distance between quantum states in the presence of initial qubit-environment correlations: a comparative study. Phys. Rev. A 84(3), 032120 (2011)

    Article  ADS  Google Scholar 

  61. Singh, S.K., Srikanth, R.: Generalized quantum secret sharing. Phys. Rev. A 71(1), 012328 (2005)

    Article  ADS  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors thank the anonymous reviewers whose careful and insightful comments helped in correcting various errors and largely improved the quality of the manuscript. The first author thanks TCG Centres for Research and Education in Science and Technology for a post-doctoral fellowship which financially supported this work. Second author was financially supported by MITACS Accelerate fellowship, Canada vide Ref. No. IT25625, FR66861. The authors also thank Bimal Kr. Roy and Goutam Mukherjee for stimulating discussions.

Author information

Authors and Affiliations

  1. Translational Research in Mathematics, TCG Centres for Research and Education in Science and Technology, Salt Lake Sector V, Kolkata, West Bengal, 700091, India

    Shion Samadder Chaudhury

  2. Department of Computer Science, University of Calgary, University Dr NW, Calgary, AB, T2N 1N4, Canada

    Sabyasachi Dutta

Authors
  1. Shion Samadder Chaudhury
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Sabyasachi Dutta
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Shion Samadder Chaudhury.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Samadder Chaudhury, S., Dutta, S. Quantum multi-secret sharing via trap codes and discrete quantum walks. Quantum Inf Process 21, 380 (2022). https://doi.org/10.1007/s11128-022-03732-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-022-03732-1

Keywords

Mathematics Subject Classification