Finite sampling bandwidth effect on practical security of discretely modulated continuous-variable quantum key distribution

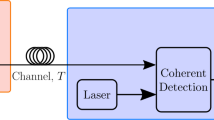
Abstract

Finite sampling bandwidth of analog-to-digital converter (ADC) has an effect on performance of continuous-variable quantum key distribution (CVQKD). The matter results in a considerable decrease in performance and leaves the practical security of the system, brought on by a safe loophole exploited by eavesdropper to launch the potential attacks. The linear relationship between secret key rate and repetition frequency is thus restrained from this challenge. To seek and deal with such a loophole in CVQKD with discrete modulation, we suggest a dual sampling detection approach that involves two ADCs in data processing. Security analysis shows that the performance of the discretely modulated (DM) CVQKD system can be improved in terms of the secret key rate and maximal transmission distance. The practical security of DM CVQKD is therefore demonstrated, thereby providing a theoretical proof for applying the DM CVQKD system to a realistic environment.

Appendix

1.1 A Discrete Fourier transformation of the signal

Sampling is a process where continuous signal is converted to a discrete sequence of values. By periodically sampling continuous signal, the discrete signal is thus derived. Practical sampling frequency and sampling duration of on-off keying (OOK) are finite. Given the finite sampling frequency, it is likely that information loss introduced by sample interval may leave a loophole, exploited by the eavesdropper.

Generally, with regard to finite-pulse-width sampling system, sampling duration tends to be too short to have effects on the performance of on-off keying. The sampling duration is even shorter than sampling period, so the former approaches zero. Under such circumstance, the sampling process is therefore regarded as amplitude modulation. The theoretical sampler functions as amplitude modulation with carrier wave $\delta _T(t)$, which represents unit impulse sequence. After amplitude modulation, the carrier wave then carries the information of continuous signal. Each unit impulse duration approaches zero, the intensity of which mainly depends on the instantaneous amplitude. Therefore, the amplitude modulation is depicted as follows:

$$\begin{aligned} \begin{aligned} e^*(t)=e(t)\delta _T(t) \end{aligned}. \end{aligned}$$

(10)

The unit impulse sequence is written as follows:

$$\begin{aligned} \begin{aligned} \delta _T(t)=\sum _{n=0}^\infty \delta (t-nT) \end{aligned}, \end{aligned}$$

(11)

where $\delta (t-nT)$ represents unit impulse when $t=nT$. e(t) can be rewritten as

$$\begin{aligned} \begin{aligned} e^*(t)=e(t)\sum _{n=0}^\infty \delta (t-nT) \end{aligned}. \end{aligned}$$

(12)

The corresponding instantaneous modulated amplitude is shown as follows,

$$\begin{aligned} \begin{aligned} e^*(t)=e(nt)\sum _{n=0}^\infty \delta (t-nT) \end{aligned}. \end{aligned}$$

(13)

Under the condition of the causal system in practice, we suppose that the impulse sequence is casual signal, namely $e(t)=0, \forall t<0$. By Laplace transforming sampling signal $e^*(t)$, the modulated amplitude is rewritten as follows:

$$\begin{aligned} \begin{aligned} E^*(s)={\mathscr {L}}[e^*(t)]={\mathscr {L}}[\sum _{n=0}^\infty e(nt)\delta (t-nT)] \end{aligned}. \end{aligned}$$

(14)

According to the displacement theorem of Laplace transformation, the impulse can be rewritten as

$$\begin{aligned} \begin{aligned} {\mathscr {L}}[\delta (t-nT)]=e^{-nTs}\int _0^\infty \delta (t)e^{-st}dt=e^{-nTs} \end{aligned}. \end{aligned}$$

(15)

As for modulated sampling signal, we can then derive it after Laplace transformation,

$$\begin{aligned} \begin{aligned} E^*(s)=\sum _{n=0}^\infty e(nT)e^{-nTs} \end{aligned}. \end{aligned}$$

(16)

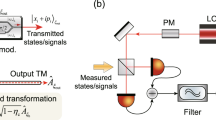
As a result, each instantaneous sampling signal can be derived above. As long as the sampling frequency is satisfactory, there is a slim chance that lots of information is lost before signal rebuilding. From Fig. 1b, we can draw a conclusion that it is though to sample the peak value. There exists the deviation to the peak value when measuring the voltage, which, obviously, has effects on the secret key rate and transmission distance. The reason why there is an obvious drop of the secret key rate and transmission distance is that the extra electrical noise is introduced by practical ADC. In the time domain, we can visually explore the deviation between measured value and peak value due to finite sampling frequency.

To demonstrate the deviation in the frequency domain, we then analyze the frequency spectrum of the sampling signal. As is mentioned above, it is because of information loss resulting from finite sampling frequency that the frequency spectrum of continuous signal varies a lot after sampling.

In order to better illustrate the principle in the frequency domain, we take the frequency spectrum of arbitrary sampling signal as an example. Unit impulse sequence is a periodical function, the expansion of which can be rewritten as follows:

$$\begin{aligned} \begin{aligned} \delta _T(t)=\sum _{n=-\infty }^\infty c_ne^{jn\omega _st} \end{aligned}, \end{aligned}$$

(17)

where $\omega _s=2\pi /t$ represents sampling angular frequency, and $c_n$ represents Laplace coefficient, namely

$$\begin{aligned} \begin{aligned} c_n=\frac{1}{T}\int _{-\frac{T}{2}}^{\frac{T}{2}}\delta _T(t)e^{-jn\omega _st}dt \end{aligned}. \end{aligned}$$

(18)

According to the definition of the unit impulse, only when $t=0$ is the value equal to unit value. We thus further simplify the calculation of $c_n$0 as

$$\begin{aligned} \begin{aligned} c_n=\frac{1}{T}\int _{0_-}^{0_+}\delta (t)dt=\frac{1}{T} \end{aligned}. \end{aligned}$$

(19)

Then Eq. 18 can also be rewritten as follows:

$$\begin{aligned} \begin{aligned} \delta _T(t)=\frac{1}{T}\sum _{n=-\infty }^{\infty }e^{jn\omega _st} \end{aligned}. \end{aligned}$$

(20)

The following equation is therefore derived,

$$\begin{aligned} \begin{aligned} e^*=\frac{1}{T}\sum _{n=-\infty }^{\infty }e(t)e^{jn\omega _st} \end{aligned}. \end{aligned}$$

(21)

By Laplace transforming the aforementioned equation, we can easily obtain

$$\begin{aligned} \begin{aligned} E^*(s)=\frac{1}{T}\sum _{n=-\infty }^{\infty }E(s+jn\omega _s) \end{aligned}. \end{aligned}$$

(22)

Suppose that there are no poles in the half-right plane (HRP) for the purpose of a stable system, we therefore assume that $s=j\omega$. Finally, we Laplace transform the sampling signal $e^*(t)$, namely

$$\begin{aligned} \begin{aligned} E^*(j\omega )=\frac{1}{T}\sum _{n=-\infty }^{\infty }E(j\omega +jn\omega _s) \end{aligned}. \end{aligned}$$

(23)

Generally, we can see that the frequency spectrum of continuous signal is continuous. $\omega _h$ represents the maximal angular frequency, while $\omega _h$ represents infinite period of repetition frequency introduced by sampling signal. When $n=0$, the frequency spectrum shapes like that of continuous signal. With the increase in angular frequency, it may lead to frequency aliasing. Generally, given the finite sampling frequency of ADC, it sometimes may not meet our needs, especially when $\omega _s<2\omega _h$ the frequency spectrum of original continuous signal and sampling signal overlaps. Unfortunately, due to signal distortion, the continuous signal can by no means be rebuilt any more even with the help of filters. Therefore, we finally draw a conclusion that in case of signal distortion, $\omega _s<2\omega _h$ is a necessary condition when choosing ADC.

As for the aforementioned practical homodyne or heterodyne detector, the field of quadrature value is proportional to the output signal of each impulse. As seen in Fig. 1b, we may conclude that sufficient sampling points should be guaranteed and integrated for each impulse. To overcome the obstacle which brings more challenges to data processing, it is assumed that impulse duration is much shorter than sampling. Therefore, the shape of homodyne or heterodyne detection depends on deriving response function. Based on the above assumption, the quadrature is linearly proportional to the maximal value of homodyne or heterodyne detection.

To assume the each output impulse shapes like Gaussian function, described as

$$\begin{aligned} \begin{aligned} r(t)=U_pe^{-\frac{{(t-\mu )}^2}{2\sigma ^2}}=U_pe^{-\frac{{(t-t_0/2)}^2}{t_0^2/32}}, \end{aligned} \end{aligned}$$

(24)

where $U_p$ represents the maximal value of each Gaussian impulse, $\mu$ is the mean, and $\sigma ^2$ represents variance.

As for the ideal CVQKD scheme, the maximal value of each Gaussian impulse is therefore measured, after which the measured quadrature is linearly proportional to the maximal value. Unfortunately, finite sampling bandwidth leads to the deviation to the peak value, as seen in Fig. 1b. $t_s$ represents sampling duration, and the sampling bandwidth is described as $f_{samp}=1/t_s\ Hz$. The maximal discrepancy between the maximal value and the measured value is described as

$$\begin{aligned} \begin{aligned} \Delta \le U_p-U_m=U_p\left[ 1-exp(\frac{t_s^2}{8\sigma ^2})\right] \end{aligned}, \end{aligned}$$

(25)

and the ratio between $U_m$ and $U_p$ is defined by

$$\begin{aligned} \begin{aligned} k=\frac{U_m}{U_p}\in \left[ exp(-\frac{8f_{\mathrm{{rep}}}^2}{f_{samp}^2}),1\right] \end{aligned}, \end{aligned}$$

(26)

which shows that the defined ratio is related to sampling bandwidth and repetition frequency.

1.2 B Derivation of covariance matrixes

In this section, after discrete modulation, the mixture state $\rho _4$ can be expressed as

$$\begin{aligned} \begin{aligned} \rho _4&=Tr(|\Psi _4\rangle \langle \Psi _4|)\\&=\sum _{k=0}^{3}|\Phi _4\rangle \langle \Phi _4|. \end{aligned} \end{aligned}$$

(27)

We have known that the mode A and the mode B denote the measurements of coherent states detected by Alice and Bob, respectively. Then, we derive the following covariance matrix $\Gamma _{AB}^4$ of the bipartite state $|\Psi \rangle _4$,

$$\begin{aligned} \begin{aligned} \Gamma _{AB}= \begin{pmatrix} V_A{\mathbb {I}} &{} Z_4\sigma _z \\ Z_4\sigma _z &{} V_B{\mathbb {I}} \end{pmatrix} , \end{aligned} \end{aligned}$$

(28)

where ${\mathbb {I}}$ and $\sigma _z$ represent the diagonal matrix diag(1,1) and diag(1,-1), respectively.

To acquire the analytical expression of security key rate, we propose the covariance matrix $\Gamma _{AB_1}$ of the inequivalent EB-based version of our scheme after passing through the public quantum channel. Firstly, the covariance matrix of the EPR-state that Alice prepared can be given by the following expression,

$$\begin{aligned} \begin{aligned} \Gamma _{AB1}= \begin{pmatrix} V_A{\mathbb {I}} &{} C_1\sigma _z \\ C_1\sigma _z &{} V_{B_1}{\mathbb {I}} \end{pmatrix} , \end{aligned} \end{aligned}$$

(29)

where $C_1=\sqrt{T}Z_4$, $V_{B_1}=T(V_B+\chi _{line})$ with $\chi _{line}=1/T-1+\xi$. The covariance matrix can then be derived as follows:

$$\begin{aligned} \begin{aligned} \Gamma _{AB2}= \begin{pmatrix} V_A{\mathbb {I}} &{} C_2\sigma _z \\ C_2\sigma _z &{} V_{B_2}{\mathbb {I}} \end{pmatrix} \end{aligned} \end{aligned}$$

(30)

with

$$\begin{aligned} \begin{aligned} V_{B_2}=\eta T(V_B&+\chi _{line}/\eta +\chi _{det}/T), \\ C_2&=\sqrt{C_1}, \end{aligned} \end{aligned}$$

(31)

where $\chi _{det}=(1-\eta +\xi _{el})\eta$ for homodyne detection and $\chi _{det}=(2-\eta +2\xi _{el})\eta$ for heterodyne detection. In addition, to obtain the covariance matrix of the eight-state DM CVQKD protocol, we shall only replace $Z_4$ with $Z_8$.

1.3 C Calculation of the secret key rate

In this section, the secret key rate analysis is mainly carried out under Gaussian collective attacks, simply because they are proved to be optimal in asymptotic cases. Additionally, the asymptotic security analysis has already been proved, while the finite-size and composable security analysis has not been proved. We now calculate the secret key rate of Four-state and Eight-state DM CVQKD.

As mentioned in Sect. 3, four-state and eight-state protocols are suggested in the scheme. Alice sends one of the coherent states to Bob, the possibility of which is 1/4 or 1/8. Alice discretely modulates the coherent states into four or eight states.

To obtain the lower bound of the secret key rate, the covariance matrix in the asymptotic framework thus should be derived. The secret key rate in the case of asymptotic security for heterodyne detection reads

$$\begin{aligned} \begin{aligned} K={\beta }I_{AB}-\chi _{BE} \end{aligned}, \end{aligned}$$

(32)

while the secret key rate for homodyne detection reads as follows:

$$\begin{aligned} \begin{aligned} K=\frac{1}{2}[{\beta }I_{AB}-\chi _{BE}] \end{aligned}, \end{aligned}$$

(33)

where $\beta$ is the reconciliation efficiency, $I_{AB}$ refers to the mutual information shared by both Alice and Bob, and $\chi _{BE}$ represents the Holevo bound between Bob and Eve for reverse reconciliation. The mutual information can be derived by the following expression

$$\begin{aligned} \begin{aligned} I_{AB}=\frac{1}{2}log_2\frac{V_A}{V_{A|B_3}} \end{aligned}, \end{aligned}$$

(34)

where $V_A=(V+1)/2$, is the amplitude quadrature variance for Alice, which is the first element of matrix $\gamma _A$ describing mode A, and $V_{A|B}=V_A-C^2/{(2V_B^2)}$, while the first diagonal element of conditional matrix $\gamma _{A|B}$, and $V_{A|B}$ which represents conditional variance in amplitude quadrature, is given by

$$\begin{aligned} \begin{aligned} \gamma _{A|x_B}=\gamma _A-\sigma _{AB}(X\gamma _BX^{-1})^{MP}{\sigma _{AB}}^T \end{aligned}, \end{aligned}$$

(35)

where MP presents the Moore-Penrose matrix inverse; $\gamma _A$, $\gamma _B$ and $\sigma _{AB}$ refer to submatrices of the covariance matrix $\gamma _{AB}$ by decomposition, namely

$$\begin{aligned} \begin{aligned} \gamma _{A|B}= \begin{pmatrix} \frac{\sqrt{V_M+1}(1-{\eta }T_c{C_1}^2)}{{\eta }T_c(V_M+1+\chi _{tot})} &{} 0 \\ 0 &{} \sqrt{V_M+1} \end{pmatrix} , \end{aligned} \end{aligned}$$

(36)

where X and $\gamma _{AB}$ can be obtained in Ref. [48].

Lossy information available for Eve can be obtained by

$$\begin{aligned} \begin{aligned} \chi _{BE}=S(\rho _E)-S(\rho _E^{x_B}) \end{aligned}, \end{aligned}$$

(37)

where $S(\rho )$ is the Von Neumann entropy of the quantum state $\rho$. The calculation of symplectic eigenvalues of covariance matrix $\gamma$ is applied to evaluate entropy for an n-mode Gaussian state describing $\rho$ as follows:

$$\begin{aligned} \begin{aligned} S(\rho )=\sum _{i=1}^2G\left( \frac{(\lambda _i-1)}{2}\right) -G\left( \frac{(\lambda _3-1)}{2}\right) \end{aligned}, \end{aligned}$$

(38)

where G(x) can also be obtained in Ref. [48].