Skip to main content

Advertisement

Springer Nature Link
Log in

Characterizing the average coherence via a broad class of informationally complete symmetric measurements

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

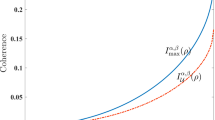
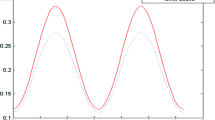
Abstract

Coherence is a foundational feature of quantum mechanics and is increasingly becoming recognized as a key resource for quantum theory. Based on coherence measure, our goal in this work is to evaluate the average coherence of a quantum state with respect to a broad class of informationally complete symmetric measurements by using Wigner–Yanase skew information. In addition, the relationship between these average coherence is also clearly established according to the different efficiency parameters. These results may further enrich the properties of average coherence.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

The data sets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

  1. Mandel, L., Wolf, E.: Optical Coherence and Quantum Optics. Cambridge University Press, Cambridge (1995)

    Book  Google Scholar 

  2. London, F., London, H.: The electromagnetic equations of the supraconductor. Proc. R. Soc. A 149, 71 (1935)

    ADS  MATH  Google Scholar 

  3. Ćwikliński, P., Studziński, M., Horodecki, M., Oppenheim, J.: Limitations on the evolution of quantum coherences: towards fully quantum second laws of thermodynamics. Phys. Rev. Lett. 115, 210403 (2015)

    Article  ADS  Google Scholar 

  4. Baumgratz, T., Cramer, M., Plenio, M.B.: Quantifying coherence. Phys. Rev. Lett. 113, 140401 (2014)

    Article  ADS  Google Scholar 

  5. Streltsov, A., Singh, U., Dhar, H.S., Bera, M.N., Adesso, G.: Measuring quantum coherence with entanglement. Phys. Rev. Lett. 115, 020403 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  6. Winter, A., Yang, D.: Operational resource theory of coherence. Phys. Rev. Lett. 116, 120404 (2016)

    Article  ADS  Google Scholar 

  7. Yu, X.D., Zhang, D.J., Xu, G.F., Tong, D.M.: Alternative framework for quantifying coherence. Phys. Rev. A 94, 060302(R) (2016)

    Article  ADS  Google Scholar 

  8. Chen, B., Fei, S.M.: Notes on modified trace distance measure of coherence. Quantum Inf. Process. 17, 107 (2018)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  9. Rastegin, A.E.: Quantum-coherence quantifiers based on the Tsallis relative \(\alpha \) entropies. Phys. Rev. A 93, 032136 (2016)

    Article  ADS  Google Scholar 

  10. Napoli, C.C., Bromley, T.R., Cianciaruso, M., Piani, M., Johnston, N., Adesso, G.: Robustness of coherence: an operational and observable measure of quantum coherence. Phys. Rev. Lett. 116, 150502 (2016)

    Article  ADS  Google Scholar 

  11. Luo, S., Sun, Y.Y.: Quantum coherence versus quantum uncertainty. Phys. Rev. A 96, 022130 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  12. Wigner, E.P., Yanase, M.M.: Information contents of distributions. Proc. Natl. Acad. Sci. U.S.A. 49, 910 (1963)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  13. Luo, S., Sun, Y.: Average versus maximal coherence. Phys. Lett. A 383, 2869–2873 (2019)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  14. Schwinger, J.: Unitary operator bases. Proc. Nat. 46, 570 (1960)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  15. Wootters, W.K., Fields, B.D.: Optimal state-determination by mutually unbiased measurement. Ann. Phys. 191, 2 (1989)

    Article  MathSciNet  Google Scholar 

  16. Durt, T., Englert, B.G., Bengtsson, I., Życzkowski, K.: On mutually unbiased bases. Int. J. Quantum Inf. 8, 535 (2010)

    Article  MATH  Google Scholar 

  17. Kalev, A., Gour, G.: Mutually unbiased measurements in finite dimensions. New J. Phys. 16, 053038 (2014)

    Article  ADS  MATH  Google Scholar 

  18. Scott, A.J., Grassl, M.: Symmetric informationally complete positive-operator-valued measures: a new computer study. J. Math. Phys. 51, 042203 (2010)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  19. Appleby, D.M.: Symmetric informationally complete measurements of arbitrary rank. Opt. Spectrosc. 103, 416 (2007)

    Article  ADS  Google Scholar 

  20. Gour, G., Kalev, A.: Construction of all general symmetric informationally complete measurements. J. Phys. A: Math. Theor. 47, 335302 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  21. Wootters, W.K., Fields, B.D.: Optimal state-determination by mutually unbiased measurements. Ann. Phys. 191, 363 (1989)

    Article  ADS  MathSciNet  Google Scholar 

  22. Chen, B., Ma, T., Fei, S.M.: Entanglement detection using mutually unbiased measurements. Phys. Rev. A 89, 064302 (2014)

    Article  ADS  Google Scholar 

  23. Liu, L., Gao, T., Yan, F.: Separability criteria via sets of mutually unbiased measurements. Sci. Rep. 5, 13138 (2015)

    Article  ADS  Google Scholar 

  24. Wiesniak, M., Paterek, T., Zeilinger, A.: Entanglement in mutually unbiased bases. New J. Phys. 13, 053047 (2011)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  25. Désignolle, S., Skrzypczyk, P.P., Fröwis, F., Brunner, N.: Quantifying measurement incompatibility of mutually unbiased bases. Phys. Rev. Lett. 122, 050402 (2019)

    Article  ADS  Google Scholar 

  26. Czartowski, J., Goyeneche, D., Zyczkowski, K.: Entanglement properties of multipartite information- ally complete quantum measurements. J. Phys. A: Math. Theor. 51, 305302 (2018)

    Article  MATH  Google Scholar 

  27. Shen, S.Q., Li, M., Li-Jost, X., Fei, S.M.: Improved separability criteria via some classes of measurements. Quantum Inf. Process. 17, 111 (2018)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  28. Shang, J.W., Asadian, A., Zhu, H.J.: Enhanced entanglement criterion via symmetric informationally complete measurements. Phys. Rev. A 98, 022309 (2018)

    Article  ADS  Google Scholar 

  29. Xi, Y., Zheng, Z.J., Zhu, C.J.: Entanglement detection via general SIC-POVMs. Quantum Inf. Process. 15, 5119 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  30. Bae, J., Hiesmayr, B.C., McNulty, D.: Linking entanglement detection and state tomography via quantum 2-designs. New J. Phys. 21, 013012 (2019)

    Article  ADS  Google Scholar 

  31. Katarzyna, S.: All class of informationally complete symmetric measurements in finite dimensions. Phys. Rev. A 105, 042209 (2022)

    Article  Google Scholar 

  32. Lieb, E.H.: Convex trace functions and the Wigner-Yanase-Dyson conjecture. Adv. Math. 11, 267 (1973)

    Article  MathSciNet  MATH  Google Scholar 

  33. Li, D., Li, X., Wang, F., et al.: Uncertainty relation of mixed states by means of Wigner-Yanase-Dyson information. Phys. Rev. A 79, 052106 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  34. Yanagi, K.: Uncertainty relation on Wigner-Yanase-Dyson skew information. J. Math. Anal. Appl. 12, 365 (2010)

    MathSciNet  MATH  Google Scholar 

  35. Li, X., Li, D., Huang, H., et al.: Averaged Wigner-Yanase-Dyson information as a quantum uncertainty measure. Eur. Phys. J. D 64, 147 (2011)

    Article  ADS  Google Scholar 

  36. Luo, S.: Brukner-Zeilinger invariant information. Theor. Math. Phys. 15, 693 (2015)

    MathSciNet  MATH  Google Scholar 

  37. Lostaglio, M., Jennings, D., Rudolph, T.: Description of quantum coherence in thermodynamic processes requires constraints beyond free energy. Nat. Commun. 6, 6383 (2015)

    Article  ADS  Google Scholar 

  38. Kammerlander, P., Anders, J.: Coherence and measurement in quantum thermodynamics. Sci. Rep. 6, 22174 (2016)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work is supported by National Science Foundation of Sichuan Province (No. 2022NSFSC0534), the Central Guidance on Local Science and Technology Development Fund of Sichuan Province (No. 22ZYZYTS0064), the Chengdu Key Research and Development Support Program (No. 2021-YF09-0016-GX), the key project of Sichuan Normal University (No. XKZX-02).

Author information

Authors and Affiliations

  1. School of Science, Xihua University, Chengdu, 610039, China

    Liang Tang

  2. School of Mathematical Sciences, Sichuan Normal University, Chengdu, 610066, China

    Fan Wu

  3. Institute of Intelligent Information and Quantum Information, Sichuan Normal University, Chengdu, 610066, China

    Liang Tang & Fan Wu

Authors
  1. Liang Tang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Fan Wu
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

In fact, all of the authors’ contributions to this paper are important. The specific contributions are as follows. The first author played a major role in the conceptualization and writing of the article. The second author worked mainly on the overall framework and language of the article.

Corresponding author

Correspondence to Liang Tang.

Ethics declarations

Conflict of interest

No potential conflict of interest was reported by the authors. All authors of this manuscript have read and approved the final version submitted and contents of this manuscript have not been copyrighted or published previously and are not under consideration for publication elsewhere.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tang, L., Wu, F. Characterizing the average coherence via a broad class of informationally complete symmetric measurements. Quantum Inf Process 22, 65 (2023). https://doi.org/10.1007/s11128-022-03822-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-022-03822-0

Keywords