Enhancing the controller’s power in teleporting an arbitrary two-qubit state by using the asymmetry of the four-qubit cluster state

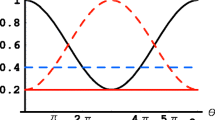
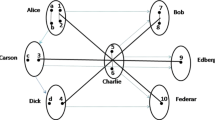
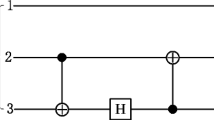
Abstract

In this paper, we use a quantum channel that is the product of two states, the four-qubit cluster state and the three-qubit partially entangled state. This quantum channel is used as a channel in the two controlled teleportation protocols of an arbitrary two-qubit state. When the controller cooperates, both of these protocols are perfect, i.e., the total success probability and the quantum fidelity of the state received by the receiver are equal to 1. In the two controlled teleportation protocols, the number of qubits held by the controller is the same. However, depending on how the qubits in the channel are distributed to the controller, the controller’s power may be entirely in or below the quantum domain. Thus, the controller’s power is guaranteed when the qubits in the quantum channel are correctly distributed. On the other hand, we also show that the controller’s power depends on the entanglement of the qubits that the controller holds with the rest of the qubits in the channel.

Appendix

This appendix presents a mathematical description of the steps performed in the two protocols.

Protocol 1 According to the distribution of qubits of the cluster state (3) of protocol 1, we can write the expression of this cluster state as follows

$$\begin{aligned} \left| C_{4}\right\rangle _{A_{1}B_{1}C_{1}C_{2}}=\frac{1}{2} \sum \limits _{m,n=0}^{1}\left( -1\right) ^{mn}\left| mn\right\rangle _{A_{1}B_{1}}\left| mn\right\rangle _{C_{1}C_{2}}. \end{aligned}$$

(30)

The results of protocol 1 do not depend on whether the sender Alice first performs the Bell measurements or the controller Charlie first performs the measurements because these measurements are independent of each other. To give the expression of state (30) a simple form, we assume that, the first the controller Charlie applies the operator $CZ_{C_{1}C_{2}}$ to the pair of qubits $C_{1}$ and $C_{2},$ then equation (30) becomes

$$\begin{aligned}{} & {} \left| C_{41}\right\rangle _{A_{1}B_{1}C_{1}C_{2}}=CZ_{C_{1}C_{2}}\left| C_{4}\right\rangle _{A_{1}B_{1}C_{1}C_{2}}~ \nonumber \\{} & {} \quad =\frac{1}{2}\sum \limits _{m,n=0}^{1}\left( -1\right) ^{mn}\left| mn\right\rangle _{A_{1}B_{1}}\left( CZ_{C_{1}C_{2}}\left| mn\right\rangle _{C_{1}C_{2}}\right) \\{} & {} \quad =\frac{1}{2}\sum \limits _{m,n=0}^{1}\left| mn\right\rangle _{A_{1}B_{1}}\left| mn\right\rangle _{C_{1}C_{2}}.~ \nonumber \end{aligned}$$

(31)

Using the Bell state formulas

$$\begin{aligned} \left| B_{mn}\right\rangle =\frac{1}{\sqrt{2}}\sum \limits _{i=0}^{1} \left( -1\right) ^{mi}\left| i,n\oplus i\right\rangle , \end{aligned}$$

(32)

then state (31) is rewritten as follows

$$\begin{aligned} \left| C_{41}\right\rangle _{A_{1}B_{1}C_{1}C_{2}}=\frac{1}{2} \sum \limits _{m,n=0}^{1}\left| B_{mn}\right\rangle _{A_{1}B_{1}}\left| B_{mn}\right\rangle _{C_{1}C_{2}} \end{aligned}$$

(33)

and state (4) becomes

$$\begin{aligned} \left| G\left( \theta \right) \right\rangle _{A_{2}B_{2}C_{3}}=\sum \limits _{q=0}^{1}\left| B_{q0}\right\rangle _{A_{2}B_{2}}\left| \widetilde{q}\right\rangle _{C_{3}}, \end{aligned}$$

(34)

in there

$$\begin{aligned} \left| \widetilde{0}\right\rangle _{C_{3}}=\frac{1}{2}\left( \left| 0\right\rangle +\cos \theta \left| 0\right\rangle -\sin \theta \left| 1\right\rangle \right) _{C_{3}}, \left| \widetilde{1}\right\rangle _{C_{3}}=\frac{1}{2}\left( \left| 0\right\rangle -\cos \theta \left| 0\right\rangle +\sin \theta \left| 1\right\rangle \right) _{C_{3}}. \nonumber \\ \end{aligned}$$

(35)

The general state of the two qubits to be teleported (1) can be rewritten as

$$\begin{aligned} {\left| \psi \right\rangle _{XY}=}\sum \limits _{a,b=0}^{1} \alpha _{ab}\left| a,b\right\rangle _{XY}\!, \end{aligned}$$

(36)

in there

$$\begin{aligned} \alpha _{00}=x,\alpha _{01}=ye^{i\varphi _{1}},\alpha _{10}=ze^{i\varphi _{2}},\alpha _{11}=te^{i\varphi _{3}}. \end{aligned}$$

(37)

Then, the product state of the two qubits to be teleported and the quantum channel of protocol 1 can be expressed as

$$\begin{aligned}{} & {} \left| T_{1}\right\rangle ={\left| \psi \right\rangle _{XY}} \left| C_{41}\right\rangle _{A_{1}B_{1}C_{1}C_{2}}\left| G\left( \theta \right) \right\rangle _{A_{2}B_{2}C_{3}} ~ \nonumber \\{} & {} \quad =\frac{1}{2} \sum \limits _{a,b=0}^{1}\sum \limits _{m,n=0}^{1}\sum \limits _{q=0}^{1}\alpha _{ab}\left| a,b\right\rangle _{XY}\left| B_{mn}\right\rangle _{A_{1}B_{1}}\left| B_{q0}\right\rangle _{A_{2}B_{2}}\left| B_{mm}\right\rangle _{C_{1}C_{2}}\left| \widetilde{q}\right\rangle _{C_{3}}.\nonumber \\{} & {} \end{aligned}$$

(38)

Using the Bell state formula (32) and the inverse transformation of the form

$$\begin{aligned} \left| mn\right\rangle =\frac{1}{\sqrt{2}}\sum \limits _{i=0}^{1}\left( -1\right) ^{mi}\left| B_{i,m\oplus n}\right\rangle , \end{aligned}$$

(39)

the equation (38) is rewritten as

$$\begin{aligned} \left| T_{1}\right\rangle =\frac{1}{8}\sum \limits _{i,j=0}^{1}\sum \limits _{k,l=0}^{1}\sum \limits _{m,n=0}^{1}\sum \limits _{q=0}^{1}\sum \limits _{a,b=0}^{1}\alpha _{ab}\left( -1\right) ^{mj\oplus ql\oplus a\left( m\oplus i\right) \oplus b\left( k\oplus q\right) } ~ \nonumber \\ \left| B_{ij}\right\rangle _{XA_{1}}\left| B_{kl}\right\rangle _{YA_{2}}\left| B_{mn}\right\rangle _{C_{1}C_{2}}\left| \widetilde{q}\right\rangle _{C_{3}}\left| n\oplus a\oplus j,l\oplus b\right\rangle _{B_{1}B_{2}}. \end{aligned}$$

(40)

When the controller Charlie applies the rotation gate $R\left( -\theta \right)$ to qubit $C_{3},$ equation (35) becomes

$$\begin{aligned} \left| \widetilde{0}\right\rangle _{C_{3}}=\left( \cos \theta /2\right) \left| 0\right\rangle _{C_{3}};\left| \widetilde{1}\right\rangle _{C_{3}}=\left( \sin \theta /2\right) \left| 0\right\rangle _{C_{3}}. \end{aligned}$$

(41)

After the controller Charlie applies the rotation gate $R\left( -\theta \right)$ to qubit $C_{3}$, the state (40) becomes

$$\begin{aligned} \left| T_{1}\right\rangle =\frac{1}{8}\sum \limits _{i,j=0}^{1}\sum \limits _{k,l=0}^{1}\sum \limits _{m,n=0}^{1}\sum \limits _{p=0}^{1}\left( -1\right) ^{mj\oplus pl}\beta _{p}\left| B_{ij}\right\rangle _{XA_{1}}\left| B_{kl}\right\rangle _{YA_{2}}\left| B_{mn}\right\rangle _{C_{1}C_{2}}\left| p\right\rangle _{C_{3}}\nonumber \\ \left( \sum \limits _{a,b=0}^{1}\alpha _{ab}\left( -1\right) ^{a\left( m\oplus i\right) \oplus b\left( k\oplus p\right) }\left| n\oplus a\oplus j,l\oplus b\right\rangle _{B_{1}B_{2}}\right) ,\nonumber \\{} & {} \end{aligned}$$

(42)

in there $\beta _{0}=\cos \theta /2$, $\beta _{1}=\sin \theta /2.$

It is clear from equation (42) that if Alice makes two Bell-state measurements on the pairs of qubits $\left( XA_{1}\right)$, $\left( YA_{2}\right)$ with outcomes $\left\{ ij\right\}$, $\left\{ kl\right\}$ corresponding to finding $\left| B_{ij}\right\rangle _{XA_{1}}$, $\left| B_{kl}\right\rangle _{YA_{2}}$. Charlie makes Bell-state measurement on the pair of qubits $\left( C_{1}C_{2}\right)$ with outcomes $\left\{ mn\right\}$ corresponding to finding $\left| B_{mn}\right\rangle _{C_{1}C_{2}}$. Charlie measures qubit $C_{3}$ in the computational basis $\left\{ \left| 0\right\rangle _{C_{3}},~\left| 1\right\rangle _{C_{3}}\right\}$ with an outcome $\left\{ p\right\}$ corresponding to finding $\left| p\right\rangle _{C_{3}}$, then the state of Bob’s qubits $B_{1}$ and $B_{2}$, up to a global phase factor $\left( -1\right) ^{mj\oplus pl}$, is projected onto

$$\begin{aligned} \left| \psi _{1}\right\rangle _{XY}=\sum \limits _{a,b=0}^{1}\alpha _{ab}\left( -1\right) ^{a\left( m\oplus i\right) \oplus b\left( k\oplus q\right) }\left| n\oplus j\oplus a,l\oplus b\right\rangle _{B_{1}B_{2}}. \end{aligned}$$

(43)

The measurement results of Alice $\left( \left\{ ij\right\} \text {, }\left\{ kl\right\} \right)$ and Charlie $\left( \left\{ mn\right\} \text {, }\left\{ p\right\} \right)$ are sent to the receiver Bob over the classical communication channel. To transform state (43) to the original state that Alice wants to send, equation (1), Bob acts on qubits $B_{1}$ and $B_{2}$, the unitary recovery operator, which is determined by the following expression

$$\begin{aligned} U_{ijklmnp}=R_{B_{1}}\otimes R_{B_{2}}=\left( Z^{m\oplus i}.X^{j\oplus n}\right) _{B_{1}}\otimes \left( Z^{k\oplus p}.X^{l}\right) _{B_{2}}. \end{aligned}$$

(44)

The probability of Alice and Charlie’s respective measurements is

$$\begin{aligned} P_{ijklmnp}=\left| \frac{\beta _{p}}{8}\right| ^{2}=\frac{\beta _{p}^{2}}{64}. \end{aligned}$$

(45)

The total success probability of protocol 1 is

$$\begin{aligned}{} & {} P_{1}=\sum \limits _{i,j=0}^{1}\sum \limits _{k,l=0}^{1}\sum \limits _{m,n=0}^{1} \sum \limits _{p=0}^{1}P_{ijklmnp} ~ \nonumber \\{} & {} \quad =\sum \limits _{i,j=0}^{1}\sum \limits _{k,l=0}^{1}\sum \limits _{m,n=0}^{1}\sum \limits _{p=0}^{1}\frac{\beta _{p}^{2}}{64}=64\frac{\cos ^{2}\theta /2+\sin ^{2}\theta /2}{64}=1. \end{aligned}$$

(46)

Protocol 2 According to the distribution of qubits of the cluster state in equation (3) of protocol 2, we can write this cluster state as follows

$$\begin{aligned} \left| C_{42}\right\rangle _{A_{1}C_{1}B_{1}C_{2}}=\frac{1}{\sqrt{2}} \sum \limits _{m=0}^{1}\left| B_{m0}\right\rangle _{A_{1}C_{1}}\left| mm\right\rangle _{B_{1}C_{2}}. \end{aligned}$$

(47)

State (4) still has the same form as equation (34) in protocol 1. Then, the product state of the two qubits to be teleported and the quantum channel of protocol 2 can be expressed as

$$\begin{aligned}{} & {} \left| T_{2}\right\rangle ={\left| \psi \right\rangle _{XY}} \left| C_{42}\right\rangle _{A_{1}C_{1}B_{1}C_{2}}\left| G\left( \theta \right) \right\rangle _{A_{2}B_{2}C_{3}}~ \nonumber \\{} & {} \quad =\frac{1}{\sqrt{2}} \sum \limits _{a,b=0}^{1}\sum \limits _{m=0}^{1}\sum \limits _{q=0}^{1}\alpha _{ab}\left| a,b\right\rangle _{XY}\left| B_{m0}\right\rangle _{A_{1}C_{1}}\left| B_{q0}\right\rangle _{A_{2}B_{2}}\left| mm\right\rangle _{B_{1}C_{2}}\left| \widetilde{q}\right\rangle _{C_{3}}.\nonumber \\{} & {} \end{aligned}$$

(48)

Using the formula for the Bell state (32) and the inverse transformation (39), the state (48) can be rewritten as:

$$\begin{aligned} \left| T_{2}\right\rangle =\frac{1}{4\sqrt{2}}\sum \limits _{i,j=0}^{1} \sum \limits _{k,l=0}^{1}\sum \limits _{m=0}^{1}\sum \limits _{q=0}^{1}\sum \limits _{a,b=0}^{1}\alpha _{ab}\left( -1\right) ^{mj\oplus ql\oplus a\left( m\oplus i\right) \oplus b\left( k\oplus q\right) } ~ \nonumber \\ \left| B_{ij}\right\rangle _{XA_{1}}\left| B_{kl}\right\rangle _{YA_{2}}\left| mm\right\rangle _{B_{1}C_{2}}\left| \widetilde{q}\right\rangle _{C_{3}}\left| a\oplus j,l\oplus b\right\rangle _{C_{1}B_{2}}. \end{aligned}$$

(49)

After the controller Charlie applies the rotation gate $R\left( \theta \right)$ to qubit $C_{3}$, the state (49) becomes

$$\begin{aligned} \left| T_{2}\right\rangle =\frac{1}{4\sqrt{2}}\sum \limits _{i,j=0}^{1} \sum \limits _{k,l=0}^{1}\sum \limits _{m=0}^{1}\sum \limits _{p=0}^{1}\left( -1\right) ^{mj\oplus pl}\beta _{p}\left| B_{ij}\right\rangle _{XA_{1}}\left| B_{kl}\right\rangle _{YA_{2}}\left| mm\right\rangle _{B_{1}C_{2}}\left| p\right\rangle _{C_{3}} ~ \nonumber \\ \left( \sum \limits _{a,b=0}^{1}\alpha _{ab}\left( -1\right) ^{a\left( m\oplus i\right) \oplus b\left( k\oplus p\right) }\left| a\oplus j,l\oplus b\right\rangle _{C_{1}B_{2}}\right) .~ \nonumber \\{} & {} \end{aligned}$$

(50)

It is now clear from equation (50) that if Alice makes two Bell-state measurements on the pairs of qubits $\left( XA_{1}\right)$, $\left( YA_{2}\right)$ with outcomes $\left\{ ij\right\}$, $\left\{ kl\right\}$ corresponding to finding $\left| B_{ij}\right\rangle _{XA_{1}}$, $\left| B_{kl}\right\rangle _{YA_{2}}$. Charlie measures qubits $B_{1},$ $C_{2}$ and qubit $C_{3}$ on a computational basis $\left\{ \left| 0\right\rangle ,\left| 1\right\rangle \right\}$ with an outcome $\left\{ mn\right\} \left( n=m\right)$ and $\left\{ p\right\}$ corresponding to finding $\left| mm\right\rangle _{B_{1}C_{2}}$ and $\left| p\right\rangle _{C_{3}}$, then the state of Bob’s qubits $C_{1}$ and $B_{2}$, up to a global phase factor $\left( -1\right) ^{mj\oplus pl}$, is projected onto

$$\begin{aligned} \left| \psi _{2}\right\rangle _{XY}=\sum \limits _{a,b=0}^{1}\alpha _{ab}\left( -1\right) ^{a\left( m\oplus i\right) \oplus b\left( k\oplus q\right) }\left| j\oplus a,l\oplus b\right\rangle _{C_{1}B_{2}}. \end{aligned}$$

(51)

The measurement results of Alice $\left( \left\{ ij\right\} \text {, }\left\{ kl\right\} \right)$ and Charlie $\left( \left\{ mn\right\} \text {, }\left\{ p\right\} \right)$ are sent to the receiver Bob over the classical communication channel. To transform state (51) to the original state that Alice wants to send, equation (1), Bob acts on qubits $C_{1}$ and $B_{2}$ the unitary recovery operator, which is determined by the following expression

$$\begin{aligned} U_{ijklmp}=R_{C_{1}}\otimes R_{B_{2}}=\left( Z^{m\oplus i}.X^{j}\right) _{C_{1}} \otimes \left( Z^{k\oplus p}.X^{l}\right) _{B_{2}}. \end{aligned}$$

(52)

The probability of Alice and Charlie’s respective measurements is

$$\begin{aligned} P_{ijklmp}=\left| \frac{\beta _{p}}{4\sqrt{2}}\right| ^{2}=\frac{ \beta _{p}^{2}}{32}. \end{aligned}$$

(53)

The total success probability of protocol 2 is

$$\begin{aligned}{} & {} P_{2}=\sum \limits _{i,j=0}^{1}\sum \limits _{k,l=0}^{1}\sum \limits _{m=0}^{1} \sum \limits _{p=0}^{1}P_{ijklmp} ~ \nonumber \\{} & {} \quad =\sum \limits _{i,j=0}^{1}\sum \limits _{k,l=0}^{1}\sum \limits _{m=0}^{1}\sum \limits _{p=0}^{1}\frac{\beta _{p}^{2}}{32}=32\frac{\cos ^{2}\theta /2+\sin ^{2}\theta /2}{32}=1. \end{aligned}$$

(54)