Skip to main content
SpringerLink
Log in

Variable ansatz applied to spectral operator decomposition in a physical superconducting quantum device

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

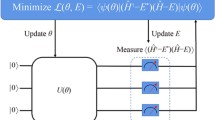
Abstract

Several techniques for extracting excited states from the Hamiltonian operator have been studied in recent years. This analysis is essential in areas such as Molecular Chemistry and other branches of Quantum Physics, especially those related to optical spectra and chemical reaction processes. Moreover, the knowledge of the operators’ spectrum is required in other fields outside the Physics domains, since there are problems related to graph connectivity and principal component analysis which require a knowledge of, if not all, some important values of the operator spectrum. For those cases, part of the results clarifies that the eigenstate deflation can be used as a tool to extract the excited states. In consonance with these properties, we present a framework to perform the spectral decomposition for any dimension operator in a procedure based on the Householder reflections and unconstrained optimization using a meta-heuristic technique named Differential Evolution. The technique is discussed through examples and implemented in the superconducting real quantum device from IBM Quantum, whose results (without neglecting the system decoherence) follows the pattern expected for the respective models. We conclude our analysis, showing that the proposed framework presents encouraging results to exploit other scenarios in this field.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Data availability

Data will be made available on reasonable request

References

  1. Deutsch, D.: Quantum theory, the church-turing principle and the universal quantum computer. Proc. Royal Soc. Lond. 400, 97–117 (1985)

    ADS  MathSciNet  MATH  Google Scholar 

  2. Sipser, M.: Introduction to the Theory of Computation. Cengage Learning, Boston (2007)

    MATH  Google Scholar 

  3. Deutsch, D., Jozsa, R.: Rapid solution of problems by quantum computation. Proc. Royal Soc. Lond. 439, 553–558 (1992)

    ADS  MathSciNet  MATH  Google Scholar 

  4. Shor, P.: Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput. 29, 1484–1509 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  5. Ladd, T.D., Jelezko, F., Laflamme, R., Nakamura, Y., Monroe, C., O’Brien, J.L.: Quantum computers. Nature 464, 45–53 (2010)

    Article  ADS  Google Scholar 

  6. Preskill, J.: Quantum computing in the NISQ era and beyond. Quantum 2(79), 1–20 (2018)

    Google Scholar 

  7. Peruzzo, A., McClean, J., Shadbolt, P., Yung, M.-H., Zhou, X.-Q., Love, P.J., Aspuru-Guzik, A., O’Brien, J.L.: A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 4213 (2014)

    Article  ADS  Google Scholar 

  8. Cerezo, M., Arrasmith, A., Babbush, R., Benjamin, S.C., Endo, S., Fujii, K., McClean, J.R., Mitarai, K., Yuan, X., Cincio, L., Coles, P.J.: Variational quantum algorithm. Nat. Rev. Phys. 3(1), 625–644 (2021)

    Article  Google Scholar 

  9. Mermin, N.D.: Quantum Computer Science: An Introduction, 1st edn. Cambridge University Press, Cambridge (2007)

    Book  MATH  Google Scholar 

  10. Kitaev, A.Y.: Quantum measurements and the abelian stabilizer problem. arXiv:quant-ph/9511026 20(1), 101–106 (1995)

  11. Colless, J.I., Ramasesh, V.V., Dahlen, D., Blok, M.S., Kimchi-Schwartz, M.E., McClean, J.R., Carter, J., Jong, W.A., Siddiqi, I.: Computation of molecular spectra on a quantum processor with an error-resilient algorithm. Phys. Rev. X 8, 011021 (2018). https://doi.org/10.1103/PhysRevX.8.011021

    Article  Google Scholar 

  12. Higgott, O., Wang, D., Brierley, S.: Variational quantum computation of excited states. Quantum 3, 156 (2019). https://doi.org/10.22331/q-2019-07-01-156

    Article  Google Scholar 

  13. Jones, T., Endo, S., McArdle, S., Yuan, X., Benjamin, S.C.: Variational quantum algorithms for discovering Hamiltonian spectra. Phys. Rev. A 99, 062304 (2019). https://doi.org/10.1103/PhysRevA.99.062304

    Article  ADS  Google Scholar 

  14. Nakanishi, K.M., Mitarai, K., Fujii, K.: Subspace-search variational quantum Eigensolver for excited states. Phys. Rev. Res. 1, 033062 (2019). https://doi.org/10.1103/PhysRevResearch.1.033062

    Article  Google Scholar 

  15. Watkins, D.S.: Fundamentals of Matrix Computations. Wiley-Interscience, Hoboken (2002)

    Book  MATH  Google Scholar 

  16. MacDonald, J.K.L.: Successive approximations by the Rayleigh-ritz variation method. Phys. Rev. 43, 830–833 (1933)

    Article  ADS  MATH  Google Scholar 

  17. Koch, E.A.D.: Fundamentals in quantum algorithms: a tutorial series using qiskit continued (2020). arXiv:2008.10647

  18. McClean, J.R., Boixo, S., Smelyanskiy, V.N., Babbush, R., Neven, H.: Barren plateaus in quantum neural network training landscapes. Nat. Commun. 9(4812), 1–6 (2018)

    ADS  Google Scholar 

  19. Bhatnagar, S., Prasad, H.L., Prashanth, L.A.: Stochastic Recursive Algorithms for Optimization: Simultaneous Perturbation Methods. Springer, Berlin (2013)

    Book  MATH  Google Scholar 

  20. Hirokami, T., Maeda, Y., Tsukada, H.: Parameter estimation using simultaneous perturbation stochastic approximation. Electr. Eng. Jpn. 154(2), 30–3 (2006)

    Article  Google Scholar 

  21. Storn, R.M., Price, K.: Differential evolution—a simple and efficient heuristic for global optimizationover continuous spaces. J. Glob. Optim. 11, 341–359 (1997)

    Article  MATH  Google Scholar 

  22. Fiedler, P.M.: Algebraic connectivity of graphs. Czechoslov. Math. J. 23, 298–305 (1973)

    Article  MathSciNet  MATH  Google Scholar 

  23. Pothen, A., Simon, H.D., Liu, K.P.P.: Partitioning sparse matrices with eigenvectors of graphs. Report RNR-89-009—NASA Systems Division, 1–30 (1989)

  24. Bishop, C.M.: Pattern Recognition and Machine Learning, 1st edn. Springer, Cambridge (2006)

    MATH  Google Scholar 

  25. Qiskit: 27. Quantum Chemistry II: finding the Ground States of H2 and LiH—Part 3 (2020). https://www.youtube.com/watch?v=o4BAOKbcd3o Accessed 01 September 2020

  26. Kandala, A., Mezzacapo, A., Temme, K., Takita, M., Brink, M., Chow, J.M., Gambetta, J.M.: Hardware-efficient variational quantum Eigensolver for small molecules and quantum magnets. Nature 549(1), 242–246 (2017). https://doi.org/10.1038/nature23879

    Article  ADS  Google Scholar 

  27. Buhrman, H., Cleve, R., Watrous, J., Wolf, R.: Quantum fingerprinting. Phys. Rev. Lett. 87, 167902 (2001). https://doi.org/10.1103/PhysRevLett.87.167902

    Article  ADS  Google Scholar 

  28. Haferkamp, J., Faist, P., Kothakonda, N.B.T., Eisert, J., Yunger Halpern, N.: Linear growth of quantum circuit complexity. Nat. Phys. 18(5), 528–532 (2022)

    Article  Google Scholar 

Download references

Acknowledgements

We thank to IBM for access to superconducting quantum devices through the both Quantum Researchers Program and Qiskit SDK. Finally, we thank the Quantum Computing and Optimization group of the UNILA for the suggestions and discussions.

Author information

Author notes

  1. Anton Simen Albino, Rodrigo Bloot, and Raphael F. I. Gomes have contributed equally to this work.

Authors and Affiliations

  1. Kipu Quantum, Roonstraße 23a, 76137, Karlsruhe, Germany

    Anton Simen Albino

  2. Federal University for Latin American Integration, Foz do Iguaçu, Brazil

    Anton Simen Albino, Rodrigo Bloot & Raphael F. I. Gomes

Authors
  1. Anton Simen Albino
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rodrigo Bloot
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Raphael F. I. Gomes
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors worked equally on the paper.

Corresponding author

Correspondence to Rodrigo Bloot.

Ethics declarations

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Albino, A.S., Bloot, R. & Gomes, R.F.I. Variable ansatz applied to spectral operator decomposition in a physical superconducting quantum device. Quantum Inf Process 22, 233 (2023). https://doi.org/10.1007/s11128-023-04001-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-023-04001-5

Keywords

Search

Navigation