A receiver for quadrature/polarization modulated quantum coherent states in photonic communications employing the Naimark extension

Abstract

This work deals with the derivation of a receiver structure for the quantum detection of information-carrying coherent states used in photonic communications systems, that employ the degrees of freedom of both the complex amplitude and the state of polarization in the quantum state, producing a high dimensional modulation in the form of a constellation of quantum composite coherent states to be transmitted in the optical channel. Our receiver is based on the extension of the positive operator value measurements (POVM) in the constellation Hilbert space, towards projective measurements in a larger Hilbert space. Starting from the measurement vectors obtained from an optimum detection/discrimination strategy-the square root method (SRM) in our case-, and basing our analysis on the Naimark extension, we present a procedure for building those projectors for a received modulation format of composite coherent states. We analytically derive the orthogonal and idempotent projectors, arriving at closer form expressions for the considered modulation format, their decomposition in unitary rotations, and suggest a receiver configuration for its physical realization. Finally, an error probability analysis of our modulation formats is presented.

Appendices

Appendix 1: Composite quantum coherent states

In a scalar constellation of K symbols, the quantum state corresponding to its k-th point is represented by a single-mode ket in Dirac's notation: $\left|{\gamma }_{k}\right.>$, $k=\mathrm{0,1},\dots , K-1$ in a Hilbert space ${\mathcal{H}}_{0}$ of dimension dim(${\mathcal{H}}_{0}$); the state matrix is defined as:

$${\varvec{\Gamma}}=\left[\left|{\gamma }_{0}\right.> \left|{\gamma }_{1}\right.> \dots \left|{\gamma }_{K-1}\right.>\right]$$

(A1.1)

Multidimensional modulation formats must be formulated as vector modulations of order N, and we need a composite Hilbert space ${\mathcal{H}}_{C}$ with dimension dim(${\mathcal{H}}_{C}$) = [dim(${\mathcal{H}}_{0}$)]^N, and each composite state of the constellation $\left|{\gamma }_{k}\right.>$ in Eq. (1) is itself given by the N-fold tensor product:

$$ \left| {\gamma_{k} } \right. > = \left| {\gamma_{k, 0} } \right. > \otimes \left| {\gamma_{k, 1} } \right. > \otimes \cdots \otimes \left| {\gamma_{k, N - 1} } \right. > , k = 0,1, \ldots , K - 1 $$

(A1.2)

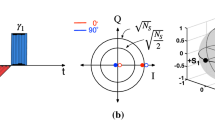
which is called an N-mode state; in M-ary modulation formats, the original Hilbert space ${\mathcal{H}}_{0}$ has dimension dim(${\mathcal{H}}_{0}$) = 2, corresponding to the in-phase (I) and quadrature (Q) components of a single polarization mode, as represented by N = 2 original states in Eq. (12):

$$\left|{\gamma }_{k, 0}\right.>=\left[\begin{array}{c}{\gamma }_{k, 0, I}\\ {i\gamma }_{k, 0 ,Q} \end{array}\right]and \left|{\gamma }_{k, 1}\right.>=\left[\begin{array}{c}{\gamma }_{k, 1 ,I}\\ {i\gamma }_{k, 1, Q}\end{array}\right], k=\mathrm{0,1},\dots , K-1,i=\sqrt{-1}$$

(A1.3)

where the components ${\gamma }_{k, 0, I}$ and ${\gamma }_{k, 0 ,Q}$ are respectively the in-phase (I) and quadrature (Q) of one of the polarization components of the optical field (SOP "0"); and ${\gamma }_{k, 1 ,I}$ and ${\gamma }_{k, 1, Q}$ are the corresponding quadratures of the antipodal polarization component (SOP "1"); "0" / "1" can represent the horizontal / vertical, left-circular / right-circular or any two antipodal SOPs on the Poincaré sphere.

With the polarization degree of freedom, we then work in a twofold composite Hilbert space ${\mathcal{H}}_{C}$ of dimension dim(${\mathcal{H}}_{C}$) = 4, and, depending on the specific M-ary modulation format, the K states of the four-dimensional (4D) constellation $\left|{\gamma }_{k}\right.>$ are now given by tensor products from permutations of the elements of the following 4D modulation vector [78]:

$$ \left[ {\gamma_{k, 0, I} \;\;i\gamma_{k, 0,Q} \;\;\gamma_{k, 1 ,I} \;\;i\gamma_{k, 1, Q} } \right]^{T} , k = 0,1, \ldots , K - 1 $$

(A1.4)

In this work we develop our analysis for quantum coherent states $\left|\propto \right.>$, expanded into a Fock state (number-state) basis $\left|n\right.> , n=0,\dots ,\infty$ [79]:

$$\left|\propto \right.>=\mathrm{exp}(-\frac{1}{2}{\left|\propto \right|}^{2})\sum_{n=0}^{\infty }\frac{{\propto }^{n}}{\sqrt{n!}}\left|n>\right.$$

(A1.5)

where ${\left|\propto \right|}^{2}$ is the average number of photons ${N}_{s}$ in the state $\left|\propto \right.>$.

For the case of pure coherent states, the inner product of a couple of states is calculated as:

$$<{\gamma }_{k}\left|{\gamma }_{l}\right.> =\mathrm{exp}\left[-\frac{1}{2}\left({\left|{\gamma }_{k}\right|}^{2}+{\left|{\gamma }_{l}\right|}^{2}-{2{\gamma }_{k}}^{*}{\gamma }_{l}\right)\right]$$

(A1.6)

and the absolute value of the degree of superposition of a coherent state of average number of photons ${{N}_{s}=\left|\Delta \right|}^{2}$, with vacuum $\left|0\right.>$:

$$\left|X\right|=<\Delta \left|0\right.>=exp(-{N}_{s}/2)$$

(A1.7)

Finally, for the N-mode tensor states of Eq. (3), the overlap is computed by the rule [7, 25]:

$$ \left\langle {\gamma_{k} \left| {\gamma_{l} } \right.} \right\rangle = \mathop \prod \limits_{m = 0}^{N - 1} \left\langle {\gamma_{k,m} \left| {\gamma_{l,m} } \right.} \right\rangle = \left\langle {\gamma_{k,0} \left| {\gamma_{l,0} } \right.} \right\rangle \left\langle {\gamma_{k,1} \left| {\gamma_{l,1} } \right.} \right\rangle \ldots \left\langle {\gamma_{k,N - 1} \left| {\gamma_{l,N - 1} } \right.} \right\rangle , k = 0,1, \ldots ,K - 1 $$

(A1.8)

Appendix 2: Quantum measurement vectors

Our aim is to construct a POVM with measurement vectors $\left|{\mu }_{k}>\right.$ optimized to distinguish between a set of K pure states $\left|{\upgamma }_{k}\right.>$ that span a subspace ${\mathcal{U}\subseteq \mathcal{H}}_{C}$; a convenient approach is to find a collection of vectors $\left|{\mu }_{k}>\in \mathcal{U}\right.$ that are “closest” to the original states $\left|{\upgamma }_{k}\right.>,$ in the least-squares sense, such that the measurement consists of K rank-one POVMs of the form ${\widehat{\Pi }}_{k}=\left|{\mu }_{k}>\right.<{\mu }_{k}|, k=0,...,K-1$ [18, 80].

The SRM method is based on the "measurement matrix" $\pmb{\mathcal{M}}$ whose elements $\left|{\mu }_{k}>, \right.$ are the measurement vectors

$$ \pmb{\mathcal{M}}=[\left|{\mu }_{0}> \right.\left|{\mu }_{1}> ... \right. \left|{\mu }_{K-1}>\right.]$$

(A2.1)

so that the projections of the vectors onto their corresponding states are as "close" as possible to the generating states, as shown in Fig.

Fig. 10

Quantum state, measurement vector and error vector

10 for a given state $\left|{\gamma }_{k}>\right.$, where the projections are given by the normalized inner products $<{\gamma }_{k}\left|{\mu }_{k}\right.>$ between the k-th measurement vector and its corresponding state, with the criterion of keeping the differences $\left|{e}_{k}\right.>=\left|{\gamma }_{k}\right.>-\left|{\mu }_{k}\right.>$ as small as possible; the SRM finds the measurement vectors minimizing the quadratic error as the sum of the square norm of the error vectors:

$$\mathcal{E}=\sum_{k=0}^{K-1}<{e}_{k}\left|{e}_{k}\right.>=\sum_{k=0}^{K-1}\left(<{\gamma }_{k}\left| -<{\mu }_{k}\left|)(\right.\right.\left|{\upgamma }_{k}\right.>- \left|{\upmu }_{k}\right.>\right)$$

(A2.2)

For the derivation of the optimal measurement matrix, the SRM method starts from the Gram matrix $\mathcal{G}$ of the constellation ${\varvec{\Gamma}}$; $\mathcal{G}$ is a Hermitian positive definite K × K square matrix, obtained from the inner products between all couples of composite states:

$$ {\mathbf{\mathcal{G}}} = {{\varvec{\Gamma}}}^{\user2{*}} {{\varvec{\Gamma}}},{\text{with elements}}:{\mathcal{G}}_{kl} = \left\langle {\gamma_{k} \left| {\gamma_{l} } \right.} \right\rangle ,k,l = 0,1, \ldots , K - 1 $$

(A2.3)

the optimal measurement matrix is given by [1]:

$$\boldsymbol{\mathcal{M}}={\varvec{\Gamma}}{\boldsymbol{\mathcal{G}}}^{-1/2}$$

(A2.4)

where the inverse square root matrix ${{\varvec{G}}}^{-1/2}$ has the elements ${G}_{kl}^{-1/2}$; the measurement vectors are then given by the linear combinations of the generating states:

$$\left|{\mu }_{k}>\right.=\sum_{l=0}^{K-1}{\mathcal{G}}_{kl}^{-1/2}\left|{\gamma }_{l}>\right.$$

(A2.5)

the measurement vectors are then used to form the rank-one POVMs [81, 82]:

$${\Pi }_{k}=\left|{\mu }_{k}>\right.<{\mu }_{k}|;\sum_{k}{\Pi }_{k}=1$$

(A2.6)