Skip to main content
SpringerLink
Log in

Quantum channel estimations via indefinite causal order

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

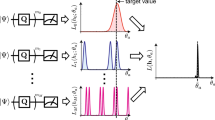
In this paper, we consider the quantum switch, which is one of the indefinite causal structures, in the study of quantum channel estimation. We show that such an indefinite causal order cannot provide any advantage for estimating quantum channels when the Kraus operators of the channel are commutative. We investigate the effects of the quantum switch when studying unitary qubit channels and amplitude damping qubit channels with noncommutative Kraus operators.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data Availability

This manuscript has no associated data

References

  1. Fujiwara, A.: Quantum channel identification problem. Phys. Rev. A 63(4), 042304 (2001)

    Article  ADS  Google Scholar 

  2. Fujiwara, A., Algoet, P.: One-to-one parametrization of quantum channels. Phys. Rev. A 59, 3290–3294 (1999)

    Article  ADS  Google Scholar 

  3. Helstrom, C.: Minimum mean-squared error of estimates in quantum statistics. Phys. Lett. A 25(2), 101–102 (1967)

    Article  ADS  Google Scholar 

  4. Holevo, A.S.: Probabilistic and Statistical Aspects of Quantum Theory. North-Holland, Amsterdam (1982)

    MATH  Google Scholar 

  5. Maccone, L., Cillis, G.D.: Robust strategies for lossy quantum interferometry. Phys. Rev. A 79(2), 023812 (2008)

    Article  ADS  Google Scholar 

  6. Chiribella, G., D’Ariano, G.M., Perinotti, P.: Memory effects in quantum channel discrimination. Phys. Rev. Lett. 101(18), 180501 (2008)

    Article  ADS  Google Scholar 

  7. Van, D.W., D’Ariano, G.M., Mauro, E.A., et al.: Optimal quantum circuits for general phase estimation. Phys. Rev. Lett. 98(9), 090501 (2007)

    Article  ADS  Google Scholar 

  8. Takeoka, M., Wilde, M.M.: Optimal estimation and discrimination of excess noise in thermal and amplifier channels (2016). arXiv:1611.09165

  9. Wu, X., Duan, R.: Exact quantum search by parallel unitary discrimination schemes. Phys. Rev. A 78(1), 012303 (2008)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  10. Duan, R., Guo, C., Li, C.K., Li, Y.: Parallel distinguishability of quantum operations. In: 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, pp. 2259–2263 (2016)

  11. Collins, D., Stephens, J.: Depolarizing-channel parameter estimation using noisy initial states. Phys. Rev. A 92(3), 032324 (2015)

    Article  ADS  Google Scholar 

  12. Liu, J., Yuan, H.: Quantum parameter estimation with optimal control. Phys. Rev. A 96(1), 012117 (2017)

    Article  ADS  Google Scholar 

  13. Oreshkov, O., Costa, F., Brukner, Č: Quantum correlations with no causal order. Nat. Commun. 3(10), 1092 (2012)

    Article  ADS  Google Scholar 

  14. Chiribella, G., D’Ariano, G.M., Perinotti, P., et al.: Quantum computations without definite causal structure. Phys. Rev. A 88(2), 022318 (2013)

    Article  ADS  Google Scholar 

  15. Araújo, M., Guérin, P.A., Baumeler, Ä.: Quantum computation with indefinite causal structures. Phys. Rev. A 96(5), 052315 (2017)

    Article  ADS  Google Scholar 

  16. Feix, A., Araújo, M., Brukner, Č: Quantum superposition of the order of parties as a communication resource. Phys. Rev. A 92(5), 052326 (2015)

    Article  ADS  Google Scholar 

  17. Araújo, M., Costa, F., Brukner, Č: Computational advantage from quantum-controlled ordering of gates. Phys. Rev. Lett. 113(25), 250402 (2014)

    Article  ADS  Google Scholar 

  18. Ebler, D., Salek, S., Chiribella, G.: Enhanced communication with the assistance of indefinite causal order. Phys. Rev. Lett. 120(12), 120502 (2018)

    Article  ADS  Google Scholar 

  19. Goswami, K., Costa, F.: Classical communication through quantum causal structures. Phys. Rev. A 103(4), 042606 (2021)

    Article  ADS  MathSciNet  Google Scholar 

  20. Chiribella, G., Banik, M., Bhattacharya, S.S., et al.: Indefinite causal order enables perfect quantum communication with zero capacity channel. New J. Phys. 23(3), 033039 (2021)

    Article  ADS  MathSciNet  Google Scholar 

  21. Chiribella, G.: Perfect discrimination of no-signalling channels via quantum superposition of causal structures. Phys. Rev. A 86(4), 040301 (2012)

    Article  ADS  MathSciNet  Google Scholar 

  22. Bavaresco, J., Murao, M., Quintino, M.T.: Strict hierarchy between parallel, sequential, and indefinite-causal-order strategies for channel discrimination. Phys. Rev. Lett. 127(20), 200504 (2021)

    Article  ADS  MathSciNet  Google Scholar 

  23. Bavaresco, J., Murao, M., Quintino, M.T.: Unitary channel discrimination beyond group structures: advantages of sequential and indefinite-causal-order strategies. J. Math. Phys. 63(4), 042203 (2022)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  24. Frey, M.: Indefinite causal order aids quantum depolarizing channel identification. Quant. Inf. Process. 18(4), 96–115 (2019)

    Article  ADS  MATH  Google Scholar 

  25. Zhao, X.B., Yang, Y.X., Chiribella, G.: Quantum metrology with indefinite causal order. Phys. Rev. Lett. 124(19), 190503 (2020)

    Article  ADS  MathSciNet  Google Scholar 

  26. Yin, P., Zhao, X.B., Yang, Y.X., et al.: Experimental super-Heisenberg quantum metrology with indefinite gate order. Nat. Phys. 8, 1–6 (2023)

    Google Scholar 

  27. Mukhopadhyay, C., Gupta, M.K., Pati, A.K.: Superposition of causal order as a metrological resource for quantum thermometry (2018). arXiv: 1812.07508

  28. Chapeau-Blondeau, F.: Noisy quantum metrology with the assistance of indefinite causal order. Phys. Rev. A 103(3), 032615 (2021)

    Article  ADS  MathSciNet  Google Scholar 

  29. Chapeau-Blondeau, F.: Indefinite causal order for quantum metrology with quantum thermal noise. Phys. Lett. A 447, 128300 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  30. Kurdzialek, S., Gorecki, W., Albarelli, F., Demkowicz-Dobrzanski, R.: Using adaptiveness and causal superpositions against noise in quantum metrology (2022). arXiv: 2212.08106

  31. Liu, Q.S., Hu, Z.H., Yuan, H., Yang, Y.X.: Optimal strategies of quantum metrology with a strict hierarchy. Phys. Rev. Lett. 130, 070803 (2023)

    Article  ADS  MathSciNet  Google Scholar 

  32. Lu, X.M., Wang, X., Sun, C.P.: Quantum Fisher information flow and non-Markovian processes of open systems. Phys. Rev. A 82(4), 042103 (2010)

    Article  ADS  Google Scholar 

  33. Fraïsse, J.M.E., Braun, D.: Quantum channel-estimation with particle loss: GHZ versus W states. Quant. Meas. Quant. Metrol. 3(1), 53–67 (2016)

    Google Scholar 

  34. Ji, Z., Wang, G., Duan, R., et al.: Parameter estimation of quantum channels. IEEE Trans. Inf. Theory 54(11), 5172–5185 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  35. Zhong, W., Sun, Z., Ma, J., et al.: Fisher information under decoherence in Bloch representation. Phys. Rev. A 87(2), 022337 (2013)

    Article  ADS  Google Scholar 

  36. Šafránek, D.: Simple expression for the quantum Fisher information matrix. Phys. Rev. A 97(4), 042322 (2018)

    Article  ADS  Google Scholar 

  37. Kraus, K.: States, Effects, and Operations: Fundamental Notions of Quantum Theory. Springer, Berlin (1983)

    Book  MATH  Google Scholar 

  38. Nielsen, M.A., Caves, C.M., Schumacher, B., Barnum, H.: Information-theoretic approach to quantum error correction and reversible measurement. Proc. R. Soc. A Math. Phys. Eng. Sci. 454(1969), 277–304 (1998)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  39. Suzuki, J.: Entanglement detection and parameter estimation of quantum channels. Phys. Rev. A 94(4), 042306 (2016)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

Z. Yin was partially supported by NSFC No. 12031004.

Author information

Authors and Affiliations

  1. School of Mathematics and Information Sciences, Yantai University, Yantai, 264005, China

    Juan Gu

  2. School of Mathematics and Statistics, Central South University, Changsha, 410083, China

    Zhi Yin

  3. School of Mathematics, Harbin Institute of Technology, Harbin, 150006, China

    Longsuo Li

Authors
  1. Juan Gu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhi Yin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Longsuo Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Juan Gu.

Ethics declarations

Conflict of interest

No conflict of interest exits in this manuscript

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A: Generators of Lie algebras su(2) and su(4)

The generators of Lie algebra su(2) are given by

$$\begin{aligned} \eta _{1}=\left( \begin{array}{cc} 0&{}\quad 1\\ 1&{}\quad 0\nonumber \\ \end{array}\right) , \quad \eta _{2}=\left( \begin{array}{cc} 1&{}\quad 0\\ 0&{}\quad 1\nonumber \\ \end{array} \right) , \quad \eta _{3}=\left( \begin{array}{cc} 0&{}\quad -i\\ i&{}\quad 0 \end{array} \right) . \end{aligned}$$

And the generators of Lie algebra su(4) are given by

$$\begin{aligned} \eta _{1}= & {} \left( \begin{array}{cccc} 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ \end{array} \right) , \quad \eta _{2}=\left( \begin{array}{cccc} 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ \end{array}\right) , \quad \eta _{3}=\left( \begin{array}{cccc} 0&{}\quad 0&{}\quad 0&{}\quad 1\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 1&{}\quad 0&{}\quad 0&{}\quad 0\\ \end{array}\right) ,\\ \eta _{4}= & {} \left( \begin{array}{cccc} 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ \end{array}\right) , \eta _{5}= \left( \begin{array}{cccc} 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0\\ \end{array} \right) , \quad \eta _{6}= \left( \begin{array}{cccc} 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1\\ 0&{}\quad 0&{}\quad 1&{}\quad 0\\ \end{array} \right) , \\ \eta _{7}= & {} \left( \begin{array}{cccc} 0&{}\quad -i&{}\quad 0&{}\quad 0\\ i&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ \end{array} \right) , \eta _{8}= \left( \begin{array}{cccc} 0&{}\quad 0&{}\quad -i&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ i&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ \end{array} \right) , \eta _{9}= \left( \begin{array}{cccc} 0&{}\quad 0&{}\quad 0&{}\quad -i\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ i&{}\quad 0&{}\quad 0&{}\quad 0\\ \end{array} \right) , \\ \eta _{10}= & {} \left( \begin{array}{cccc} 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad -i&{}\quad 0\\ 0&{}\quad i&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ \end{array} \right) , \eta _{11}= \left( \begin{array}{cccc} 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad -i\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad i&{}\quad 0&{}\quad 0\\ \end{array} \right) , \quad \eta _{12}= \left( \begin{array}{cccc} 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad -i\\ 0&{}\quad 0&{}\quad i&{}\quad 0\\ \end{array} \right) ,\\ \eta _{13}= & {} \left( \begin{array}{cccc} 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad -1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ \end{array} \right) , \quad \eta _{14}=\frac{1}{\sqrt{3}} \left( \begin{array}{cccc} 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad -2&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ \end{array} \right) , \\ \eta _{15}= & {} \frac{1}{\sqrt{6}} \left( \begin{array}{cccc} 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad -3\\ \end{array} \right) . \end{aligned}$$

Appendix B: Coefficients of \(\rho _\theta \) in (29)

Recall that

$$\begin{aligned} \rho _{\theta }= & {} \mathcal {S}(\mathcal {U}_{1\theta },\mathcal {U}_{2\theta })(\rho ;|c\rangle ) = \begin{pmatrix} pE&{}\sqrt{p(1-p)}G\\ \sqrt{p(1-p)}H&{}(1-p)M\\ \end{pmatrix},\\ E= & {} \frac{1}{4} \{ 2+2(2q-1)\cos 2\theta +\sqrt{q(1-q)}(2-2\cos 4\theta ) \} |0\rangle \langle 0|\\{} & {} + \frac{1}{4} \{ 4\sqrt{q(1-q)}\cos 2\theta -2i[(1-2q)\sin 2\theta +\sqrt{q(1-q)}\sin 4\theta ] \} |0\rangle \langle 1|\\{} & {} + \frac{1}{4} \{ 4\sqrt{q(1-q)}\cos 2\theta +2i[(1-2q) \sin 2\theta +\sqrt{q(1-q)}\sin 4\theta ] \} |1\rangle \langle 0|\\{} & {} + \frac{1}{4} \{ 2+2(1-2q)\cos 2\theta +\sqrt{q(1-q)}(2\cos 4\theta -2)\}|1\rangle \langle 1|,\\ G= & {} \frac{1}{4} \{[3q-1+2\cos 2\theta +(q-1)\cos 4\theta +\sqrt{q(1-q)}(1-\cos 4\theta )]\\{} & {} -i[(2q-2)\sin 2\theta +(1-q)\sin 4\theta +\sqrt{q(1-q)}(\sin 4\theta -2\sin 2\theta )]\}|0\rangle \langle 0|\\{} & {} +\frac{1}{4} \{[\sqrt{q(1-q)}(3+\cos 4\theta )+q(1-\cos 4\theta )]\\{} & {} -i[-q\sin 4\theta +2(1-q)\sin 2\theta +\sqrt{q(1-q)}(\sin 4\theta +2\sin 2\theta )]\}|0\rangle \langle 1|\nonumber \\{} & {} +\frac{1}{4} \{[(1-q)(\cos 4\theta -1)+\sqrt{q(1-q)}(3+\cos 4\theta )]\\{} & {} -i[2q\sin 2\theta -(1-q)\sin 4\theta -\sqrt{q(1-q)}(\sin 4\theta +2\sin 2\theta )]\}|1\rangle \langle 0|\\{} & {} +\frac{1}{4} \{[2\cos 2\theta +2-3q+(\sqrt{q(1-q)}-q)\cos 4\theta -\sqrt{q(1-q)}]\\{} & {} -i[(2q-2\sqrt{q(1-q)})\sin 2\theta +(\sqrt{q(1-q)}-q)\sin 4\theta ]\} |1\rangle \langle 1|,\\ H= & {} \frac{1}{4}\{[3q-1+2\cos 2\theta +(q-1)\cos 4\theta +\sqrt{q(1-q)}(1-\cos 4\theta )]\\{} & {} +i[(2q-2)\sin 2\theta +(1-q)\sin 4\theta +\sqrt{q(1-q)}(\sin 4\theta -2\sin 2\theta )]\}|0\rangle \langle 0|\\{} & {} +\frac{1}{4} \{[(1-q)(\cos 4\theta -1)+\sqrt{q(1-q)}(3+\cos 4\theta )]\\{} & {} +i[2q\sin 2\theta -(1-q)\sin 4\theta -\sqrt{q(1-q)}(\sin 4\theta +2\sin 2\theta )]\}|0\rangle \langle 1|\\{} & {} +\frac{1}{4}\{[q(1-\cos 4\theta )+\sqrt{q(1-q)}(3+\cos 4\theta )]\\{} & {} +i[2(1-q)\sin 2\theta +\sqrt{q(1-q)}(2\sin 2\theta +\sin 4\theta )-q\sin 4\theta ]\}|1\rangle \langle 0|\\{} & {} +\frac{1}{4} \{[2\cos 2\theta +2-3q-\sqrt{q(1-q)}+(\sqrt{q(1-q)}-q)\cos 4\theta ]\\{} & {} +i[(2q-2\sqrt{q(1-q)})\sin 2\theta +(\sqrt{q(1-q)}-q)\sin 4\theta ] \} |1\rangle \langle 1|,\\ M= & {} \frac{1}{4} \{2+2(2q-1)\cos 2\theta \} |0\rangle \langle 0|\\{} & {} +\frac{1}{4} \{[(2q-1)(1-\cos 4\theta )+4\sqrt{q(1-q)}\cos 2\theta ]-i[(1-2q)\sin 4\theta \\{} & {} +4\sqrt{q(1-q)}\sin 2\theta ]\}|0\rangle \langle 1|+\frac{1}{4} \{[(2q-1)(1-\cos 4\theta )+4\sqrt{q(1-q)}\cos 2\theta ]\\{} & {} +i[(1-2q)\sin 4\theta +4\sqrt{q(1-q)}\sin 2\theta ]\}|1\rangle \langle 0|\\{} & {} +\frac{1}{4} \{2+2(1-2q)\cos 2\theta \} |1\rangle \langle 1|. \end{aligned}$$

The generalized Bloch expression of \(\rho _\theta \) is given by

$$\begin{aligned} \rho _{\theta }=\frac{1}{4}1\hspace{-2.22214pt}{\textrm{l}}_{4}+\frac{1}{2} \sum _{i=1}^{15} \omega _i \eta _i, \end{aligned}$$

with coefficients

$$\begin{aligned} \omega _{1}&=2p\sqrt{q(1-q)}\cos 2\theta , \\ \omega _{2}&=\frac{\sqrt{p(1-p)}}{2}[3q-1+\sqrt{q(1-q)}+2\cos 2\theta +(q-1-\sqrt{q(1-q)})\cos 4\theta ],\\ \omega _{3}&=\frac{\sqrt{p(1-p)}}{2}[q+3\sqrt{q(1-q)}-(q-\sqrt{q(1-q)})\cos 4\theta ],\\ \omega _{4}&=\frac{\sqrt{p(1-p)}}{2}[q-1+3\sqrt{q(1-q)}+(1-q+\sqrt{q(1-q)})\cos 4\theta ],\\ \omega _{5}&=\frac{\sqrt{p(1-p)}}{2}[2-3q-\sqrt{q(1-q)}+2\cos 2\theta +(\sqrt{q(1-q)}-q)\cos 4\theta ],\\ \omega _{6}&=\frac{1-p}{2}[2q-1-(2q-1)\cos 4\theta +4\sqrt{q(1-q)}\cos 2\theta ],\\ \omega _{7}&=p[(1-2q)\sin 2\theta +\sqrt{q(1-q)}\sin 4\theta ],\\ \omega _{8}&=\frac{\sqrt{p(1-p)}}{2}[(2q-2-2\sqrt{q(1-q)})\sin 2\theta +(1-q+\sqrt{q(1-q)})\sin 4\theta ],\\ \omega _{9}&=\frac{\sqrt{p(1-p)}}{2}[(2-2q+2\sqrt{q(1-q)})\sin 2\theta +(\sqrt{q(1-q)}-q)\sin 4\theta ],\\ \omega _{10}&=\frac{\sqrt{p(1-p)}}{2}[(2q-2\sqrt{q(1-q)})\sin 2\theta -(1-q+\sqrt{q(1-q)})\sin 4\theta ],\\ \omega _{11}&=\frac{\sqrt{p(1-p)}}{2}[(2q-2\sqrt{q(1-q)})\sin 2\theta +(\sqrt{q(1-q)}-q)\sin 4\theta ],\\ \omega _{12}&=\frac{1-p}{2}[(1-2q)\sin 4\theta +4\sqrt{q(1-q)}\sin 2\theta ],\\ \omega _{13}&=p[(2q-1)\cos 2\theta +\sqrt{q(1-q)}(1-\cos 4\theta )],\\ \omega _{14}&=\frac{1}{\sqrt{3}}-\frac{1}{\sqrt{3}}(1-p)[2+(2q-1)\cos 2\theta ],\\ \omega _{15}&=\frac{1}{\sqrt{6}}-\frac{\sqrt{6}}{3}(1-p)[1+(1-2q)\cos 2\theta ]. \end{aligned}$$

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gu, J., Yin, Z. & Li, L. Quantum channel estimations via indefinite causal order. Quantum Inf Process 22, 369 (2023). https://doi.org/10.1007/s11128-023-04118-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-023-04118-7

Keywords

Search

Navigation