Quantum machine learning based on continuous variable single-photon states: an elementary foundation for quantum neural networks

Abstract

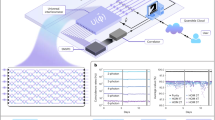
Photonic quantum computing is a leading approach toward universal quantum computation. Here, we propose a realistic model for the implementation of neural networks on photonic quantum computers. Specially, we design a quantum circuit built in the continuous-variable (CV) architecture that encodes information in the spectral amplitude functions of single-photons. This circuit consisting of some electro-optical modulators and XOR boxes that, respectively, adjust and combine their entries to provide a weighted sum of input signals. We show that our model can reproduce classical neural network models while maintaining some quantum phenomena such as superposition and entanglement. In particular, we utilize the circuit as a quantum classifier and validate the CV quantum neural network architecture through doing some machine learning modeling experiments. Such a quantum circuit can be implemented on the CV photonic quantum computers that promise exponential speed-up over the classical computers for specific tasks.

Supplementary

1.1 Single-photon states

A single-photon can be introduced via a superposition of different spectral components, to encode an N-level qudit, where N can generally be arbitrarily large. Performing such encoding requires a set of spectral functions $\{\Psi _i(\omega )\}$, where $\omega$ is the frequency relative to a central carrier frequency [12].

Since the photonic spectral degree of freedom is continuous, in principle infinite information could be encoded and transmitted by a single-photon state. However, the communicable information is reduced subject to realistic channel, detector, and photon engineering constraints. Ideally, orthonormal basis, $\int _{-\infty }^{+\infty } {\textrm{d}}\omega \Psi _i(\omega )\Psi _i^*(\omega )=\delta _{ij}$ would be of interest, since they can always be perfectly distinguished with an appropriate measurement device. Nevertheless, in reality, such orthogonality may only be achieved approximately. Figure 8 shows a specific Gaussian spectral basis with the same variance centered at different frequencies. Assuming the Gaussian distributions with zero variance, one could achieve orthonormality. However, this would be physically unrealistic. Photonic mode operators can be defined as ${\hat{A}}_{\Psi (\omega )}^\dagger = \int _{-\infty }^{+\infty } {\textrm{d}}\omega \Psi (\omega ){\hat{a}}^\dagger (\omega )$, which create photons with a well-defined spectral distribution function $\Psi (\omega )$, where ${\hat{a}}^\dagger$ is the single-frequency photonic creation operator in the spatial mode a [42]. A single-photonic state can be obtained as ${\hat{A}}_{\Psi (\omega )}^\dagger |0\rangle$ where $|0\rangle$ is the vacuum state. Accordingly, a spectral basis state may be expressed as $\rho (\omega )={\hat{A}}_{\Psi (\omega )}^\dagger |0\rangle \langle 0| {\hat{A}}_{\Psi (\omega )}$.

In principle, there are various basis $\{\Psi _i(\omega )\}$ such as frequency or temporal delta functions, wavelet families, Hermite polynomials, or any other set of functions satisfying orthonormality [12]. However, not all states can be readily engineered for quantum information and quantum computation [43,44,45].

Fig. 8

A particular encoding basis $\{\Psi _i(\omega )\}$, where the basis states are not perfectly orthogonal. Indeed, this is a Gaussian spectral basis with the same variance centered at different frequencies used to encode the input signals of a CV neural network

1.2 A quantum neuron with three input signals

For the sake of simplicity, we consider a simple circuit with three input signals as shown in Fig. 9. The initial state vector of the circuit reads as,

$$\begin{aligned} |\Psi ({\omega }_1,{\omega }_2,{\omega }_3)\rangle= & {} |1,\phi _1(\omega _1)\rangle \otimes |1,\phi _2(\omega _2)\rangle \otimes |1,\phi _3(\omega _3)\rangle \\= & {} \int {\textrm{d}}\omega _1 \phi _1(\omega _1) {\hat{a}}^\dagger (\omega _1)|0\rangle _1 \nonumber \\{} & {} \otimes \int {\textrm{d}}\omega _2 \phi _2(\omega _2) {\hat{a}}^\dagger (\omega _2)|0\rangle _2 \otimes \int {\textrm{d}}\omega _3 \phi _3(\omega _3) {\hat{a}}^\dagger (\omega _3)|0\rangle _3.\nonumber \end{aligned}$$

(14)

where,

$$\begin{aligned} \phi _i(\omega _i)= & {} \frac{1}{\big (2\pi \sigma _i^2\big )^{1/4}}e^{-\frac{\big (\omega _i-{\bar{\omega }}_i\big )^2}{4\sigma _i^2}}, \qquad i=1,2,3. \end{aligned}$$

(15)

At first, the signals enter the modulators that shift their central frequencies. The action of the modulator on the central frequency of each single-photon may be obtained as,

$$\begin{aligned} M(\eta _i)\phi _i(\omega _i)= & {} \frac{1}{(2\pi \sigma _i^2)^{1/4}}e^{-\frac{\big (\omega _i-\eta _i{\bar{\omega }}_i\big )^2}{4\sigma _i^2}}, \end{aligned}$$

(16)

where $\eta _i \in {\mathbb {R}}$ is a parameter that must be controlled (and updated) during the training process of the neural network. Now, we wish to establish a superposition of photonic states. Another useful unitary gate on a CV quantum computer is the XOR gate [46]. Each XOR concatenates its input signals, i.e., the two frequency-shifted single-photon states. Thus, the spectral amplitude function corresponding to the output of the first XOR can be written as,

$$\begin{aligned} \phi _{1,2}(\omega _1,\omega _2)= & {} \text {XOR}[\phi _{1}(\omega _1)\phi _{2}(\omega _2)]\\= & {} \frac{1}{\big (2\pi \sigma _1^2\big )^{1/4}}e^{-\frac{\omega _1^2}{4\sigma _1^2}} \times \frac{1}{\big (2\pi \sigma _2^2\big )^{1/4}}e^{-\frac{\big (\omega _2-\omega _1 -\eta _1{\bar{\omega }}_1-\eta _2{\bar{\omega }}_2\big )^2}{4\sigma _2^2}},\nonumber \end{aligned}$$

(17)

which implies that the spectral amplitudes of the output signals are entangled after passing through the XOR gate. In other words, the two single-photon states become entangled by the action of the XOR gate. Entanglement is a quantum phenomenon that has no classical counterpart and plays a key role in quantum computation.

Fig. 9

A circuit consisting of a series of Modulators $M(\eta )$ and XOR elements

Next, we consider the third qumode and try to find the output of the second XOR gate. Again, the XOR concatenates its photonic qumodes, therefore, the corresponding output qumode can be introduced by the following spectral amplitude function,

$$\begin{aligned} \phi _{1,2,3}(\omega _1,\omega _2,\omega _3)= & {} \frac{1}{\big (2\pi \sigma _1^2\big )^{1/4}}e^{-\frac{\omega _1^2}{4\sigma _1^2}} \times \frac{1}{\big (2\pi \sigma _2^2\big )^{1/4}}e^{-\frac{\big (\omega _2-\omega _1\big )^2}{4\sigma _2^2}} \\{} & {} \times \frac{1}{\big (2\pi \sigma _3^2\big )^{1/4}}e^{-\frac{\big (\omega _3 -\omega _2-\omega _1-\eta _1{\bar{\omega }}_1-\eta _2{\bar{\omega }}_2-\eta _3{\bar{\omega }}_3\big )^2}{4\sigma _3^2}}.\nonumber \end{aligned}$$

(18)

Therefore, the output state of the circuit can be obtained as,

$$\begin{aligned} |{\widetilde{\Psi }}({\omega }_1,{\omega }_2,{\omega }_2)\rangle= & {} XOR(N=3) M(\mathbf{\eta })|\Psi ({\omega }_1,{\omega }_2,{\omega }_2)\rangle \\= & {} \int {\textrm{d}}\omega _1 \int {\textrm{d}}\omega _2 \int {\textrm{d}}\omega _3 \phi _{123} (\omega _1,\omega _2,\omega _3) {\hat{a}}^\dagger (\omega _1)|0\rangle _1\nonumber \\{} & {} \otimes {\hat{a}}^\dagger (\omega _2)|0\rangle _2 \otimes {\hat{a}}^\dagger (\omega _3)|0\rangle _3.\nonumber \end{aligned}$$

(19)

where $M({\varvec{\eta }})$ denotes the modulators. This is an entangled state vector because the respective spectral amplitude function cannot be separated as below,

$$\begin{aligned} \phi _{123}(\omega _1,\omega _2,\omega _3) = \phi _1(\omega _1)\phi _2(\omega _2)\phi _3(\omega _3) \end{aligned}$$

(20)

From Eq. (19), one can obtain the density operator of the output of the circuit as,

$$\begin{aligned} \rho _{123}= & {} |{\widetilde{\Psi }}({\omega }_1,{\omega }_2,{\omega }_2)\rangle \langle {\widetilde{\Psi }}({\omega }_1,{\omega }_2,{\omega }_2)| \\= & {} \int {\textrm{d}}\omega _1 \int {\textrm{d}}\omega _2 \int {\textrm{d}}\omega _3 \int {\textrm{d}}\omega '_1 \int {\textrm{d}}\omega '_2 \int {\textrm{d}}\omega '_3 \phi _{123}(\omega _1,\omega _2,\omega _3) \phi _{123}(\omega '_1,\omega '_2,\omega '_3) \nonumber \\{} & {} \times {\hat{a}}^\dagger (\omega _1)|0\rangle _1 \langle 0|_1{\hat{a}} (\omega '_1) \otimes {\hat{a}}^\dagger (\omega _2)|0\rangle _2 \langle 0|_2 {\hat{a}} (\omega '_2) \otimes {\hat{a}}^\dagger (\omega _3)|0\rangle _3 \langle 0|_3 {\hat{a}} (\omega '_3).\nonumber \end{aligned}$$

(21)

Using Eq. (18), the density operator can be rewritten as,

$$\begin{aligned} \rho _{123}= & {} \frac{1}{\big (2\pi \sigma _1^2\big )^{1/2}} \frac{1}{\big (2\pi \sigma _2^2\big )^{1/2}} \frac{1}{\big (2\pi \sigma _3^2\big )^{1/2}}\int {\textrm{d}}\omega _1 \int {\textrm{d}}\omega _2 \int {\textrm{d}}\omega _3 \int {\textrm{d}}\omega '_1 \int {\textrm{d}}\omega '_2 \int {\textrm{d}}\omega '_3 \nonumber \\{} & {} \times e^{-\frac{\omega _1^2}{4\sigma _1^2}} e^{-\frac{{\omega '_1}^2}{4\sigma _1^2}} e^{-\frac{(\omega _2-\omega _1)^2}{4\sigma _2^2}} \nonumber \\{} & {} e^{-\frac{\big (\omega '_2-\omega '_1\big )^2}{4\sigma _2^2}} e^{-\frac{\big (\omega _3-\omega _2-\omega _1-\sum _{i=1}^{3} \eta _i {\bar{\omega }}_i\big )^2}{4\sigma _3^2}} e^{-\frac{\big (\omega '_3-\omega '_2-\omega '_1-\sum _{i=1}^{3} \eta _i {\bar{\omega }}_i\big )^2}{4\sigma _3^2}}\nonumber \\{} & {} \times {\hat{a}}^\dagger (\omega _1)|0\rangle _1 \langle 0|_1{\hat{a}} (\omega '_1) \otimes {\hat{a}}^\dagger (\omega _2)|0\rangle _2 \langle 0|_2 {\hat{a}} (\omega '_2) \otimes {\hat{a}}^\dagger (\omega _3)|0\rangle _3 \langle 0|_3 {\hat{a}} (\omega '_3).\nonumber \\ \end{aligned}$$

(22)

Now, we want to focus on the last qumode of the output state of the circuit, hence, we proceed to remove the other unwanted qumodes. To do this, we trace out the first and second qumodes as below,

$$\begin{aligned} \rho _{3}= & {} \textrm{Tr}_{1,2}(\rho _{123})= \int {\textrm{d}}\omega ''_1 \int {\textrm{d}}\omega ''_2 \langle 0|_1{\hat{a}} (\omega ''_1) \otimes \langle 0|_2{\hat{a}} (\omega ''_2) \rho _{123} {\hat{a}}^\dagger (\omega ''_1) |0\rangle _1 \otimes {\hat{a}}^\dagger (\omega ''_2) |0\rangle _2 \nonumber \\= & {} \frac{1}{\big (2\pi \sigma _1^2\big )^{1/2}} \frac{1}{\big (2\pi \sigma _2^2\big )^{1/2}} \frac{1}{\big (2\pi \sigma _3^2\big )^{1/2}}\int {\textrm{d}}\omega _1 \int {\textrm{d}}\omega _2 \int {\textrm{d}}\omega _3 \nonumber \\{} & {} \int {\textrm{d}}\omega '_1 \int {\textrm{d}}\omega '_2 \int {\textrm{d}}\omega '_3 \int {\textrm{d}}\omega ''_1 \int {\textrm{d}}\omega ''_2 \times e^{-\frac{\omega _1^2}{4\sigma _1^2}} e^{-\frac{{\omega '_1}^2}{4\sigma _1^2}} e^{-\frac{\big (\omega _2-\omega _1\big )^2}{4\sigma _2^2}}\nonumber \\{} & {} e^{-\frac{\big (\omega '_2-\omega '_1\big )^2}{4\sigma _2^2}} e^{-\frac{\big (\omega _3-\omega _2-\omega _1-\sum _{i=1}^{3} \eta _i {\bar{\omega }}_i\big )^2}{4\sigma _3^2}} e^{-\frac{\big (\omega '_3-\omega '_2-\omega '_1-\sum _{i=1}^{3} \eta _i {\bar{\omega }}_i\big )^2}{4\sigma _3^2}} \nonumber \\{} & {} \times \langle 0|_1{\hat{a}} (\omega ''_1) \otimes \langle 0|_2{\hat{a}} (\omega ''_2) \bigg [ {\hat{a}}^\dagger (\omega _1)|0\rangle _1 \langle 0|_1{\hat{a}} (\omega '_1) \nonumber \\{} & {} \otimes {\hat{a}}^\dagger (\omega _2)|0\rangle _2 \langle 0|_2 {\hat{a}} (\omega '_2) \otimes {\hat{a}}^\dagger (\omega _3)|0\rangle _3 \langle 0|_3 {\hat{a}} (\omega '_3) \bigg ] {\hat{a}}^\dagger (\omega ''_1) |0\rangle _1 \otimes {\hat{a}}^\dagger (\omega ''_2) |0\rangle _2,\nonumber \\ \end{aligned}$$

(23)

which can be simplified as,

$$\begin{aligned} \rho _{3}= & {} \frac{1}{(2\pi \sigma _1^2)^{1/2}} \frac{1}{\big (2\pi \sigma _2^2\big )^{1/2}} \frac{1}{\big (2\pi \sigma _3^2\big )^{1/2}}\int {\textrm{d}}\omega _1 \int {\textrm{d}}\omega _2 \int {\textrm{d}}\omega _3 \int {\textrm{d}}\omega '_3\\{} & {} \times e^{-\frac{\omega _1^2}{2\sigma _1^2}} e^{-\frac{\big (\omega _2-\omega _1\big )^2}{2\sigma _2^2}} e^{-\frac{\big (\omega _3-\omega _2-\omega _1-\sum _{i=1}^{3} \eta _i {\bar{\omega }}_i\big )^2}{4\sigma _3^2}} e^{-\frac{\big (\omega '_3-\omega _2-\omega _1-\sum _{i=1}^{3} \eta _i {\bar{\omega }}_i\big )^2}{4\sigma _3^2}} \nonumber \\{} & {} \times {\hat{a}}^\dagger (\omega _3) |0\rangle _3 \langle 0|_3 {\hat{a}} (\omega '_3),\nonumber \end{aligned}$$

(24)

where we have used the relation $\langle 0|_i {\hat{a}} (\omega '_i) {\hat{a}}^\dagger (\omega _j) |0\rangle _j=\langle {1_i\Vert 1_j}\rangle =\delta _{i,j}$ for $i,j=1,2$. Note that $|1_i\rangle$ denotes the state of a single-photon in the i-th mode. The states of two single-photons corresponding to different modes are orthogonal, i.e., $\langle {1_k\Vert 1_l}\rangle =\delta _{k,l}$ ($k \ne l$), while for the same modes we have $\langle {1_k\Vert 1_k}\rangle =1$ ($k,l=1,2,3$).

Now, let us check the normalization of the density operator of the output signal as below,

$$\begin{aligned} {{\textrm{Tr}}}(\rho _{3})= & {} \int {\textrm{d}}\omega ''_3 \langle 0| {\hat{a}} (\omega ''_3)\Vert \rho _{3}\Vert {\hat{a}}^\dagger (\omega ''_3)|0\rangle \\= & {} \frac{1}{\big (2\pi \sigma _1^2\big )^{1/2}} \frac{1}{\big (2\pi \sigma _2^2\big )^{1/2}} \frac{1}{\big (2\pi \sigma _3^2\big )^{1/2}}\int {\textrm{d}}\omega _1 \int {\textrm{d}}\omega _2 \int {\textrm{d}}\omega _3 \int {\textrm{d}}\omega '_3 \nonumber \\{} & {} \times e^{-\frac{\omega _1^2}{2\sigma _1^2}} e^{-\frac{\big (\omega _2-\omega _1\big )^2}{2\sigma _2^2}} e^{-\frac{\big (\omega _3-\omega _2-\omega _1-\sum _{i=1}^{3} \eta _i {\bar{\omega }}_i\big )^2}{4\sigma _3^2}} e^{-\frac{\big (\omega '_3-\omega _2-\omega _1-\sum _{i=1}^{3} \eta _i {\bar{\omega }}_i\big )^2}{4\sigma _3^2}} \nonumber \\{} & {} \times \langle 0| {\hat{a}} (\omega ''_3){\hat{a}}^\dagger (\omega _3) |0\rangle _3 \langle 0|_3 {\hat{a}} (\omega '_3){\hat{a}}^\dagger (\omega ''_3)|0\rangle ,\nonumber \end{aligned}$$

(25)

which can be simplified as,

$$\begin{aligned} {{{\textrm{Tr}}}}(\rho _{3})= & {} \frac{1}{(2\pi \sigma _1^2)^{1/2}} \frac{1}{\big (2\pi \sigma _2^2\big )^{1/2}} \frac{1}{\big (2\pi \sigma _3^2\big )^{1/2}}\int {\textrm{d}}\omega _1 \int {\textrm{d}}\omega _2 \int {\textrm{d}}\omega _3 \\{} & {} \times e^{-\frac{\omega _1^2}{2\sigma _1^2}} e^{-\frac{\big (\omega _2-\omega _1\big )^2}{2\sigma _2^2}} e^{-\frac{\big (\omega _3-\omega _2-\omega _1-\sum _{i=1}^{3} \eta _i {\bar{\omega }}_i\big )^2}{2\sigma _3^2}},\nonumber \end{aligned}$$

(26)

by computing the Gaussian integrals, one can readily show that ${{\textrm{Tr}}}(\rho _{3})=1$.

It is worth to note that the bias can be added by considering an additional photonic state, i.e., the zero-th qumode with $b=\eta _0$ and a Gaussian distribution centered at ${\bar{\omega }}_0=1$. Therefore, we can replace $\sum _{i=1}^{3} \eta _i {\bar{\omega }}_i$ by $b+\sum _{i=1}^{3} \eta _i {\bar{\omega }}_i=\sum _{i=0}^{3} \eta _i {\bar{\omega }}_i$ in Eq. (25).

The diagonal elements of the density operator, which can be obtained via the ideal homodyne measurement, provide the probabilities of reading the frequency $\omega$ of the third qumode,

$$\begin{aligned} P(\omega )&:= \langle 0| {\hat{a}} (\omega )\Vert \rho _{3}\Vert {\hat{a}}^\dagger (\omega )|0\rangle \\&= \frac{1}{\big (2\pi \sigma _1^2\big )^{1/2}} \frac{1}{\big (2\pi \sigma _2^2\big )^{1/2}} \frac{1}{(2\pi \sigma _3^2)^{1/2}} \int {\textrm{d}}\omega _1 \int {\textrm{d}}\omega _2 \int {\textrm{d}}\omega _3 \int {\textrm{d}}\omega '_3 \nonumber \\&\quad \times e^{-\frac{\omega _1^2}{2\sigma _1^2}} e^{-\frac{\big (\omega _2-\omega _1\big )^2}{2\sigma _2^2}} e^{-\frac{\big (\omega _3-\sum _{i=0}^{3} \eta _i {\bar{\omega }}_i\big )^2}{4\Delta ^2}} \nonumber \\&\quad e^{-\frac{\big (\omega '_3-\sum _{i=0}^{3} \eta _i {\bar{\omega }}_i\big )^2}{4\Delta ^2}} \langle 0| {\hat{a}} (\omega ){\hat{a}}^\dagger (\omega _3) |0\rangle _3 \langle 0|_3 {\hat{a}} (\omega '_3){\hat{a}}^\dagger (\omega )|0\rangle ,\nonumber \end{aligned}$$

(27)

which can be simplified as,

$$\begin{aligned} P(\omega )= & {} \frac{1}{\sqrt{2\pi \Delta ^2}} \exp \left[ {-\frac{\big (\omega -\sum _{i=0}^{3} \eta _i {\bar{\omega }}_i\big )^2}{2\Delta ^2}}\right] \end{aligned}$$

(28)

where $\Delta ^2= 4\sigma _1^2+\sigma _2^2+\sigma _3^2$. The above relation is a normal Gaussian distribution which implies that,

$$\begin{aligned} \int {\textrm{d}}\omega P(\omega )=1. \end{aligned}$$

(29)

Now, we know the probability distribution of the outcome of the circuit which can be used for quantum machine learning. The most probable outcome of the circuit can be obtained as,

$$\begin{aligned} \omega _m=\sum _{i=0}^{3} \eta _i {\bar{\omega }}_i. \end{aligned}$$

(30)

Consequently, a sequence of Gaussian gates, i.e., modulators and XORs followed by homodyne measurement as a non-Gaussian operation, lead to the desired transformation $|1,\phi (\omega _1)\rangle \otimes |1,\phi (\omega _2)\rangle \otimes |1,\phi (\omega _3)\rangle \rightarrow P(\omega ) \rightarrow \omega _m$. This transformation recalls a single-layer classical neural network. Note that the outcome of the circuit can be used in different ways based on the defined goals. Here, we use the most probable outcome of the circuit for the binary classification tasks. As mentioned, Eq. (28) is a normal Gaussian distribution which implies that one can use this for other classification tasks dealing with Gaussian samples.