Skip to main content

Advertisement

Springer Nature Link
Log in

Dynamical Casimir effect in a hybrid cavity optomechanical system

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

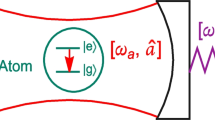
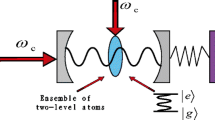
In this paper, we show that the dynamical Casimir effect can be observed in a hybrid cavity optomechanical system. By introducing a two-level atom into the cavity, the atomic transition from an excited state to the ground state can evoke a two-photon process. Our proposal does not require a driving field to induce the dynamical Casimir effect, which is very alternative to previous schemes. Furthermore, we show that when the atom is replaced by an identical atomic ensemble, the system not only can simulate the similar dynamic Casimir effect, but also exist more plentiful physical phenomena, i.e., higher-order resonance. Numerical simulation confirms the validity of our derivation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Schwinger, J.: On gauge invariance and vacuum polarization. Phys. Rev. 82, 664–679 (1951). https://doi.org/10.1103/PhysRev.82.664

    Article  ADS  MathSciNet  Google Scholar 

  2. Unruh, W.G.: Notes on black-hole evaporation. Phys. Rev. D 14, 870–892 (1976). https://doi.org/10.1103/PhysRevD.14.870

    Article  ADS  Google Scholar 

  3. Settineri, A., Macrì, V., Garziano, L., Di Stefano, O., Nori, F., Savasta, S.: Conversion of mechanical noise into correlated photon pairs: dynamical Casimir effect from an incoherent mechanical drive. Phys. Rev. A 100, 022501 (2019). https://doi.org/10.1103/PhysRevA.100.022501

    Article  ADS  Google Scholar 

  4. Del Grosso, N.F., Lombardo, F.C., Villar, P.I.: Photon generation via the dynamical Casimir effect in an optomechanical cavity as a closed quantum system. Phys. Rev. A 100, 062516 (2019). https://doi.org/10.1103/PhysRevA.100.062516

    Article  ADS  MathSciNet  Google Scholar 

  5. Agustí, A., Solano, E., Sabín, C.: Entanglement through qubit motion and the dynamical Casimir effect. Phys. Rev. A 99, 052328 (2019). https://doi.org/10.1103/PhysRevA.99.052328

    Article  ADS  Google Scholar 

  6. Ferreri, A., Bruschi, D.E., Wilhelm, F.K., Nori, F., Macrì, V.: Phonon-photon conversion as mechanism for cooling and coherence transfer (2023) arXiv:2312.09837

  7. Kadijani, S.S., Grosso, N.D., Schmidt, T.L., Farias, M.B.: Dynamical Casimir cooling in circuit QED systems (2023) arXiv:2312.09893

  8. Sorge, F.: Gravitational memory of Casimir effect. Phys. Rev. D 108, 104003 (2023). https://doi.org/10.1103/PhysRevD.108.104003

    Article  ADS  MathSciNet  Google Scholar 

  9. Gorban, M.J., Julius, W.D., Radhakrishnan, R., Cleaver, G.B.: Interference phenomena in the asymmetric dynamical Casimir effect for a single \(\delta -{\delta }{^{\prime }}\) mirror. Phys. Rev. D 108, 096037 (2023). https://doi.org/10.1103/PhysRevD.108.096037

    Article  ADS  MathSciNet  Google Scholar 

  10. Nakata, K., Suzuki, K.: Magnonic Casimir effect in ferrimagnets. Phys. Rev. Lett. 130, 096702 (2023). https://doi.org/10.1103/PhysRevLett.130.096702

    Article  ADS  Google Scholar 

  11. Wilson, C.M., Johansson, G., Pourkabirian, A., Simoen, M., Johansson, J.R., Duty, T., Nori, F., Delsing, P.: Observation of the dynamical Casimir effect in a superconducting circuit. Nature 479(7373), 376–379 (2011). https://doi.org/10.1038/nature10561

    Article  ADS  Google Scholar 

  12. Dalvit, D.A.: Shaking photons out of the vacuum. Nature 479(7373), 303–304 (2011). https://doi.org/10.1038/479303a

    Article  ADS  Google Scholar 

  13. Lähteenmäki, P., Paraoanu, G., Hassel, J., Hakonen, P.J.: Dynamical Casimir effect in a Josephson metamaterial. Proc. Natl. Acad. Sci. USA 110(11), 4234–4238 (2013). https://doi.org/10.1073/pnas.1212705110

    Article  ADS  Google Scholar 

  14. Ning, W., Huang, X.-J., Han, P.-R., Li, H., Deng, H., Yang, Z.-B., Zhong, Z.-R., Xia, Y., Xu, K., Zheng, D., Zheng, S.-B.: Deterministic entanglement swapping in a superconducting circuit. Phys. Rev. Lett. 123, 060502 (2019). https://doi.org/10.1103/PhysRevLett.123.060502

    Article  ADS  Google Scholar 

  15. Xu, Z., Gao, X., Bang, J., Jacob, Z., Li, T.: Non-reciprocal energy transfer through the Casimir effect. Nat. Nanotechnol. 17, 148 (2021). https://doi.org/10.1038/s41565-021-01026-8

    Article  ADS  Google Scholar 

  16. Xu, Z., Ju, P., Gao, X., Shen, K., Jacob, Z., Li, T.: Observation and control of Casimir effects in a sphere-plate-sphere system. Nat. Commun. 13, 6148 (2022). https://doi.org/10.1038/s41467-022-33915-4

    Article  ADS  Google Scholar 

  17. Kienzler, D., Flühmann, C., Negnevitsky, V., Lo, H.-Y., Marinelli, M., Nadlinger, D., Home, J.P.: Observation of quantum interference between separated mechanical oscillator wave packets. Phys. Rev. Lett. 116, 140402 (2016). https://doi.org/10.1103/PhysRevLett.116.140402

    Article  ADS  Google Scholar 

  18. Safavi-Naeini, A.H., Alegre, T.M., Chan, J., Eichenfield, M., Winger, M., Lin, Q., Hill, J.T., Chang, D.E., Painter, O.: Electromagnetically induced transparency and slow light with optomechanics. Nature 472(7341), 69–73 (2011). https://doi.org/10.1038/nature09933

    Article  ADS  Google Scholar 

  19. Zhong, Z.-R., Chen, L., Sheng, J.-Q., Shen, L.-T., Zheng, S.-B.: Multiphonon-resonance quantum Rabi model and adiabatic passage in a cavity-optomechanical system. Front. Phys. 17, 1–9 (2022). https://doi.org/10.1007/s11467-021-1092-7

    Article  Google Scholar 

  20. Chen, L., An, X.-W., Deng, T.-H., Zhong, Z.-R.: Toward multimode quantum Rabi model in a strong-coupling cavity optomechanical system. Quantum Inf. Process. 21(7), 232 (2022). https://doi.org/10.1007/s11128-022-03575-w

    Article  ADS  MathSciNet  Google Scholar 

  21. Macrì, V., Ridolfo, A., Di Stefano, O., Kockum, A.F., Nori, F., Savasta, S.: Nonperturbative dynamical Casimir effect in optomechanical systems: vacuum Casimir-Rabi splittings. Phys. Rev. X 8, 011031 (2018). https://doi.org/10.1103/PhysRevX.8.011031

    Article  Google Scholar 

  22. Qin, W., Macrì, V., Miranowicz, A., Savasta, S., Nori, F.: Emission of photon pairs by mechanical stimulation of the squeezed vacuum. Phys. Rev. A 100, 062501 (2019). https://doi.org/10.1103/PhysRevA.100.062501

    Article  ADS  Google Scholar 

  23. Long, X., He, W.-T., Zhang, N.-N., Tang, K., Lin, Z., Liu, H., Nie, X., Feng, G., Li, J., Xin, T., Ai, Q., Lu, D.: Entanglement-enhanced quantum metrology in colored noise by quantum zeno effect. Phys. Rev. Lett. 129, 070502 (2022). https://doi.org/10.1103/PhysRevLett.129.070502

    Article  ADS  Google Scholar 

  24. He, W.-T., Guang, H.-Y., Li, Z.-Y., Deng, R.-Q., Zhang, N.-N., Zhao, J.-X., Deng, F.-G., Ai, Q.: Quantum metrology with one auxiliary particle in a correlated bath and its quantum simulation. Phys. Rev. A 104, 062429 (2021). https://doi.org/10.1103/PhysRevA.104.062429

    Article  ADS  MathSciNet  Google Scholar 

  25. e Souza, R.M., Impens, F., Neto, P.A.M.: Microscopic dynamical Casimir effect. Phys. Rev. A 97, 032514 (2018). https://doi.org/10.1103/PhysRevA.97.032514

    Article  ADS  Google Scholar 

  26. Ferreri, A., Domina, M., Rizzuto, L., Passante, R.: Spontaneous emission of an atom near an oscillating mirror. Symmetry 11(11), 1384 (2019). https://doi.org/10.3390/sym11111384

    Article  ADS  Google Scholar 

  27. Dolan, B.P., Hunter-McCabe, A., Twamley, J.: Shaking photons from the vacuum: acceleration radiation from vibrating atoms. New J. Phys. 22(3), 033026 (2020). https://doi.org/10.1088/1367-2630/ab7bd5

    Article  ADS  MathSciNet  Google Scholar 

  28. Motazedifard, A., Dalafi, A., Naderi, M., Roknizadeh, R.: Controllable generation of photons and phonons in a coupled Bose-Einstein condensate-optomechanical cavity via the parametric dynamical Casimir effect. Ann. Phys. (N.Y.) 396, 202–219 (2018). https://doi.org/10.1016/j.aop.2018.07.013

    Article  ADS  Google Scholar 

  29. Lo, L., Law, C.K.: Quantum radiation from a shaken two-level atom in vacuum. Phys. Rev. A 98, 063807 (2018). https://doi.org/10.1103/PhysRevA.98.063807

    Article  ADS  Google Scholar 

  30. Wang, Y.P., Zhang, Z.C., Yu, Y.F., Zhang, Z.M.: Effects of the Casimir force on the properties of a hybrid optomechanical system. Chin. Phys. B 28, 1 (2019). https://doi.org/10.1088/1674-1056/28/1/014202

    Article  Google Scholar 

  31. Pirkkalainen, J.M., Cho, S.U., Massel, F., Tuorila, J., Heikkilä, T.T., Hakonen, P.J., Sillanpää, M.A.: Cavity optomechanics mediated by a quantum two-level system. Nat. Commun. 6(1), 6981 (2015). https://doi.org/10.1038/ncomms7981

    Article  ADS  Google Scholar 

  32. Zhong, Z.-R., Wang, X., Qin, W.: Towards quantum entanglement of micromirrors via a two-level atom and radiation pressure. Front. Phys. 13, 1–11 (2018). https://doi.org/10.1007/s11467-018-0824-9

    Article  Google Scholar 

  33. Neumeier, L., Northup, T.E., Chang, D.E.: Reaching the optomechanical strong-coupling regime with a single atom in a cavity. Phys. Rev. A 97, 063857 (2018). https://doi.org/10.1103/PhysRevA.97.063857

    Article  ADS  Google Scholar 

  34. Chen, B., Shang, L., Wang, X.-F., Chen, J.-B., Xue, H.-B., Liu, X., Zhang, J.: Atom-assisted second-order sideband generation in an optomechanical system with atom-cavity-resonator coupling. Phys. Rev. A 99, 063810 (2019). https://doi.org/10.1103/PhysRevA.99.063810

    Article  ADS  Google Scholar 

  35. Han, Y., Xue, L., Zhang, J.: Superradiance and collective gain in the atom-assisted multimode optomechanical system. Int. J. Theor. Phys. 58, 992–1000 (2019). https://doi.org/10.1007/s10773-018-3990-1

    Article  Google Scholar 

  36. Wu, E., Li, D., Li, F., Ma, Y.: Enhanced entanglement between two mechanical resonators in two optomechanical cavities with an atomic medium. Int. J. Theor. Phys. 56, 1665–1672 (2017). https://doi.org/10.1007/s10773-017-3307-9

    Article  Google Scholar 

  37. Lo, L., Fong, P.T., Law, C.K.: Dynamical Casimir effect in resonance fluorescence. Phys. Rev. A 102, 033703 (2020). https://doi.org/10.1103/PhysRevA.102.033703

    Article  ADS  Google Scholar 

  38. Joshi, A.: Nonlinear dynamical evolution of the driven two-photon Jaynes-cummings model. Phys. Rev. A 62, 043812 (2000). https://doi.org/10.1103/PhysRevA.62.043812

    Article  ADS  Google Scholar 

  39. Felicetti, S., Pedernales, J.S., Egusquiza, I.L., Romero, G., Lamata, L., Braak, D., Solano, E.: Spectral collapse via two-phonon interactions in trapped ions. Phys. Rev. A 92, 033817 (2015). https://doi.org/10.1103/PhysRevA.92.033817

    Article  ADS  Google Scholar 

  40. Garbe, L., Egusquiza, I.L., Solano, E., Ciuti, C., Coudreau, T., Milman, P., Felicetti, S.: Superradiant phase transition in the ultrastrong-coupling regime of the two-photon Dicke model. Phys. Rev. A 95, 053854 (2017). https://doi.org/10.1103/PhysRevA.95.053854

    Article  ADS  Google Scholar 

  41. Law, C.K.: Interaction between a moving mirror and radiation pressure: A Hamiltonian formulation. Phys. Rev. A 51, 2537–2541 (1995). https://doi.org/10.1103/PhysRevA.51.2537

    Article  ADS  Google Scholar 

  42. Aspelmeyer, M., Kippenberg, T.J., Marquardt, F.: Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014). https://doi.org/10.1103/RevModPhys.86.1391

    Article  ADS  Google Scholar 

  43. James, D., Jerke, J.: Effective Hamiltonian theory and its applications in quantum information. Can. J. Phys. 85(6), 625–632 (2007). https://doi.org/10.1139/p07-060

    Article  ADS  Google Scholar 

  44. Gamel, O., James, D.F.V.: Time-averaged quantum dynamics and the validity of the effective Hamiltonian model. Phys. Rev. A 82, 052106 (2010). https://doi.org/10.1103/PhysRevA.82.052106

    Article  ADS  Google Scholar 

  45. Shao, W., Wu, C., Feng, X.-L.: Generalized James’ effective Hamiltonian method. Phys. Rev. A 95, 032124 (2017). https://doi.org/10.1103/PhysRevA.95.032124

    Article  ADS  MathSciNet  Google Scholar 

  46. Beaudoin, F., Gambetta, J.M., Blais, A.: Dissipation and ultrastrong coupling in circuit QED. Phys. Rev. A 84, 043832 (2011). https://doi.org/10.1103/PhysRevA.84.043832

    Article  ADS  Google Scholar 

  47. Felicetti, S., Pedernales, J.S., Egusquiza, I.L., Romero, G., Lamata, L., Braak, D., Solano, E.: Spectral collapse via two-phonon interactions in trapped ions. Phys. Rev. A 92, 033817 (2015). https://doi.org/10.1103/PhysRevA.92.033817

    Article  ADS  Google Scholar 

  48. Zheng, S.-B.: Dicke-like quantum phase transition and vacuum entanglement with two coupled atomic ensembles. Phys. Rev. A 84, 033817 (2011). https://doi.org/10.1103/PhysRevA.84.033817

    Article  ADS  Google Scholar 

  49. Ian, H., Gong, Z.R., Liu, Y.-X., Sun, C.P., Nori, F.: Cavity optomechanical coupling assisted by an atomic gas. Phys. Rev. A 78, 013824 (2008). https://doi.org/10.1103/PhysRevA.78.013824

    Article  ADS  Google Scholar 

  50. Chen, X.-Y., Zhang, Y.-Y.: Finite-size scaling analysis in the two-photon Dicke model. Phys. Rev. A 97, 053821 (2018). https://doi.org/10.1103/PhysRevA.97.053821

    Article  ADS  Google Scholar 

  51. Garbe, L., Egusquiza, I.L., Solano, E., Ciuti, C., Coudreau, T., Milman, P., Felicetti, S.: Superradiant phase transition in the ultrastrong-coupling regime of the two-photon Dicke model. Phys. Rev. A 95, 053854 (2017). https://doi.org/10.1103/PhysRevA.95.053854

    Article  ADS  Google Scholar 

  52. Garraway, B.M.: The dicke model in quantum optics: Dicke model revisited. Philos. Trans. R. Soc. A 369(1939), 1137–1155 (2011). https://doi.org/10.1098/rsta.2010.0333

    Article  ADS  MathSciNet  Google Scholar 

  53. Lü, X.-Y., Wu, Y., Johansson, J.R., Jing, H., Zhang, J., Nori, F.: Squeezed optomechanics with phase-matched amplification and dissipation. Phys. Rev. Lett. 114, 093602 (2015). https://doi.org/10.1103/PhysRevLett.114.093602

    Article  ADS  Google Scholar 

  54. Ma, K.K.W., Law, C.K.: Three-photon resonance and adiabatic passage in the large-detuning Rabi model. Phys. Rev. A 92, 023842 (2015). https://doi.org/10.1103/PhysRevA.92.023842

    Article  ADS  Google Scholar 

  55. Enzian, G., et al.: Optica 6, 7 (2019). https://doi.org/10.1364/OPTICA.6.000007

    Article  ADS  Google Scholar 

  56. Pirkkalainen, J.M., Cho, S.U., et al.: Cavity optomechanics mediated by a quantum two-level system. Nat. Commun. 6(6981), 1 (2015). https://doi.org/10.1038/ncomms7981

    Article  Google Scholar 

  57. Niemczyk, T., Deppe, F., et al.: Circuit quantum electrodynamics in the ultrastrong-coupling regime. Nat. Phys. 6(10), 772 (2010). https://doi.org/10.1038/nphys1730

    Article  Google Scholar 

  58. Mirhosseini, M., Sipahigil, A., et al.: Superconducting qubit to optical photon transduction. Nature 588(7839), 599 (2020). https://doi.org/10.1038/s41586-020-3038-6

    Article  ADS  Google Scholar 

  59. Clerk, A.A., Lehnert, K.W., et al.: Hybrid quantum systems with circuit quantum electrodynamics. Nat. Phys. 16(3), 257 (2020). https://doi.org/10.1038/s41567-020-0797-9

    Article  Google Scholar 

  60. Bienfait, A.: Phonon-mediated quantum state transfer and remote qubit entanglement. Science 364(6438), 368 (2019). https://doi.org/10.1126/science.aaw8415

    Article  ADS  Google Scholar 

  61. O’Connell, A.D., Hofheinz, M., et al.: Quantum ground state and single-phonon control of a mechanical resonator. Nature 464(7289), 697 (2010). https://doi.org/10.1038/nature08967

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China under Grant No. 12074070, and the Natural Science Foundation of Fujian Province under Grant No. 2020J01471.

Author information

Author notes

  1. These authors contributed equally to this work.

Authors and Affiliations

  1. Fujian Key Laboratory of Quantum Information and Quantum Optics, College of Physics and Information Engineering, Fuzhou University, Fuzhou, 350108, Fujian, People’s Republic of China

    Zi-Liang Lan, Ya-Wen Chen, Lü-Yun Cheng, Lei Chen, Sai-Yun Ye & Zhi-Rong Zhong

  2. Department of Physics, Fuzhou University, Fuzhou, 350002, People’s Republic of China

    Zi-Liang Lan, Ya-Wen Chen, Lü-Yun Cheng, Lei Chen, Sai-Yun Ye & Zhi-Rong Zhong

Authors
  1. Zi-Liang Lan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ya-Wen Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Lü-Yun Cheng
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Lei Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Sai-Yun Ye
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Zhi-Rong Zhong
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Sai-Yun Ye.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lan, ZL., Chen, YW., Cheng, LY. et al. Dynamical Casimir effect in a hybrid cavity optomechanical system. Quantum Inf Process 23, 72 (2024). https://doi.org/10.1007/s11128-024-04267-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-024-04267-3

Keywords