Skip to main content

Advertisement

Springer Nature Link
Log in

Secure mutual authentication quantum key agreement scheme for two-party setting with key recycling

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

Information-theoretically secure authentication is necessary to guarantee both the authenticity and integrity of the data transferred over the channel in quantum key agreement (QKA). Generally speaking, QKA uses quantum resources to negotiate a unique shared key for every communication; consequently, as the number of communications rises, so does the quantity of quantum key resources used. A secure mutual authentication QKA scheme for the two-party setting with key recycling is proposed, based on single-photon states and Bell states, to realize mutual authentication and minimize quantum key consumption. The proposed protocol generates symmetric keys and authenticates each other using quantum states. Multiple rounds of communication can be accomplished with different keys when combined with key recycling. Additionally, security analysis and efficiency comparison show that our scheme can achieve desirable results with existing quantum technologies.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

The authors confirm that the data supporting the findings of this study are available within the article.

References

  1. Li, X.-Y., Zhao, Y.-L., Nag, A., et al.: Key-recycling strategies in quantum-key-distribution networks. Appl. Sci. 10(11), 3734 (2020)

    Article  Google Scholar 

  2. Shor, P.W.: Algorithms for quantum computation: discrete logarithms and factoring. In Proceedings 35th Annual Symposium on Foundations of Computer Science, pp. 124–134 (1994)

  3. He, Y.-F., Ma, W.-P.: Two-party quantum key agreement against collective noise. Quantum Inf. Process. 15(12), 5023–5035 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  4. He, Y.-F., Ma, W.-P.: Quantum key agreement protocols with four-qubit cluster states. Quantum Inf. Process. 14(9), 3483–3498 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  5. Shi, R.-H.: Useful equations about bell states and their applications to quantum secret sharing. IEEE Commun. Lett. 24(2), 386–390 (2020)

    Article  Google Scholar 

  6. Song, D., Chen, D.-X.: Quantum key distribution based on random grouping Bell state measurement. IEEE Commun. Lett. 24(7), 1496–1499 (2020)

    Article  Google Scholar 

  7. Kun-Fei, Yu., Yang, C.-W., Liao, C.-H., et al.: Authenticated semi-quantum key distribution protocol using Bell states. Quantum Inf. Process. 13(6), 1457–1465 (2014)

    Article  ADS  MathSciNet  Google Scholar 

  8. Gao, G.: Quantum key distribution by comparing Bell states. Opt. Commun. 281(4), 8876–8879 (2008)

    Article  Google Scholar 

  9. He, Y.-F., Pang, Y.-B., Di, M.: Mutual authentication quantum key agreement protocol based on Bell states. Quantum Inf. Process. 21(8), 290 (2022)

    Article  ADS  MathSciNet  Google Scholar 

  10. Yang, Y.-G., Li, B.-R., Li, D., et al.: New quantum key agreement protocols based on Bell states. Quantum Inf. Process. 18(10), 322 (2019)

    Article  ADS  MathSciNet  Google Scholar 

  11. Cao, H., Ma, W.-P.: Efficient multi-party quantum key agreement protocol based on nonorthogonal quantum entangled pairs. Laser Phys. Lett. 15(9), 095201 (2018)

    Article  ADS  Google Scholar 

  12. Min, S.-Q., Chen, H.-Y., Gong, L.-H.: Novel multi-party quantum key agreement protocol with G-like states and bell states. Int. J. Theor. Phys. 57(6), 1811–1822 (2018)

    Article  MathSciNet  Google Scholar 

  13. Zhou, N., Zeng, G.-H., Xiong, J.: Quantum key agreement protocol. Electron. Lett. 40(18), 1149–1150 (2004)

    Article  ADS  Google Scholar 

  14. Shen, D.-S., Ma, W.-P., Wang, L.-l: Two-party quantum key agreement with four-qubit cluster states. Quantum Inf. Process. 13(10), 2313–2324 (2014)

    Article  ADS  MathSciNet  Google Scholar 

  15. Yang, Y.-G., Gao, S., Li, D., et al.: Two-party quantum key agreement over a collective noisy channel. Quantum Inf. Process. 18(3), 74 (2019)

    Article  ADS  MathSciNet  Google Scholar 

  16. Ye-Feng He, Y.-R., Di Yue, M., et al.: Two-party mutual authentication quantum key agreement protocol. Int. J. Theor. Phys. 61(5), 145 (2022)

    Article  MathSciNet  Google Scholar 

  17. Huang, Xi., Zhang, S.-B., Chang, Y., et al.: Quantum key agreement protocol based on quantum search algorithm. Int. J. Theor. Phys. 60(3), 838–847 (2021)

    Article  MathSciNet  Google Scholar 

  18. Zhu, H.-F., Wang, L.-W., Zhang, Y.-L.: An efficient quantum identity authentication key agreement protocol without entanglement. Quantum Inf. Process. 19(10), 381 (2020)

    Article  ADS  MathSciNet  Google Scholar 

  19. Jiang, S.-X., Fang, L., Fang, X.-J.: Two-party quantum key agreement with six-particle entangled states against collective noise. Int. J. Theor. Phys. 62(10), 235 (2023)

    Article  MathSciNet  Google Scholar 

  20. Yu-Guang, Xu., Wang, C.-N., Cheng, K.-F., et al.: A novel three-party mutual authentication quantum key agreement protocol with GHZ states. Int. J. Theor. Phys. 61(10), 245 (2022)

    Article  MathSciNet  Google Scholar 

  21. Yi-Ting, Wu., Chang, H., Guo, G.-D., et al.: Multi-party quantum key agreement protocol with authentication. Int. J. Theor. Phys. 60(11), 4066–4077 (2021)

    MathSciNet  Google Scholar 

  22. Liu, H.-N., Liang, X.-Q., Jiang, D.-H., et al.: Multi-party quantum key agreement with four-qubit cluster states. Quantum Inf. Process. 18(8), 242 (2019)

    Article  ADS  MathSciNet  Google Scholar 

  23. Zhu, H.-F., Wang, C.-N., Li, Z.-X.: Semi-honest three-party mutual authentication quantum key agreement protocol based on GHZ-like state. Int. J. Theor. Phys. 60(1), 293–303 (2021)

    Article  MathSciNet  Google Scholar 

  24. Ma, X.-Y., Hur, J., Li, Z.-X., et al.: Quantum mutual authentication key agreement scheme using five-qubit entanglement towards different realm architecture. Int. J. Theor. Phys. 60(5), 1933–1948 (2021)

    Article  MathSciNet  Google Scholar 

  25. Fehr, S., Salvail, L.: Quantum authentication and encryption with key recycling. In: Coron, J.S., Nielsen, J. (eds.) Advances in Cryptology – EUROCRYPT 2017. Lecture Notes in Computer Science, vol. 10212. Springer, Cham (2017)

    Google Scholar 

  26. Wegman, M., Carter, L.: New hash functions and their use in authentication and set equality. J. Comput. Syst. Sci. 22(3), 265–279 (1981)

    Article  MathSciNet  Google Scholar 

  27. Rogaway, P.: Bucket hashing and its application to fast message authentication. J. Cryptol. 12, 91–115 (1999)

    Article  MathSciNet  Google Scholar 

  28. Portmann, C.: Key recycling in authentication. IEEE Trans. Inform. Theory. 60(7), 4383–4396 (2014)

    Article  MathSciNet  Google Scholar 

  29. Hayden, P., Leung, D.W., Mayers, D.: The Universal composable security of quantum message authentication with key recyling. arXiv: Quantum Physics, 2016, https://arxiv.org/abs/1610.09434

  30. Fehr, S., Salvail, L.: Quantum authentication and encryption with key recycling. In Proceedings of the Annual International Conference on the Theory, Applications of Cryptographic Techniques, Paris, France, pp. 311–338 (2017)

  31. Li, Q., Zhao, Q., Le, D., et al.: Study on the security of the authentication scheme with key recycling in QKD. Quantum Inf. Process. 15(9), 3815–3831 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  32. Yu-Guang, Xu., Chen, L.-Y., Zhu, H.-F.: Quantum key distribution scheme with key recycling in integrated optical network. Int. J. Theor. Phys. 62(5), 103 (2023)

    Article  MathSciNet  Google Scholar 

  33. Cabello, A.: Quantum key distribution in the Holevo limt. Phys. Rev. Lett. 85(26), 5635–5638 (2000)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work was supported by the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant Nos. KJQN202302401, KJQN202202401, KJQN202202402).

Author information

Authors and Affiliations

  1. Chongqing College of Mobile Communication, Chongqing, 401420, China

    Chaonan Wang

  2. Chongqing Key Laboratory of Public Big Data Security Technology, Chongqing, 401420, China

    Chaonan Wang

  3. Guanghe Middle School, Jining, 272007, China

    Qian Zhang

  4. Artificial Intelligence College, Chongqing Technology and Business University, Chongqing, 400067, China

    Shufan Liang

  5. Software College, Shenyang Normal University, Shenyang, 110034, China

    Hongfeng Zhu

Authors
  1. Chaonan Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Qian Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Shufan Liang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Hongfeng Zhu
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

CW contributed to the conception of the study and wrote the main manuscript text; QZ draw the figure; CW and SL implement the code; HZ helped perform the analysis with constructive discussion; All authors reviewed the manuscript.

Corresponding author

Correspondence to Hongfeng Zhu.

Ethics declarations

Conflict of interest

The authors declared that they have no conflicts of interest to this work.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

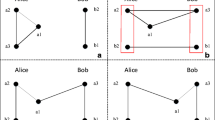
Suppose \(N = 4\), \(K_0 = 0010\), Alice and Bob use \(K_0\) to authenticate each other. The example of MAQKA protocol without considering decoy states, then {\(S_{A1}^1\), \(S_{A2}^1\)} and {\(S_{B1}^1\), \(S_{B2}^1\)} are expressed as follows (The code is available at https://github.com/CNanWang/Secure-MAQKA-for-Two-party, and the execution results have been uploaded as Result_1, Result_2, Result_3, and Result_4):

$$ Alice\left\{ \begin{gathered} S_{A1}^1 :\left\{ {P_{a1}^1 \left( 1 \right),P_{a2}^1 \left( 1 \right),P_{a3}^1 \left( 1 \right),P_{a4}^1 \left( 1 \right)} \right\} \hfill \\ S_{A2}^1 :\left\{ {P_{a1}^1 \left( 2 \right),P_{a2}^1 \left( 2 \right),P_{a3}^1 \left( 2 \right),P_{a4}^1 \left( 2 \right)} \right\} \hfill \\ \end{gathered} \right. \, Bob\left\{ \begin{gathered} S_{B1}^1 :\left\{ {P_{b1}^1 \left( 1 \right),P_{b2}^1 \left( 1 \right),P_{b3}^1 \left( 1 \right),P_{b4}^1 \left( 1 \right)} \right\} \hfill \\ S_{B2}^1 :\left\{ {P_{b1}^1 \left( 2 \right),P_{b2}^1 \left( 2 \right),P_{b3}^1 \left( 2 \right),P_{b4}^1 \left( 2 \right)} \right\} \hfill \\ \end{gathered} \right. $$

{\(K_A^1\), \(OS_A^1\), \(T_A^0\), \(T_A^1\), \(T_A^2\)} and {\(K_B^1\), \(OS_B^1\), \(T_B^0\), \(T_B^1\), \(T_B^2\)} are shown in Tables 

Table 4 The relationship among \(K_A^1\), \(OS_A^1\), \(T_A^0\), \(T_A^1\), and \(T_A^2\)
Full size table

4 and

Table 5 The relationship among \(K_B^1\), \(OS_B^1\), \(T_B^0\), \(T_B^1\) and \(T_B^2\)
Full size table

5, respectively. According to \(T_A^0\), \(T_A^1\), and \(T_A^2\), the detailed process of Alice getting \(K_1\) is as follows:

  1. 1.

    \(\left\{ {T_A^0 \left[ 1 \right] =^{\prime} 00^{\prime} } \right\} = \left\{ {T_A^1 \left[ 1 \right] =^{\prime} 00^{\prime} } \right\}\) and \(\left\{ {T_A^1 \left[ 1 \right] = ^{\prime}00^{\prime}} \right\} \ne \left\{ {T_A^2 \left[ 1 \right] = ^{\prime}10^{\prime}} \right\}\):

    Alice performed Pauli-I operation on \(P_{a1}^1 \left( 2 \right)\), \(OS_A^1 \left[ 1 \right] = I \Leftrightarrow K_A^1 \left[ 1 \right] = 0\);

    Bob performed Pauli-Z operation on \(P_{a1}^1 \left( 2 \right)\), \(OS_B^1 \left[ 1 \right] = Z \Leftrightarrow K_B^1 \left[ 1 \right] = 1\);

  2. 2.

    \(\left\{ {T_A^0 \left[ 2 \right] = ^{\prime}01^{\prime}} \right\} \ne \left\{ {T_A^1 \left[ 2 \right] = ^{\prime}11^{\prime}} \right\}\) and \(\left\{ {T_A^1 \left[ 2 \right] = ^{\prime}11^{\prime}} \right\} \ne \left\{ {T_A^2 \left[ 2 \right] = ^{\prime}01^{\prime}} \right\}\):

    Alice performed Pauli-Z operation on \(P_{a2}^1 \left( 2 \right)\), \(OS_A^1 \left[ 2 \right] = Z \Leftrightarrow K_A^1 \left[ 2 \right] = 1\);

    Bob performed Pauli-Z operation on \(P_{a2}^1 \left( 2 \right)\), \(OS_B^1 \left[ 2 \right] = Z \Leftrightarrow K_B^1 \left[ 2 \right] = 1\);

  3. 3.

    \(\left\{ {T_A^0 \left[ 3 \right] = ^{\prime}11^{\prime}} \right\} = \left\{ {T_A^1 \left[ 3 \right] = ^{\prime}11^{\prime}} \right\}\) and \(\left\{ {T_A^1 \left[ 3 \right] = ^{\prime}11^{\prime}} \right\} = \left\{ {T_A^2 \left[ 3 \right] = ^{\prime}11^{\prime}} \right\}\):

    Alice performed Pauli-I operation on \(P_{a3}^1 \left( 2 \right)\), \(OS_A^1 \left[ 3 \right] = I \Leftrightarrow K_A^1 \left[ 3 \right] = 0\);

    Bob performed Pauli-I operation on \(P_{a3}^1 \left( 2 \right)\), \(OS_B^1 \left[ 3 \right] = I \Leftrightarrow K_B^1 \left[ 3 \right] = 0\);

  4. 4.

    \(\left\{ {T_A^0 \left[ 4 \right] = ^{\prime}11^{\prime}} \right\} \ne \left\{ {T_A^1 \left[ 4 \right] = ^{\prime}01^{\prime}} \right\}\) and \(\left\{ {T_A^1 \left[ 4 \right] = ^{\prime}01^{\prime}} \right\} \ne \left\{ {T_A^2 \left[ 4 \right] = ^{\prime}11^{\prime}} \right\}\):

    Alice performed Pauli-Z operation on \(P_{a4}^1 \left( 2 \right)\), \(OS_A^1 \left[ 4 \right] = Z \Leftrightarrow K_A^1 \left[ 4 \right] = 1\);

    Bob performed Pauli-Z operation on \(P_{a4}^1 \left( 2 \right)\), \(OS_B^1 \left[ 4 \right] = Z \Leftrightarrow K_B^1 \left[ 4 \right] = 1\);

Therefore, Alice gets \(K_B^1 = 1101\) and computes \(K_1 = K_0 \oplus K_A^1 \oplus K_B^1 = 1010\).

According to \(T_B^0\), \(T_B^1\), and \(T_B^2\), the detailed process of Bob getting \(K_1\) is as follows:

  1. 1.

    \(\left\{ {T_B^0 \left[ 1 \right] = ^{\prime}10^{\prime}} \right\} \ne \left\{ {T_B^1 \left[ 1 \right] = ^{\prime}00^{\prime}} \right\}\) and \(\left\{ {T_B^1 \left[ 1 \right] = ^{\prime}00^{\prime}} \right\} = \left\{ {T_B^2 \left[ 1 \right] = ^{\prime}00^{\prime}} \right\}\):

    Bob performed Pauli-Z operation on \(P_{b1}^1 \left( 2 \right)\), \(OS_B^1 \left[ 1 \right] = Z \Leftrightarrow K_B^1 \left[ 1 \right] = 1\);

    Alice performed Pauli-I operation on \(P_{b1}^1 \left( 2 \right)\), \(OS_A^1 \left[ 1 \right] = I \Leftrightarrow K_A^1 \left[ 1 \right] = 0\);

  2. 2.

    \(\left\{ {T_B^0 \left[ 2 \right] = ^{\prime}11^{\prime}} \right\} \ne \left\{ {T_B^1 \left[ 2 \right] = ^{\prime}01^{\prime}} \right\}\) and \(\left\{ {T_B^1 \left[ 2 \right] = ^{\prime}01^{\prime}} \right\} \ne \left\{ {T_B^2 \left[ 2 \right] = ^{\prime}11^{\prime}} \right\}\):

    Bob performed Pauli-Z operation on \(P_{b1}^1 \left( 2 \right)\), \(OS_B^1 \left[ 2 \right] = Z \Leftrightarrow K_B^1 \left[ 2 \right] = 1\);

    Alice performed Pauli-Z operation on \(P_{b1}^1 \left( 2 \right)\), \(OS_A^1 \left[ 2 \right] = Z \Leftrightarrow K_A^1 \left[ 2 \right] = 1\);

  3. 3.

    \(\left\{ {T_B^0 \left[ 3 \right] = ^{\prime}01^{\prime}} \right\} = \left\{ {T_B^1 \left[ 3 \right] = ^{\prime}01^{\prime}} \right\}\) and \(\left\{ {T_B^1 \left[ 3 \right] = ^{\prime}01^{\prime}} \right\} = \left\{ {T_B^2 \left[ 3 \right] = ^{\prime}01^{\prime}} \right\}\):

    Bob performed Pauli-I operation on \(P_{b3}^1 \left( 2 \right)\), \(OS_B^1 \left[ 3 \right] = I \Leftrightarrow K_B^1 \left[ 3 \right] = 0\);

    Alice performed Pauli-I operation on \(P_{b3}^1 \left( 2 \right)\), \(OS_A^1 \left[ 3 \right] = I \Leftrightarrow K_A^1 \left[ 3 \right] = 0\);

  4. 4.

    \(\left\{ {T_B^0 \left[ 4 \right] = ^{\prime}00^{\prime}} \right\} \ne \left\{ {T_B^1 \left[ 4 \right] = ^{\prime}10^{\prime}} \right\}\) and \(\left\{ {T_B^1 \left[ 4 \right] = ^{\prime}10^{\prime}} \right\} \ne \left\{ {T_B^2 \left[ 4 \right] = ^{\prime}00^{\prime}} \right\}\):

    Bob performed Pauli-Z operation on \(P_{b4}^1 \left( 2 \right)\), \(OS_B^1 \left[ 4 \right] = Z \Leftrightarrow K_B^1 \left[ 4 \right] = 1\);

    Alice performed Pauli-Z operation on \(P_{b4}^1 \left( 2 \right)\), \(OS_A^1 \left[ 4 \right] = Z \Leftrightarrow K_A^1 \left[ 4 \right] = 1\);

Therefore, Bob gets \(K_A^1 = 0101\) and computes \(K_1 = K_0 \oplus K_A^1 \oplus K_B^1 = 1010\).

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, C., Zhang, Q., Liang, S. et al. Secure mutual authentication quantum key agreement scheme for two-party setting with key recycling. Quantum Inf Process 23, 139 (2024). https://doi.org/10.1007/s11128-024-04356-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-024-04356-3

Keywords