Skip to main content

Advertisement

Springer Nature Link
Log in

Quantum teleportation scheme using entangled two ququads and its noise effects

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

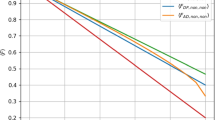
We present a quantum teleportation scheme for single qubits, qutrits, and ququads using maximally entangled pairs of two ququads. Additionally, we demonstrate that, under a specific mapping, single ququad teleportation is equivalent to two-qubit teleportation using generalized Bell states. Furthermore, we establish a dense (superdense) coding scheme for sending four bits of classical information using a single ququad state. We also investigate the efficiency of the single ququad quantum teleportation scheme by studying the fidelity of teleportation when subjected to noise, such as amplitude damping, depolarizing channel, phase damping, and bit flip. Finally, we investigate noise effects in two qubit teleportation and compare its results with the ququad case. We observe that in both cases, adding more noise increases the fidelity of teleportation. Additionally, we show that qubit teleportation is more resilient to noise than ququad teleportation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2000)

    Google Scholar 

  2. Bennett, C.H., Brassard, G., Crépeau, C., Jozsa, R., Peres, A., Wootters, W.K.: Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895–1899 (1993)

    ADS  MathSciNet  Google Scholar 

  3. Bennett, C.H., Wiesner, S.J.: Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states. Phys. Rev. Lett. 69, 2881–2884 (1992)

    ADS  MathSciNet  Google Scholar 

  4. Ekert, A.K.: Quantum cryptography based on bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991)

    ADS  MathSciNet  Google Scholar 

  5. Bennett, C.H., Hayden, P., Leung, D.W., Shor, P.W., Winter, A.: Remote preparation of quantum states. IEEE Trans. Inf. Theory 51(1), 56–74 (2005)

    MathSciNet  Google Scholar 

  6. Deng, F.-G., Long, G.L., Liu, X.-S.: Two-step quantum direct communication protocol using the Einstein-Podolsky-Rosen pair block. Phys. Rev. A 68, 042317 (2003)

    ADS  Google Scholar 

  7. Sheng, Y.-B., Zhou, L., Long, G.-L.: One-step quantum secure direct communication. Sci. Bull. 67(4), 367–374 (2022)

    Google Scholar 

  8. Zhou, L., Sheng, Y.-B.: One-step device-independent quantum secure direct communication. Sci. China Phys. Mech. Astron. 65(5), 250311 (2022)

    ADS  MathSciNet  Google Scholar 

  9. Bouwmeester, D., Pan, J.-W., Mattle, K., Eibl, M., Weinfurter, H., Zeilinger, A.: Experimental quantum teleportation. Nature 390(6660), 575–579 (1997)

    ADS  Google Scholar 

  10. Bao, X.-H., Xiao-Fan, X., Li, C.-M., Yuan, Z.-S., Chao-Yang, L., Pan, J.-W.: Quantum teleportation between remote atomic-ensemble quantum memories. Proc. Natl. Acad. Sci. 109(50), 20347–20351 (2012)

    ADS  Google Scholar 

  11. Furusawa, A., Sorensen, J.L., Braunstein, S.L., Fuchs, C.A., Kimble, H.J., Polzik, E.S.: Unconditional quantum teleportation. Science 282(5389), 706–709 (1998)

    ADS  Google Scholar 

  12. Marcikic, I., De Riedmatten, H., Tittel, W., Zbinden, H., Gisin, N.: Long-distance teleportation of qubits at telecommunication wavelengths. Nature 421(6922), 509–513 (2003)

    ADS  Google Scholar 

  13. Mark Riebe, H., Häffner, CF Roos., Hänsel, W., Benhelm, J., Lancaster, G.P.T., Körber, T.W., Becher, C., Schmidt-Kaler, F., James, D.F.V., et al.: Deterministic quantum teleportation with atoms. Nature 429(6993), 734–737 (2004)

    ADS  Google Scholar 

  14. Steffen, L., Salathe, Y., Oppliger, M., Kurpiers, P., Baur, M., Lang, C., Eichler, C., Puebla-Hellmann, G., Fedorov, A., Wallraff, A.: Deterministic quantum teleportation with feed-forward in a solid state system. Nature 500(7462), 319–322 (2013)

    ADS  Google Scholar 

  15. Rigolin, G.: Quantum teleportation of an arbitrary two-qubit state and its relation to multipartite entanglement. Phys. Rev. A 71, 032303 (2005)

    ADS  Google Scholar 

  16. Shi, B.-S., Tomita, A.: Teleportation of an unknown state by w state. Phys. Lett. A 296(4), 161–164 (2002)

    ADS  MathSciNet  Google Scholar 

  17. Joo, J., Park, Y.-J., Sangchul, O., Kim, J.: Quantum teleportation via a w state. New J. Phys. 5, 136–136 (2003)

    ADS  Google Scholar 

  18. Yeo, Y., Chua, W.K.: Teleportation and dense coding with genuine multipartite entanglement. Phys. Rev. Lett. 96(6), 060502 (2006)

    ADS  Google Scholar 

  19. Muralidharan, S., Panigrahi, P.K.: Perfect teleportation, quantum-state sharing, and superdense coding through a genuinely entangled five-qubit state. Phys. Rev. A 77, 032321 (2008)

    ADS  Google Scholar 

  20. Sheng, Y.-B., Zhou, L.: Demonstration of high-dimensional controlled quantum teleportation for the first time. Sci. China Phys. Mech. Astron. 67(3), 230331 (2024)

    ADS  Google Scholar 

  21. Kim, M.S., Hwang, M.-R., Jung, E., Park, D.K.: Scrambling and quantum teleportation. Quantum Inf. Process. 22(4), 176 (2023)

    ADS  MathSciNet  Google Scholar 

  22. Zhang, Z., Sang, Y.: Bidirectional quantum teleportation in multi-hop communication network. Quantum Inf. Process. 22(5), 201 (2023)

    ADS  MathSciNet  Google Scholar 

  23. Muthukrishnan, A., Stroud, C.R.: Multivalued logic gates for quantum computation. Phys. Rev. A 62, 052309 (2000)

    ADS  MathSciNet  Google Scholar 

  24. Kaszlikowski, D., Gnaciński, P., Żukowski, M., Miklaszewski, W., Zeilinger, A.: Violations of local realism by two entangled \(\mathit{N}\)-dimensional systems are stronger than for two qubits. Phys. Rev. Lett. 85, 4418–4421 (2000)

    ADS  Google Scholar 

  25. Dada, A.C., Leach, J., Buller, G.S., Padgett, M.J., Andersson, E.: Experimental high-dimensional two-photon entanglement and violations of generalized bell inequalities. Nat. Phys. 7(9), 677–680 (2011)

    Google Scholar 

  26. Fickler, R., Lapkiewicz, R., Plick, W.N., Krenn, M., Schaeff, C., Ramelow, S., Zeilinger, A.: Quantum entanglement of high angular momenta. Science 338(6107), 640–643 (2012)

    ADS  Google Scholar 

  27. Erhard, M., Malik, M., Krenn, M., Zeilinger, A.: Experimental greenberger-horne-zeilinger entanglement beyond qubits. Nat. Photon. 12(12), 759–764 (2018)

    ADS  Google Scholar 

  28. Krenn, M., Kottmann, J.S., Tischler, N., Aspuru-Guzik, A.: Conceptual understanding through efficient automated design of quantum optical experiments. Phys. Rev. X 11, 031044 (2021)

    Google Scholar 

  29. Gómez, E.S., Gómez, S., Machuca, I., Cabello, A., Pádua, S., Walborn, S.P., Lima, G.: Multidimensional entanglement generation with multicore optical fibers. Phys. Rev. Appl. 15, 034024 (2021)

    ADS  Google Scholar 

  30. Olislager, L., Mbodji, I., Woodhead, E., Cussey, J., Furfaro, L., Emplit, P., Massar, S., Huy, K.P., Merolla, J.-M.: Implementing two-photon interference in the frequency domain with electro-optic phase modulators. New J. Phys. 14(4), 043015 (2012)

    ADS  Google Scholar 

  31. Bernhard, C., Bessire, B., Feurer, T., Stefanov, A.: Shaping frequency-entangled qudits. Phys. Rev. A 88, 032322 (2013)

    ADS  Google Scholar 

  32. Jin, R.-B., Shimizu, R., Fujiwara, M., Takeoka, M., Wakabayashi, R., Yamashita, T., Miki, S., Terai, H., Gerrits, T., Sasaki, M.: Simple method of generating and distributing frequency-entangled qudits. Quantum Sci. Technol. 1(1), 015004 (2016)

    ADS  Google Scholar 

  33. Martin, A., Guerreiro, T., Tiranov, A., Designolle, S., Fröwis, F., Brunner, N., Huber, M., Gisin, N.: Quantifying photonic high-dimensional entanglement. Phys. Rev. Lett. 118, 110501 (2017)

    ADS  Google Scholar 

  34. Ikuta, T., Takesue, H.: Implementation of quantum state tomography for time-bin qudits. New J. Phys. 19(1), 013039 (2017)

    ADS  Google Scholar 

  35. Luo, Y.-H., Zhong, H.-S., Erhard, M., Wang, X.-L., Peng, L.-C., Krenn, M., Jiang, X., Li, L., Liu, N.-L., Chao-Yang, L., et al.: Quantum teleportation in high dimensions. Phys. Rev. Lett. 123(7), 070505 (2019)

    ADS  Google Scholar 

  36. Xiao-Min, H., Zhang, C., Bi-Heng Liu, Yu., Cai, X.-J.Y., Guo, Yu., Xing, W.-B., Huang, C.-X., Huang, Y.-F., Li, C.-F., Guo, G.-C.: Experimental high-dimensional quantum teleportation. Phys. Rev. Lett. 125, 230501 (2020)

    Google Scholar 

  37. Zhang, C., Chen, J.F., Cui, C., Dowling, J.P., Ou, Z.Y., Byrnes, T.: Quantum teleportation of photonic qudits using linear optics. Phys. Rev. A 100, 032330 (2019)

    ADS  Google Scholar 

  38. Bechmann-Pasquinucci, H., Peres, A.: Quantum cryptography with 3-state systems. Phys. Rev. Lett. 85, 3313–3316 (2000)

    ADS  MathSciNet  Google Scholar 

  39. Bruß, D., Macchiavello, C.: Optimal eavesdropping in cryptography with three-dimensional quantum states. Phys. Rev. Lett. 88, 127901 (2002)

    ADS  Google Scholar 

  40. Cerf, N.J., Bourennane, M., Karlsson, A., Gisin, N.: Security of quantum key distribution using \(\mathit{d}\)-level systems. Phys. Rev. Lett. 88, 127902 (2002)

    ADS  Google Scholar 

  41. Langford, N.K., Dalton, R.B., Harvey, M.D., O’Brien, J.L., Pryde, G.J., Gilchrist, A., Bartlett, S.D., White, A.G.: Measuring entangled qutrits and their use for quantum bit commitment. Phys. Rev. Lett. 93, 053601 (2004)

    ADS  Google Scholar 

  42. Collins, D., Gisin, N., Linden, N., Massar, S., Popescu, S.: Bell inequalities for arbitrarily high-dimensional systems. Phys. Rev. Lett. 88, 040404 (2002)

    ADS  MathSciNet  Google Scholar 

  43. Chamoli, A., Bhandari, C.M.: Teleportation of unknown state by qutrits. Int. J. Quantum Inf. 06(02), 369–378 (2008)

    Google Scholar 

  44. Huang, Y., Yang, W.: Quantum teleportation via qutrit entangled state. Chin. J. Electron. 29(2), 228–232 (2020)

    Google Scholar 

  45. Luo, Y.-H., Zhong, H.-S., Erhard, M., Wang, X.-L., Peng, L.-C., Krenn, M., Jiang, X., Li, L., Liu, N.-L., Chao-Yang, L., Zeilinger, A., Pan, J.-W.: Quantum teleportation in high dimensions. Phys. Rev. Lett. 123, 070505 (2019)

    ADS  Google Scholar 

  46. Al-Amri, M., Evers, J., Suhail Zubairy, M.: Quantum teleportation of four-dimensional qudits. Phys. Rev. A 82, 022329 (2010)

    ADS  Google Scholar 

  47. Werner, R.F.: All teleportation and dense coding schemes. J. Phys. A Math. Gen. 34(35), 7081–7094 (2001)

    ADS  MathSciNet  Google Scholar 

  48. Agrawal, P., Pati, A.: Perfect teleportation and superdense coding with \(w\) states. Phys. Rev. A 74, 062320 (2006)

    ADS  Google Scholar 

  49. Liu, X.S., Long, G.L., Tong, D.M., Li, F.: General scheme for superdense coding between multiparties. Phys. Rev. A 65, 022304 (2002)

    ADS  Google Scholar 

  50. Pati, A.K., Parashar, P., Agrawal, P.: Probabilistic superdense coding. Phys. Rev. A 72, 012329 (2005)

    ADS  Google Scholar 

  51. Wang, C., Deng, F.-G., Li, Y.-S., Liu, X.-S., Long, G.L.: Quantum secure direct communication with high-dimension quantum superdense coding. Phys. Rev. A 71, 044305 (2005)

    ADS  Google Scholar 

  52. Grudka, A., Wójcik, A.: Symmetric scheme for superdense coding between multiparties. Phys. Rev. A 66, 014301 (2002)

    ADS  Google Scholar 

  53. Williams, B.P., Sadlier, R.J., Humble, T.S.: Superdense coding over optical fiber links with complete bell-state measurements. Phys. Rev. Lett. 118, 050501 (2017)

    ADS  Google Scholar 

  54. Xiao-Min, H., Guo, Yu., Liu, B.-H., Huang, Y.-F., Li, C.-F., Guo, G.-C.: Beating the channel capacity limit for superdense coding with entangled ququarts. Sci. Adv. 4(7), eaat9304 (2018)

    ADS  Google Scholar 

  55. Breuer, Heinz-Peter.: Petruccione, Francesco: The Theory of Open Quantum Systems. Oxford University Press, Oxford (2007)

    Google Scholar 

  56. Sangchul, O., Lee, S., Lee, H.: Fidelity of quantum teleportation through noisy channels. Phys. Rev. A 66, 022316 (2002)

    ADS  MathSciNet  Google Scholar 

  57. Li, Y.-L., Chuan-Jin, Z., Wei, D.-M.: Enhance quantum teleportation under correlated amplitude damping decoherence by weak measurement and quantum measurement reversal. Quantum Inf. Process. 18(1), 2 (2018)

    ADS  MathSciNet  Google Scholar 

  58. Fortes, R., Rigolin, G.: Fighting noise with noise in realistic quantum teleportation. Phys. Rev. A 92, 012338 (2015)

    ADS  Google Scholar 

  59. Xueyuan, H., Ying, G., Gong, Q., Guo, G.: Noise effect on fidelity of two-qubit teleportation. Phys. Rev. A 81, 054302 (2010)

    ADS  Google Scholar 

  60. Sebastian, A., Mansar, A.N., Randeep, N.C.: Beyond qubits: an extensive noise analysis for qutrit quantum teleportation. Int. J. Theor. Phys. 62(12), 258 (2023)

    MathSciNet  Google Scholar 

  61. Da-Chuang, L., Zhuo-Liang, C.: Teleportation of two-particle entangled state via cluster state. Commun. Theor. Phys. 47(3), 464–466 (2007)

    ADS  Google Scholar 

  62. Liu, J.-C., Li, Y.-H., Nie, Y.-Y.: Controlled teleportation of an arbitrary two-particle pure or mixed state by using a five-qubit cluster state. Int. J. Theor. Phys. 49(8), 1976–1984 (2010)

    MathSciNet  Google Scholar 

  63. Zheng-Yuan, X., You-Min, Y., Zhuo-Liang, C.: Teleportation of multipartite state via w state. Commun. Theor. Phys. 45(3), 433–436 (2006)

    ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Physics, Government Arts and Science College, Meenchanda, Calicut, Kerala, 673018, India

    N. C. Randeep

  2. Department of Physics, SARBTM Government College, Koyilandy, Kerala, 673307, India

    C. Anukrishna

  3. Department of Physics, AVAH Arts and Science College, Kuluppa, Kozhikode, Kerala, 673523, India

    A. K. Neha Raj

Authors
  1. N. C. Randeep
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. C. Anukrishna
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. A. K. Neha Raj
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to N. C. Randeep.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix A:Quantum circuit for creating generalized Bell states

Appendix A:Quantum circuit for creating generalized Bell states

Figure 9 shows the quantum circuit for creating generalized Bell states. For a given set of input states \(\{|0000\rangle , |1000\rangle , |0100\rangle , |1100\rangle , |0001\rangle , |1001\rangle , |0101\rangle , |1101\rangle ,|0010\rangle , |1010\rangle , |0110\rangle , |1110\rangle , |0011\rangle , |1011\rangle , |0111\rangle , |1111\rangle \} \), this quantum circuit produces 16 maximally entangled four qubit states given by Eq. (15). By applying the mapping described in Eq. (13), the aforementioned four qubit states becomes computational basis state for two ququads denoted by \(\{ \vert aa \rangle , \vert ca \rangle , \vert ba \rangle , \vert da \rangle , \vert ab \rangle , \vert cb \rangle , \) \( \vert bb \rangle , \vert db \rangle , \vert ac \rangle , \vert cc \rangle , \vert bc \rangle , \vert dc \rangle , \vert ad \rangle , \vert cd \rangle , \vert bd \rangle , \vert dd \rangle \}\). Then, applying a unitary transformation equivalent to the quantum circuit shown in Fig. 9 converts the computational basis states of two ququads into maximally entangled states as given by Eq. (4). The inverse circuit (unitary transformation) is useful for generalized Bell measurements.

Fig. 9
figure 9

The quantum circuit for creating four qubit entangled states

Full size image

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Randeep, N.C., Anukrishna, C. & Neha Raj, A.K. Quantum teleportation scheme using entangled two ququads and its noise effects. Quantum Inf Process 23, 192 (2024). https://doi.org/10.1007/s11128-024-04381-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-024-04381-2

Keywords