Abstract
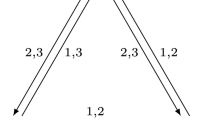
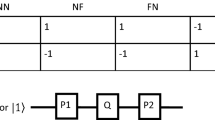
In this research, we investigate the horse racing game, a two-player game with six strategies. Our objective is to develop a theoretical framework for the game by employing the process of quantization. The Nash equilibrium (NE) of the quantum horse racing game is analyzed through an examination of the payoff matrix, and the results are compared to those of the classical horse racing game. Our findings demonstrate that the quantum horse racing game features both pure and mixed strategy NE, whereas the classical horse racing game possesses only mixed strategy NE. Additionally, our results indicate that the quantum horse racing game can mitigate the risks associated with the zero-sum game while outperforming the classical game.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Meyer, D.A.: Quantum strategies. Phys. Rev. Lett. 82, 1052–1055 (1999)
Eisert, J., Wilkens, M., Lewenstein, M.: Quantum games and quantum strategies. Phys. Rev. Lett. 83, 3077–3080 (1999)
Marinatto, L., Weber, T.: Quantum approach to static games of complete information. Phys. Lett. A 272, 291–303 (2000)
Du, J.F., Li, H., Xu, X.D., et al.: Experimental realization of quantum games on a quantum computer. Phys. Rev. Lett. 88, 137902 (2002)
Jing, L., Zhou, L., Kuang, L.M.: Linear optics implementation for quantum game with two players. Phys. Lett. A 330, 48–53 (2004)
Zhou, L., Kuang, L.M.: Proposal for optically realizing quantum game. Phys. Lett. A 315, 426–430 (2003)
Muhammad, S., Tavakoli, A., et al.: Quantum bidding in bridge. Phys. Rev. 4, 021047 (2014)
Benjamin, S.C., Hayden, P.M.: Multiplayer quantum games. Phys. Rev. A 64, 030301(R) (2001)
Iqbal, A., Toor, A.H.: Quantum mechanics gives stability to nash equilibrium. Phys. Rev. A 65, 022306 (2002)
Brassard, G., Broadbent, A., Tapp, A.: Quantum pseudo-telepathy. Foundation Phys 35, 1877–1907 (2004)
Oliveira, D.S., Sousa, P.B.M., Ramos, R. V.: Quantum search algorithm using quantum bit string comparator, International Telecommunications Symposium, Fortaleza, Brazil, 582–585 (2006).
Li, H., Du, J.F., Massar, S.: Continuous-variable quantum games. Phys. Lett. A 306, 73–78 (2002)
Khan, S., Ramzan, M., Khan, M.K.: Quantum model of bertrand duopoly. Chin. Phys. Lett. 27, 080302 (2010)
FraCkiewicz, P., Sladkowski, J.: Quantum approach to bertrand duopoly. Q. Inf. Proc 15, 3637–3650 (2016)
Khan, F.S., Solmeyer, N., Balu, R., Humble, T.S.: Quantum games: A review of the history, current state and interpretation. Q. Inf. Proc 17, 309 (2018)
Agarwal, G.S., Puri, R.R., Singh, R.P.: Atomic Schro Èdinger cat states. Phys. Rev. A 56(3), 2249 (1997)
Henderson, L., Vedral, L.: Classical, quantum and total correlations. J. Phys. A: Math. Gen. 34, 6899 (2001)
Consuelo-Leal, A., Araujo-Ferreira, A.G., Vidoto, E.L.G., Lucas-Oliveira, E., Bonagamba, T.J., Auccaise, R.: NMR Hamiltonian as an effective Hamiltonian to generate Schrödinger’s cat states. Q. Inf. Proc 21, 265 (2022)
Acknowledgements
This project was supported by funding from the Natural Science Foundation of Zhejiang Province (Grant No. LY19A050004).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Chen, J. Quantum horse racing game. Quantum Inf Process 23, 186 (2024). https://doi.org/10.1007/s11128-024-04401-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-024-04401-1