Skip to main content
Springer Nature Link
Log in

An exact quantum logarithmic time algorithm for the 3-junta problem

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

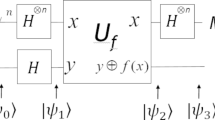
To tackle the \(3\)-junta problem, this work provides an exact quantum learning algorithm for discovering three dependent variables. A 3-junta is a Boolean function \(f:{\left\{\text{0,1}\right\}}^{n}\to \left\{0, 1\right\}\) that is dependent on just three of the \(n\) variables. Chen suggested an exact quantum learning method in 2021 for solving the 3-junta problem with one uncomplemented product by executing the function operation \(O\left(\text{log}_{2}n\right)\) times in the worst-case. In this work, the modified black-box function is used to solve the \(3\)-junta problem. In the worst-case, our proposed quantum algorithm takes \(O\left(\text{log}_{2}n\right)\) function operations. Furthermore, the average number of function operations is calculated. Our algorithm requires at most \(3.41\) function operations on average.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Lu, Z.Q.: The elements of statistical learning: data mining, inference, and prediction. J. Roy Stat. Soc. Ser. A. 173(3), 693–694 (2010)

    Article  Google Scholar 

  2. Mossel, E., O’Donnell, R., Servedio, R.P.: Learning juntas. Proceedings of the Sixth Annual ACM Conference on Computational Learning Theory, 206–212 (2003)

  3. Guyon, I., Elisseeff, A.: An introduction to variable and feature selection. J. Mach. Learn. Res. 3, 1157–1182 (2003)

    Google Scholar 

  4. Chandrashekar, G., Sahin, F.: A survey on feature selection methods. Comput. Electr. Eng. 40(1), 16–28 (2014)

    Article  Google Scholar 

  5. Barrera-García, J., Cisternas-Caneo, F., Crawford, B., Gómez Sánchez, M., Soto, R.: Feature selection problem and metaheuristics: a systematic literature review about its formulation, evaluation and applications. Biomimetics. 9(1), 9 (2023)

    Article  Google Scholar 

  6. Mossel, E., O’Donnell, R., Servedio, R.P.: Learning functions of k relevant variables. J. Comput. Syst. Sci. 69(3), 421–434 (2004)

    Article  MathSciNet  Google Scholar 

  7. Atıcı, A., Servedio, R.A.: Quantum algorithms for learning and testing juntas. Quantum Inf. Process. 6(5), 323–348 (2007)

    Article  ADS  MathSciNet  Google Scholar 

  8. Floess, D.F., Andersson, E., Hillery, M.: Quantum algorithms for testing Boolean functions. https://arxiv.org/abs/1006.1423 (2010).

  9. Bernstein, E., Vazirani, U.: Quantum complexity theory. SIAM J. Comput. 26(5), 1411–1473 (1997)

    Article  MathSciNet  Google Scholar 

  10. Boyer, M., Brassard, G., Høyer, P., Tapp, A.: Tight bounds on quantum searching. Fortsch Phys. -Prog Phys. 46(4–5), 493–505 (1998)

    Article  ADS  Google Scholar 

  11. Ambainis, A., Belovs, A., Regev, O., de Wolf, R.: Efficient quantum algorithms for (gapped) group testing and junta testing. In: Proceedings of the 2016 Annual ACM-SIAM Symposium on Discrete Algorithms, 903–922 (2016)

  12. El-Wazan, K., Younes, A., Doma, S.B.: A quantum algorithm for testing juntas in boolean functions. https://arxiv.org/quant-ph/1701.02143 (2017).

  13. Chen, C.-Y.: An exact quantum algorithm for testing boolean functions with one uncomplemented product of two variables. Quantum Inf. Process. 19(7), 213 (2020)

    Article  ADS  MathSciNet  Google Scholar 

  14. Younes, A.: A fast quantum algorithm for the affine boolean function identification. Eur. Phys. J. Plus. 130(2), 34 (2015)

    Article  Google Scholar 

  15. Chen, C.-Y.: An exact quantum algorithm for testing 3-junta in boolean functions with one uncomplemented product. Quantum Inf. Process. 20(1), 36 (2021)

    Article  ADS  MathSciNet  Google Scholar 

  16. Chen, C.-Y.: An exact quantum algorithm for the 2-junta problem. Int. J. Theor. Phys. 60(1), 80–91 (2021)

    Article  ADS  MathSciNet  Google Scholar 

  17. Chen, C.-Y.: An exact quantum learning algorithm for the 2-junta problem in constant time. Int. J. Theor. Phys. 61(8), 1–9 (2022)

    Article  ADS  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work was supported in part by the National Science and Technology Council of the Republic of China under contract NSTC 112-2221-E-390-013.

Author information

Authors and Affiliations

  1. Department of Computer Science and Information Engineering, National University of Kaohsiung, No.700, Kaohsiung University Rd, Kaohsiung, Taiwan

    Chien-Yuan Chen

Authors
  1. Chien-Yuan Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Chien-Yuan Chen.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, CY. An exact quantum logarithmic time algorithm for the 3-junta problem. Quantum Inf Process 23, 232 (2024). https://doi.org/10.1007/s11128-024-04402-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-024-04402-0

Keywords