Abstract
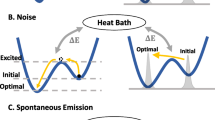
The BBBV theorem is known to largely prohibit exponential speedup of quantum search over classical search, though not entirely, with potential loopholes such as adiabatic quantum computing. Recently, Chen-Huang-Preskill-Zhou (CHPZ) quantum (thermal) gradient descent proposal suggested another potential way to go around the BBBV theorem. We simplify the heavily complicated CHPZ analysis by focusing on the final equilibrium in the quantum thermal operation framework that has already been rigorously formulated in quantum thermodynamics, resulting in quantum thermal search. In particular, repeated applications of an identical quantum mixing thermal operation result in exponential convergence (in the number of repeated applications) of the system state to the equilibrium Gibbs state for the given system Hamiltonian at initial bath temperature. This allows for an efficient computation of the system ground state. Quantum mixing thermal operations evade the BBBV theorem by transferring initial system state information to the bath. Despite computational advantage of CHPZ and quantum thermal search for computing the ground state, it is also noted that some ground state computations corresponding to NP decision problems may require bath states that are exponentially close to the bath ground state, which translates to polynomially-scaling inverse bath temperature, potentially limiting usefulness of quantum thermal search. Potential implications for black hole physics, in light of pure to mixed and back to pure state evolution, are briefly noted.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Allahverdyan, A.E., Petrosyan, D.: Dissipative search of an unstructured database. Phys. Rev. A (2022). https://doi.org/10.1103/physreva.105.032447
Almheiri, A., Mahajan, R., Juan M. & Ying Z.: The page curve of Hawking radiation from semiclassical geometry. J. High Energy Phys. 3, 149 (2020). https://doi.org/10.1007/JHEP03(2020)149
Bennett, Charles H., Bernstein, Ethan, Brassard, Gilles, Vazirani, Umesh: Strengths and weaknesses of quantum computing. SIAM J. Comput. 26(5), 1510–1523 (1997). https://doi.org/10.1137/S0097539796300933
Brandão, F.G., Horodecki, M.S.L., Oppenheim, J., Renes, J.M., Spekkens, R.W.: Resource theory of quantum states out of thermal equilibrium. Phys. Rev. Lett. (2013). https://doi.org/10.1103/physrevlett.111.250404
Brassard, G., Hoyer, P.: An exact quantum polynomial-time algorithm for Simon’s problem. In: Proceedings of the Fifth Israeli Symposium on Theory of Computing and Systems, pp. 12–23, (1997) https://doi.org/10.1109/ISTCS.1997.595153
Burgarth, D., Chiribella, G., Giovannetti, V., Perinotti, P., Yuasa, K.: Ergodic and mixing quantum channels in finite dimensions. New J. Phys. (2013). https://doi.org/10.1088/1367-2630/15/7/073045
Chen, C.-F., Huang, H.-Y., Preskill, J., Zhou, L.: Local minima in quantum systems. (2023) arXiv:2309.16596
Faist, P., Berta, M., Brandao, F.G.S.L.: Thermodynamic implementations of quantum processes. Commun. Math. Phys. 384(3), 1709–1750 (2021). https://doi.org/10.1007/s00220-021-04107-w
Farhi, Edward, Goldstone, Jeffrey, Gutmann, Sam, Lapan, Joshua, Lundgren, Andrew, Preda, Daniel: A quantum adiabatic evolution algorithm applied to random instances of an NP-complete problem. Science 292(5516), 472–475 (2001). https://doi.org/10.1126/science.1057726
García-Pintos, L.P., Linden, N., Malabarba, L., Artur, S., Short, A.J., Winter, A.: Equilibration time scales of physically relevant observables. Phys. Rev. (2017). https://doi.org/10.1103/physrevx.7.031027
Grover, Lov K.: Quantum computers can search rapidly by using almost any transformation. Phys. Rev. Lett. 80, 4329–4332 (1998). https://doi.org/10.1103/PhysRevLett.80.4329
Hawking, Stephen W.: Particle creation by black holes. Commun. Math. Phys. 43(3), 199–220 (1975). https://doi.org/10.1007/BF02345020
Motta, Mario, Sun, Chong, Tan, Adrian T. K., O’Rourke, Matthew J., Ye, Erika, Minnich, Austin J., Brandão, Fernando G. S. L., Chan, Garnet Kin-Lic.: Determining eigenstates and thermal states on a quantum computer using quantum imaginary time evolution. Nat. Phys. 16(2), 205–210 (2019). https://doi.org/10.1038/s41567-019-0704-4
Movassagh, R., Schenker, J.: Theory of ergodic quantum processes. Phys. Rev. (2021). https://doi.org/10.1103/physrevx.11.041001
Penington, G., Shenker, S.H., Douglas S., & Zhenbin Y.: Replica wormholes and the black hole interior. J. High Energy Phys. 3, 205 (2022). https://doi.org/10.1007/JHEP03(2022)205
Raju, Suvrat: Lessons from the information paradox. Phys. Rep. 943, 1–80 (2022). https://doi.org/10.1016/j.physrep.2021.10.001
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interests
The author(s) have no funding source to declare. Furthermore, there is no Conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Kim, M. Quantum thermal search: computing ground states via quantum mixing thermal operations. Quantum Inf Process 23, 206 (2024). https://doi.org/10.1007/s11128-024-04413-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-024-04413-x