Fully measurement-device-independent two-way quantum key distribution with finite single-photon sources

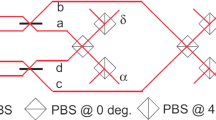
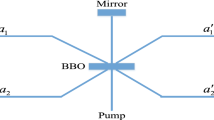
Abstract

Despite the proven security in theory and its potential to achieve high secret key rates, eavesdroppers may crack two-way quantum key distribution (TWQKD) systems by exploiting imperfections of the detection devices that most loopholes exist in, in actual implementations. Lu et al. (Phys. Rev. A 88(4):0443021–044302, 2013) have proved that TWQKD is measurement-device-independent (MDI) security on Bob’s side while assuming ideal detectors on Alice’s side. However, the MDI security proof on Alice’s side is still missing. In this paper, we focus on proving that the TWQKD protocol, secure deterministic communication without entanglement, proposed by Lucamarini and Mancini in 2005 (LM05), is MDI security on both sides of Alice and Bob (fully MDI scenario). First, using a relatively simple method, we give a qubit-based analytical proof that the LM05 is fully MDI security in a depolarizing quantum channel. Then, based on the analytical proof, we derive the expected lower bound of the security formula for it with the reasonable model of finite single-photon sources based on recent experiment progress. Moreover, with the parameters of the current technology, simulation results of the lower bound are presented. It shows that TWQKD can achieve good performances in the fully MDI scenario.

Appendices

Appendix A: Against zero error attacks

For TWQKD protocols, these creative ideas of zero error attacks [24, 25] are fatal and should be dealt with carefully. Here, we analyze the effects of zero error attacks for this fully MDI protocol.

Eve intercepts and stores all of Bob’s qubits $\arrowvert \psi _{Bob}\rangle =\mathop {\otimes }\limits _{i=1}^{N}\arrowvert \phi _{i}\rangle$ on the QFC, and then emits the faked states $\arrowvert \psi _{Eve}\rangle =\mathop {\otimes }\limits _{i=1}^{N}\arrowvert \phi _{i}^{'}\rangle$ to Alice, with the i-th photon $\arrowvert \phi _{i}^{'}\rangle$ randomly chosen from the four states $\left\{ Z:\arrowvert 0\rangle ,\arrowvert 1\rangle ;X:\arrowvert +\rangle ,\arrowvert -\rangle \right\}$. After passing $\arrowvert \psi _{Eve}\rangle$ through the CM(EM) performed by Alice, the faked states $\arrowvert \psi _{Eve}\rangle$ are transformed to $\arrowvert \psi _{Eve}^{'}\rangle$, and Eve tries to extract Alice’s encoding bits $l^{'}_{k}$ by measuring each qubit in $\arrowvert \psi _{Eve}^{'}\rangle$ with the preparation bases of $\arrowvert \psi _{Eve}\rangle$. And then, without changing the position index i, each bit of $l^{'}_{k}$ will be encoded in each of the intercepted qubits $\arrowvert \psi _{Bob}\rangle$. Then $\arrowvert \psi _{Bob}\rangle$ is transformed to $\arrowvert \psi _{Eve}^{''}\rangle$. Finally, with Bob’s bases, Eve measures each qubit of $\arrowvert \psi _{Eve}^{''}\rangle$ and reports the measurement results(classical bits) to Bob. Obviously, via the above attacks, on the one hand, Eve can get all of Alice’s key bits, and on the other hand, Eve will inevitably introduce errors due to the CM. The analysis is simple and presented below. From Tables 1 and 2 in Sect. 2, it is easy to figure out that, in each round, Eve chooses the wrong basis with probability 1/2 when conducting the zero error attacks and sending the faked state $\arrowvert \phi _{i}^{'}\rangle$ to Alice, where she gets a flipped bit 1 with probability 1/2. This strategy will be detected by Alice and Bob after Alice’s announcement in the step.(6) mentioned in Sect. 2, while the measurement result with bit 0 causes zero error. So, considering the fully MDI scenario, before reporting all of the final results to Bob, Eve may, with probability $P_{t}$, tamper with the flipped bit 1, regarded as the result of basis mismatching in the CM, to be 0. However, this strategy causes error in the case that the flipped bit 1 is Alice’s encoding bit since Eve cannot distinguish between the CM and the EM. Hence, the error rates introduced by Eve in the CM and the EM are, respectively, given by

$$\begin{aligned} Q_{f} =(1-P_{t})\cdot \frac{1}{4}P_{c},\nonumber \\ Q_{f-b}=\frac{1}{2}P_{t}\cdot P_{E}, \end{aligned}$$

(A.1)

where $0\le P_{t}\le 1$. Obviously, if Eve does not tamper with any of the flipped bits, the error rate is $Q_{f} =0.0625$. Otherwise, the error rate is $Q_{f-b}=0.375$ if Eve tries to escape completely from being detected by the CM. Hence, Eve should control her strategy to balance $Q_{f}$ and $Q_{f-b}$, while Alice and Bob can set the security threshold bound tightly with $Q_{f-b}=Q_{f}=Q_{(max)}\approx 0.053$, which is true in asymptotic cases in a depolarizing quantum channel to forbid Eve’s zero error attacks.

Appendix B: General collective attacks

In this paper, we consider the case of general collective attacks and classical post-processing implemented with direct reconciliation. The most general attack that Eve can perform on the QFC consists of a joint interaction between the sent qubit and some auxiliary ancillas. It can be represented as

$$\begin{aligned} \widehat{U}\arrowvert i\rangle _{\textbf{k}}\arrowvert \varepsilon \rangle =\arrowvert 0\rangle _{\textbf{k}}\arrowvert \varepsilon _{i0}\rangle +\arrowvert 1\rangle _{\textbf{k}}\arrowvert \varepsilon _{i1}\rangle \qquad i=0,1 , \end{aligned}$$

(B.1)

where $\widehat{U}$(Eve’s attacks operation) is a unitary operation acting on the joint Hilbert space of the ancilla and the qubit $\rho ^{B}$, The set $\left\{ \arrowvert i\rangle _{\textbf{k}}\right\} =\left\{ \arrowvert 0\rangle _{\textbf{k}},\arrowvert 1\rangle _{\textbf{k}} \right\}$ represent the eigenstates of the Pauli operator with $\textbf{k}=\left\{ Z,X \right\}$ Bob’s preparation direction. Without loss of generality, we assume that ancilla states fulfill the following conditions(neglecting the preparation direction symbol $\textbf{k}$)

$$\begin{aligned} \langle \varepsilon _{i0}\arrowvert \varepsilon _{i0}\rangle + \langle \varepsilon _{i1}\arrowvert \varepsilon _{i1}\rangle =1,\nonumber \\ \langle \varepsilon _{00}\arrowvert \varepsilon _{10}\rangle + \langle \varepsilon _{01}\arrowvert \varepsilon _{11}\rangle =0. \end{aligned}$$

(B.2)

Equation(B.2) guarantees the unitarity of $\widehat{U}$. Considering the QFC and QBC are depolarizing channels, the nature noise $Q_{f-b}$ is independent of the bases of the qubit $\rho ^{B}$. Thus, the specific form of Eve’s attacks can further be written as follows

$$\begin{aligned} \langle \varepsilon _{00}\arrowvert \varepsilon _{10}\rangle = \langle \varepsilon _{01}\arrowvert \varepsilon _{11}\rangle =0,\nonumber \\ \langle \varepsilon _{00}\arrowvert \varepsilon _{01}\rangle = \langle \varepsilon _{10}\arrowvert \varepsilon _{11}\rangle =0,\nonumber \\ \langle \varepsilon _{01}\arrowvert \varepsilon _{01}\rangle = \langle \varepsilon _{10}\arrowvert \varepsilon _{10}\rangle =Q_{f-b},\nonumber \\ \langle \varepsilon _{01}\arrowvert \varepsilon _{10}\rangle =0,\langle \varepsilon _{00}\arrowvert \varepsilon _{11}\rangle =1-2Q_{f-b}, \end{aligned}$$

(B.3)

where $Q_{f-b}$ also represents the upper bound of noise that Eve can introduce in her attacks without being detected. According to the Gram matrix defined in Ref. [32] and Eve’s collective attacks $\widehat{U}$ in Eq. (B.1), the sets of the $G\left\{ |\varphi _{1}\rangle ,|\varphi _{2}\rangle ,|\varphi _{3}\rangle ,|\varphi _{4}\rangle \right\}$ can be written as

$$\begin{aligned} \arrowvert \varphi _{1}\rangle =\arrowvert 0\rangle \arrowvert \varepsilon _{00}\rangle +\arrowvert 1\rangle \arrowvert \varepsilon _{01}\rangle ,\nonumber \\ \arrowvert \varphi _{2}\rangle =\arrowvert 0\rangle \arrowvert \varepsilon _{10}\rangle +\arrowvert 1\rangle \arrowvert \varepsilon _{11}\rangle ,\nonumber \\ \arrowvert \varphi _{3}\rangle =iY\arrowvert 0\rangle \arrowvert \varepsilon \rangle =\arrowvert 0\rangle \arrowvert \varepsilon _{01}\rangle -\arrowvert 1\rangle \arrowvert \varepsilon _{00}\rangle ,\nonumber \\ \arrowvert \varphi _{4}\rangle =iY\arrowvert 1\rangle \arrowvert \varepsilon \rangle =\arrowvert 0\rangle \arrowvert \varepsilon _{11}\rangle -\arrowvert 1\rangle \arrowvert \varepsilon _{10}\rangle . \end{aligned}$$

(B.4)

Then, using the specific form of Eve’s attacks in Eq. (B.3), the Gram matrix of $\rho ^{ABE}$ is explicitly given by

$$\begin{aligned} G(\rho ^{ABE})=\frac{1}{4}\begin{pmatrix} 1&{}0&{}0&{}1-2Q_{f-b}\\ 0&{}1&{}2Q_{f-b}-1&{}0\\ 0&{}2Q_{f-b}-1&{}1&{}0\\ 1-2Q_{f-b}&{}0&{}0&{}1\\ \end{pmatrix}. \end{aligned}$$

(B.5)

The eigenvalues of $G(\rho ^{ABE})$ and the von Neumann entropy $S(\rho ^{ABE})$ are, respectively, given by

$$\begin{aligned} \lambda _{1}(\rho ^{ABE})=\frac{1}{2}(1-Q_{f-b}),\lambda _{2}(\rho ^{ABE})=\frac{1}{2}Q_{f-b},\end{aligned}$$

(B.6)

$$\begin{aligned} S(\rho ^{ABE})=-2\left\{ \lambda _{1}(x)log_{2}[\lambda _{1}(x)]+\lambda _{2}(x)log_{2}[\lambda _{2}(x)]\right\} , \end{aligned}$$

(B.7)

where the factor 2 in Eq. (B.7) is due to the multiple roots of the eigenvalues of $G(\rho ^{ABE})$. From Eqs.(B.6), (B.7) and note that $S(\rho ^{ABE})$ takes its maximum S(max) at $\langle \varepsilon _{00}\arrowvert \varepsilon _{10}\rangle =0$, we can get the maximum value of von Neumann entropy $S(\rho ^{ABE})$

$$\begin{aligned} S(\rho _{\lambda _{1,2}}^{ABE})_{max}=1+h(Q_{f-b}). \end{aligned}$$

(B.8)