Skip to main content
Springer Nature Link
Log in

Magnetic field measurement in a hybrid microwave optomechanical-magnetic coupled system

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

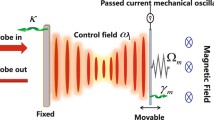
This paper proposes a magnetic field measurement scheme based on a hybrid microwave optomechanical-magnetic coupled system. The proposed sensor comprises a yttrium iron garnet sphere and an optomechanical cavity, where the spring coefficient of the cavity is parametrically modulated. The results demonstrate that the system’s response to the input signal is significantly enhanced, amplifying the weak input signal while reducing the added noise of measurement below the standard quantum limit. Consequently, this hybrid system serves as an effective amplifier, generating a stronger output signal while maintaining sensitivity nearly identical to that of the bare system. We posit that these findings may offer an efficient method for magnetic field measurement and contribute to the advancement of technology in quantum precision measurements.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data Availability

Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

References

  1. Degen, C.L., Reinhard, F., Cappellaro, P.: Quantum sensing. Rev. Mod. Phys. 89, 035002 (2017). https://doi.org/10.1103/RevModPhys.89.035002

    Article  ADS  MathSciNet  Google Scholar 

  2. Yuan, H.Y., Cao, Y., Kamra, A., Duine, R.A., Yan, P.: Quantum magnonics: When magnon spintronics meets quantum information science. Phys. Rep. 965, 1–74 (2022). https://doi.org/10.1016/j.physrep.2022.03.002

    Article  ADS  MathSciNet  Google Scholar 

  3. Rameshti, B.Z., Kusminskiy, S.V., Haigh, J.A., Usami, K., Lachance-Quirion, D., Nakamura, Y., Hu, C.-M., Tang, H.X., Bauer, G.E.W., Blanter, Y.M.: Cavity magnonics. Phys. Rep. 979, 1–61 (2022). https://doi.org/10.1016/j.physrep.2022.06.001

    Article  ADS  MathSciNet  Google Scholar 

  4. Wang, F., Gou, C., Xu, J., Gong, C.: Hybrid magnon-atom entanglement and magnon blockade via quantum interference. Phys. Rev. A 106, 013705 (2022). https://doi.org/10.1103/PhysRevA.106.013705

    Article  ADS  MathSciNet  Google Scholar 

  5. Yu, W., Wang, J., Yuan, H.Y., Xiao, J.: Prediction of attractive level crossing via a dissipative mode. Phys. Rev. Lett. 123, 227201 (2019). https://doi.org/10.1103/PhysRevLett.123.227201

    Article  ADS  Google Scholar 

  6. Zhang, D., Wang, X.-M., Li, T.-F., Luo, X.-Q., Wu, W., Nori, F., You, J.: Cavity quantum electrodynamics with ferromagnetic magnons in a small yttrium-iron-garnet sphere. npj Quant. Inf. 1, 15014 (2015). https://doi.org/10.1038/npjqi.2015.14

    Article  ADS  Google Scholar 

  7. Wolski, S.P., Lachance-Quirion, D., Tabuchi, Y., Kono, S., Noguchi, A., Usami, K., Nakamura, Y.: Dissipation-based quantum sensing of magnons with a superconducting qubit. Phys. Rev. Lett. 125, 117701 (2020). https://doi.org/10.1103/PhysRevLett.125.117701

    Article  ADS  Google Scholar 

  8. Potts, C.A., Bittencourt, V.A.S.V., Kusminskiy, S.V., Davis, J.P.: Magnon-phonon quantum correlation thermometry. Phys. Rev. Appl. 13, 064001 (2020). https://doi.org/10.1103/PhysRevApplied.13.064001

    Article  ADS  Google Scholar 

  9. Ebrahimi, M.S., Motazedifard, A., Harouni, M.B.: Single-quadrature quantum magnetometry in cavity electromagnonics. Phys. Rev. A 103, 062605 (2021). https://doi.org/10.1103/PhysRevA.103.062605

    Article  ADS  MathSciNet  Google Scholar 

  10. Peano, V., Schwefel, H.G.L., Marquardt, C., Marquardt, F.: Intracavity squeezing can enhance quantum-limited optomechanical position detection through deamplification. Phys. Rev. Lett. 115, 243603 (2015). https://doi.org/10.1103/PhysRevLett.115.243603

    Article  ADS  Google Scholar 

  11. Clerk, A.A., Devoret, M.H., Girvin, S.M., Marquardt, F., Schoelkopf, R.J.: Introduction to quantum noise, measurement, and amplification. Rev. Mod. Phys. 82, 1155–1208 (2010). https://doi.org/10.1103/RevModPhys.82.1155

    Article  ADS  MathSciNet  Google Scholar 

  12. Xu, X., Taylor, J.M.: Squeezing in a coupled two-mode optomechanical system for force sensing below the standard quantum limit. Phys. Rev. A 90, 043848 (2014). https://doi.org/10.1103/PhysRevA.90.043848

    Article  ADS  Google Scholar 

  13. Motazedifard, A., Bemani, F., Naderi, M.H., Roknizadeh, R., Vitali, D.: Force sensing based on coherent quantum noise cancellation in a hybrid optomechanical cavity with squeezed-vacuum injection. New J. Phys. 18(7), 073040 (2016). https://doi.org/10.1088/1367-2630/18/7/073040

    Article  ADS  Google Scholar 

  14. Zhang, W.-Z., Han, Y., Xiong, B., Zhou, L.: Optomechanical force sensor in a non-markovian regime. New J. Phys. 19(8), 083022 (2017). https://doi.org/10.1088/1367-2630/aa68d9

    Article  ADS  Google Scholar 

  15. Mason, D., Chen, J., Rossi, M., Tsaturyan, Y., Schliesser, A.: Continuous force and displacement measurement below the standard quantum limit. Nat. Phys. 15, 745–749 (2019). https://doi.org/10.1038/s41567-019-0533-5

    Article  Google Scholar 

  16. Di Giuseppe, G., Vitali, D.: Entangled light enhances force sensing. Nat. Photonics 17, 465–466 (2023). https://doi.org/10.1038/s41566-023-01215-y

    Article  ADS  Google Scholar 

  17. Khalili, F.Y.: Optimal configurations of filter cavity in future gravitational-wave detectors. Phys. Rev. D 81, 122002 (2010). https://doi.org/10.1103/PhysRevD.81.122002

    Article  ADS  Google Scholar 

  18. Caniard, T., Verlot, P., Briant, T., Cohadon, P.-F., Heidmann, A.: Observation of back-action noise cancellation in interferometric and weak force measurements. Phys. Rev. Lett. 99, 110801 (2007). https://doi.org/10.1103/PhysRevLett.99.110801

    Article  ADS  Google Scholar 

  19. Pontin, A., Biancofiore, C., Serra, E., Borrielli, A., Cataliotti, F.S., Marino, F., Prodi, G.A., Bonaldi, M., Marin, F., Vitali, D.: Frequency-noise cancellation in optomechanical systems for ponderomotive squeezing. Phys. Rev. A 89, 033810 (2014). https://doi.org/10.1103/PhysRevA.89.033810

    Article  ADS  Google Scholar 

  20. Clerk, A.A., Marquardt, F., Jacobs, K.: Back-action evasion and squeezing of a mechanical resonator using a cavity detector. New J. Phys. 10(9), 095010 (2008). https://doi.org/10.1088/1367-2630/10/9/095010

    Article  ADS  Google Scholar 

  21. Hertzberg, J.B., Rocheleau, T., Ndukum, T., Savva, M., Clerk, A.A., Schwab, K.C.: Back-action-evading measurements of nanomechanical motion. Nat. Phys. 6, 213–217 (2010). https://doi.org/10.1038/nphys1479

    Article  Google Scholar 

  22. Møller, C.B., Thomas, G. Rodrigo., A. and Vasilakis, Zeuthen, E., Tsaturyan, Y., Balabas, M., Jensen, K., Schliesser, A., Hammerer, K., Polzik, E.S,: Quantum back-action-evading measurement of motion in a negative mass reference frame. Nature 547, 191–195 (2017). https://doi.org/10.1038/nature22980

  23. Ockeloen-Korppi, C.F., Damskägg, E., Pirkkalainen, J.-M., Clerk, A.A., Woolley, M.J., Sillanpää, M.A.: Quantum backaction evading measurement of collective mechanical modes. Phys. Rev. Lett. 117, 140401 (2016). https://doi.org/10.1103/PhysRevLett.117.140401

    Article  ADS  Google Scholar 

  24. de Lépinay, L.M., Ockeloen-Korppi, C.F., Woolley, M.J., Sillanpää, M.A.: Quantum mechanics-free subsystem with mechanical oscillators. Science 372(6542), 625–629 (2021). https://doi.org/10.1126/science.abf5389

    Article  ADS  MathSciNet  Google Scholar 

  25. Bariani, F., Seok, H., Singh, S., Vengalattore, M., Meystre, P.: Atom-based coherent quantum-noise cancellation in optomechanics. Phys. Rev. A 92, 043817 (2015). https://doi.org/10.1103/PhysRevA.92.043817

    Article  ADS  Google Scholar 

  26. Wimmer, M.H., Steinmeyer, D., Hammerer, K., Heurs, M.: Coherent cancellation of backaction noise in optomechanical force measurements. Phys. Rev. A 89, 053836 (2014). https://doi.org/10.1103/PhysRevA.89.053836

    Article  ADS  Google Scholar 

  27. Motazedifard, A., Bemani, F., Naderi, M.H., Roknizadeh, R., Vitali, D.: Force sensing based on coherent quantum noise cancellation in a hybrid optomechanical cavity with squeezed-vacuum injection. New J. Phys. 18(7), 073040 (2016). https://doi.org/10.1088/1367-2630/18/7/073040

    Article  ADS  Google Scholar 

  28. Buchmann, L.F., Schreppler, S., Kohler, J., Spethmann, N., Stamper-Kurn, D.M.: Complex squeezing and force measurement beyond the standard quantum limit. Phys. Rev. Lett. 117, 030801 (2016). https://doi.org/10.1103/PhysRevLett.117.030801

    Article  ADS  Google Scholar 

  29. Khalili, F.Y., Polzik, E.S.: Overcoming the standard quantum limit in gravitational wave detectors using spin systems with a negative effective mass. Phys. Rev. Lett. 121, 031101 (2018). https://doi.org/10.1103/PhysRevLett.121.031101

    Article  ADS  Google Scholar 

  30. Tsang, M., Caves, C.M.: Coherent quantum-noise cancellation for optomechanical sensors. Phys. Rev. Lett. 105, 123601 (2010). https://doi.org/10.1103/PhysRevLett.105.123601

    Article  ADS  Google Scholar 

  31. Tsang, M., Caves, C.M.: Evading quantum mechanics: Engineering a classical subsystem within a quantum environment. Phys. Rev. X 2, 031016 (2012). https://doi.org/10.1103/PhysRevX.2.031016

    Article  Google Scholar 

  32. Allahverdi, H., Motazedifard, A., Dalafi, A., Vitali, D., Naderi, M.H.: Homodyne coherent quantum noise cancellation in a hybrid optomechanical force sensor. Phys. Rev. A 106, 023107 (2022). https://doi.org/10.1103/PhysRevA.106.023107

    Article  ADS  MathSciNet  Google Scholar 

  33. Bemani, F., Černotík, O., Ruppert, L., Vitali, D., Filip, R.: Force sensing in an optomechanical system with feedback-controlled in-loop light. Phys. Rev. Appl. 17, 034020 (2022). https://doi.org/10.1103/PhysRevApplied.17.034020

    Article  ADS  Google Scholar 

  34. Motazedifard, A., Dalafi, A., Naderi, M.H.: Ultraprecision quantum sensing and measurement based on nonlinear hybrid optomechanical systems containing ultracold atoms or atomic Bose-Einstein condensate. AVS Quant. Sci. 3(2), 024701 (2021). https://doi.org/10.1116/5.0035952

    Article  ADS  Google Scholar 

  35. Levitan, B.A., Metelmann, A., Clerk, A.A.: Optomechanics with two-phonon driving. New J. Phys. 18(9), 093014 (2016). https://doi.org/10.1088/1367-2630/18/9/093014

    Article  ADS  Google Scholar 

  36. Motazedifard, A., Dalafi, A., Naderi, M.H.: Negative cavity photon spectral function in an optomechanical system with two parametrically-driven mechanical modes. Opt. Express 31(22), 36615–36637 (2023). https://doi.org/10.1364/OE.499409

    Article  ADS  Google Scholar 

  37. Tabuchi, Y., Ishino, S., Ishikawa, T., Yamazaki, R., Usami, K., Nakamura, Y.: Hybridizing ferromagnetic magnons and microwave photons in the quantum limit. Phys. Rev. Lett. 113, 083603 (2014). https://doi.org/10.1103/PhysRevLett.113.083603

    Article  ADS  Google Scholar 

  38. Tabuchi, Y., Ishino, S., Noguchi, A., Ishikawa, T., Yamazaki, R., Usami, K., Nakamura, Y.: Quantum magnonics: The magnon meets the superconducting qubit. C R Phys. 17(7), 729–739 (2016). https://doi.org/10.1016/j.crhy.2016.07.009.Quantummicrowaves/Micro-ondesquantiques

    Article  ADS  Google Scholar 

  39. Lachance-Quirion, D., Tabuchi, Y., Gloppe, A., Usami, K., Nakamura, Y.: Hybrid quantum systems based on magnonics. Appl. Phys. Express 12(7), 070101 (2019). https://doi.org/10.7567/1882-0786/ab248d

    Article  ADS  Google Scholar 

  40. Baudenbacher, F., Fong, L.E., Holzer, J.R., Radparvar, M.: Monolithic low-transition-temperature superconducting magnetometers for high resolution imaging magnetic fields of room temperature samples. Appl. Phys. Lett. 82(20), 3487–3489 (2003)

    Article  ADS  Google Scholar 

  41. Wan, Q.-M., Lin, Y.-H., Cong, L.-J., Yang, R.-C., Liu, H.-Y.: Quantum entanglement enhanced in hybrid cavity-magnon optomechanical systems. Results Phys. 58, 107449 (2024). https://doi.org/10.1016/j.rinp.2024.107449

    Article  Google Scholar 

  42. Bothner, D., Yanai, S., Iniguez-Rabago, A., Yuan, M., Blanter, Y.M., Steele, G.A.: Cavity electromechanics with parametric mechanical driving. Nat. Commun. 11, 1589 (2020). https://doi.org/10.1038/s41467-020-15389-4

    Article  ADS  Google Scholar 

  43. Szorkovszky, A., Brawley, G.A., Doherty, A.C., Bowen, W.P.: Strong thermomechanical squeezing via weak measurement. Phys. Rev. Lett. 110, 184301 (2013). https://doi.org/10.1103/PhysRevLett.110.184301

    Article  ADS  Google Scholar 

  44. Motazedifard, A., Dalafi, A., Naderi, M.H., Roknizadeh, R.: Controllable generation of photons and phonons in a coupled bose-einstein condensate-optomechanical cavity via the parametric dynamical casimir effect. Ann. Phys. 396, 202–219 (2018). https://doi.org/10.1016/j.aop.2018.07.013

    Article  ADS  Google Scholar 

  45. Li, J., Zhu, S.-Y., Agarwal, G.S.: Magnon-photon-phonon entanglement in cavity magnomechanics. Phys. Rev. Lett. 121, 203601 (2018). https://doi.org/10.1103/PhysRevLett.121.203601

    Article  ADS  Google Scholar 

  46. Zhang, X., Zou, C.-L., Jiang, L., Tang, H.X.: Strongly coupled magnons and cavity microwave photons. Phys. Rev. Lett. 113, 156401 (2014). https://doi.org/10.1103/PhysRevLett.113.156401

    Article  ADS  Google Scholar 

  47. Motazedifard, A., Dalafi, A., Bemani, F., Naderi, M.H.: Force sensing in hybrid bose-einstein-condensate optomechanics based on parametric amplification. Phys. Rev. A 100, 023815 (2019). https://doi.org/10.1103/PhysRevA.100.023815

    Article  ADS  Google Scholar 

  48. Li, Y., Huang, Y.Y., Zhang, X.Z., Tian, L.: Optical directional amplification in a three-mode optomechanical system. Opt. Express 25(16), 18907–18916 (2017). https://doi.org/10.1364/OE.25.018907

    Article  ADS  Google Scholar 

  49. Walls, D.F., Milburn, G.J.: Quantum Optics, 2nd edn. Springer, Berlin (2008)

    Book  Google Scholar 

  50. Clerk, A.A., Devoret, M.H., Girvin, S.M., Marquardt, F., Schoelkopf, R.J.: Introduction to quantum noise, measurement, and amplification. Rev. Mod. Phys. 82, 1155–1208 (2010). https://doi.org/10.1103/RevModPhys.82.1155

    Article  ADS  MathSciNet  Google Scholar 

  51. Schreppler, S., Spethmann, N., Brahms, N., Botter, T., Barrios, M., Stamper-Kurn, D.M.: Optically measuring force near the standard quantum limit. Science 344(6191), 1486–1489 (2014). https://doi.org/10.1126/science.1249850

    Article  ADS  Google Scholar 

  52. Hertzberg, J., Rocheleau, T., Ndukum, T., Savva, M., Clerk, A., Schwab, K.: Back-action evading measurements of nanomechanical motion. Nat. Phys. (2009). https://doi.org/10.1038/nphys1479

    Article  Google Scholar 

  53. Woolley, M.J., Clerk, A.A.: Two-mode back-action-evading measurements in cavity optomechanics. Phys. Rev. A 87, 063846 (2013). https://doi.org/10.1103/PhysRevA.87.063846

    Article  ADS  Google Scholar 

  54. Xu, X., Taylor, J.M.: Squeezing in a coupled two-mode optomechanical system for force sensing below the standard quantum limit. Phys. Rev. A 90, 043848 (2014). https://doi.org/10.1103/PhysRevA.90.043848

    Article  ADS  Google Scholar 

  55. Lucamarini, M., Vitali, D., Tombesi, P.: Scheme for a quantum-limited force measurement with an optomechanical device. Phys. Rev. A 74, 063816 (2006). https://doi.org/10.1103/PhysRevA.74.063816

    Article  ADS  Google Scholar 

  56. Piergentili, P., Li, W., Natali, R., Malossi, N., Vitali, D., Giuseppe, G.D.: Two-membrane cavity optomechanics: non-linear dynamics. New J. Phys. 23(7), 073013 (2021). https://doi.org/10.1088/1367-2630/abdd6a

    Article  ADS  MathSciNet  Google Scholar 

  57. Wang, Z., Kong, F., Zhao, P., Huang, Z., Yu, P., Wang, Y., Shi, F., Du, J.: Picotesla magnetometry of microwave fields with diamond sensors. Sci. Adv. 8(32), 8158 (2022). https://doi.org/10.1126/sciadv.abq8158

    Article  ADS  Google Scholar 

  58. Crescini, N., Carugno, G., Ruoso, G.: Phase-modulated cavity magnon polaritons as a precise magnetic field probe. Phys. Rev. Appl. 16, 034036 (2021). https://doi.org/10.1103/PhysRevApplied.16.034036

    Article  ADS  Google Scholar 

  59. Kleiner, R., Koelle, D., Ludwig, F., Clarke, J.: Superconducting quantum interference devices: State of the art and applications. Proc. IEEE 92(10), 1534–1548 (2004). https://doi.org/10.1109/JPROC.2004.833655

    Article  Google Scholar 

  60. Gallop, J.: Squids: some limits to measurement*. Supercond. Sci. Technol. 16(12), 1575 (2003). https://doi.org/10.1088/0953-2048/16/12/055

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Science, Beijing University of Posts and Telecommunications, Beijing, 100876, People’s Republic of China

    Zhong Ding & Yong Zhang

Authors
  1. Zhong Ding
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yong Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yong Zhang.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ding, Z., Zhang, Y. Magnetic field measurement in a hybrid microwave optomechanical-magnetic coupled system. Quantum Inf Process 23, 323 (2024). https://doi.org/10.1007/s11128-024-04527-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-024-04527-2

Keywords