Skip to main content

Advertisement

Springer Nature Link
Log in

Time dependence of Eisert–Wilkens–Lewenstein quantum game

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

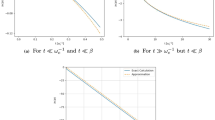
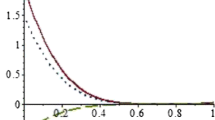
The Eisert–Wilkens–Lewenstein (EWL) game can be used to solve the quantum prisoner’s dilemma is investigated. It is assumed that the states of the players are polarized in different directions, and the entangling gate is time dependent, with interaction strength represented by linear, sine, cosine, or exponential functions. If both players cooperate, the payoffs remain above their classical counterparts. However, if they do not cooperate, the payoff for one player increases at the expense of the other. The payoffs of both players are similar when their states are prepared with the same settings, whereas different settings for the initial states result in different payoffs. Due to the periodic nature of the interaction strength, the payoffs oscillate between their classical bounds when both initial states have the same settings. Conversely, for different initial state, the upper bounds are lower than the classical ones, while the minimum values remain above their corresponding classical payoffs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

The used code of this study is available from the corresponding author upon reasonable request.

References

  1. Alonso-Sanz, R.: Quantum Game Simulation, vol. 36. Springer, New York (2019)

    Google Scholar 

  2. David, A.M.: Quantum strategies. Phys. Rev. Lett. 82, 1052–1055 (1999)

    Article  MathSciNet  Google Scholar 

  3. Eisert, J., Wilkens, M., Lewenstein, M.: Quantum games and quantum strategies. Phys. Rev. Lett. 83, 3077–3080 (1999)

    Article  ADS  MathSciNet  Google Scholar 

  4. Consuelo-Leal, A., Araujo-Ferreira, A.G., Lucas-Oliveira, E., Bonagamba, T.J., Auccaise, R.: Pareto-optimal solution for the quantum battle of the sexes. Quantum Inf. Process. 19, 1–21 (2020)

    Article  ADS  MathSciNet  Google Scholar 

  5. Szopa, M.: Efficiency of classical and quantum games equilibria. Entropy 23(5), 506 (2021)

    Article  ADS  MathSciNet  Google Scholar 

  6. Piotrowski, E.W., Sładkowski, J.: Quantum bargaining games. Physica A 308(1–4), 391–401 (2002)

    Article  ADS  MathSciNet  Google Scholar 

  7. Chen, K.-Y., Hogg, T.: How well do people play a quantum prisoner’s dilemma? Quantum Inf. Process. 5, 43–67 (2006)

    Article  ADS  MathSciNet  Google Scholar 

  8. Piotrowski, E.W.: Quantum auctions: facts and myths. Phys. A 387(15), 3949–3953 (2008)

    Article  MathSciNet  Google Scholar 

  9. Ramzan, M., Khan, M.K.: Environment-assisted quantum minority games. Fluct. Noise Lett. 12(04), 1350025 (2013)

    Article  Google Scholar 

  10. Ikeda, K., Aoki, S.: Theory of quantum games and quantum economic behavior. Quantum Inf. Process. 21(1), 27 (2022)

    Article  ADS  MathSciNet  Google Scholar 

  11. Ning Bao and Nicole Yunger Halpern: Quantum voting and violation of Arrow’s impossibility theorem. Phys. Rev. A 95(6), 062306 (2017)

    Article  ADS  Google Scholar 

  12. Huang, D., Li, S.: Analysis of the quantum evolutionary game of coordination game. Chin. J. Man. Sci. 31(6), 253–264 (2023)

    Google Scholar 

  13. Nguyen, P.-N.: The duality game: a quantum algorithm for body dynamics modeling. Quantum Inf. Process. 23(1), 21 (2024)

    Article  ADS  MathSciNet  Google Scholar 

  14. Gao, M., Ji, Z., Li, T., Wang, Q.: Logarithmic-regret quantum learning algorithms for zero-sum games. Adv. Neur. Inf. 36, (2024)

  15. Jiangfeng, D., Li, H., Xiaodong, X., Shi, M., Jihui, W., Zhou, X., Han, R.: Experimental realization of quantum games on a quantum computer. Phys. Rev. Lett. 88(13), 137902 (2002)

    Article  ADS  Google Scholar 

  16. Mitra, A., Sivapriya, K., Kumar, A.: Experimental implementation of a three qubit quantum game with corrupt source using nuclear magnetic resonance quantum information processor. J. Magn. Reson. 187(2), 306–313 (2007)

    Article  ADS  Google Scholar 

  17. Ulibarrena, A., Sopena, A., Brooks, R., Centeno, D., Ho, J., Sierra, G., Fedrizzi, A.: Photonic implementation of the quantum Morra game. Phys. Rev. Res. 6, 023248 (2024)

    Article  Google Scholar 

  18. Solmeyer, N., Linke, N.M., Figgatt, C., Landsman, K.A., Balu, R., Siopsis, G., Monroe, C.: Demonstration of a Bayesian quantum game on an ion-trap quantum computer. Quantum Sci. Technol. 3(4), 045002 (2018)

    Article  ADS  Google Scholar 

  19. Song, Q., Weiping, F., Wang, W., Sun, Y., Wang, D., Zhou, J.: Quantum decision making in automatic driving. Sci. Rep. 12(1), 11042 (2022)

    Article  ADS  Google Scholar 

  20. Elgazzar, A.S.: Coopetition in quantum prisoner’s dilemma and COVID-19. Quantum Inf. Process. 20(3), 102 (2021)

    Article  ADS  MathSciNet  Google Scholar 

  21. Prafulla Kumar Padhi and Feranando Charrua-Santos: Quantum biotech and internet of virus things: towards a theoretical framework. Appl. Syst. Inn. 4(2), 27 (2021)

    Article  Google Scholar 

  22. Khan, S., Khalid, K.M.: Noisy relativistic quantum games in noninertial frames. Quantum Inf. Process. 12, 1351–1363 (2013)

    Article  ADS  Google Scholar 

  23. Clausen, J., Briegel, H.J.: Quantum machine learning with glow for episodic tasks and decision games. Phys. Rev. A 97, 022303 (2018)

    Article  ADS  Google Scholar 

  24. Abd El-Hakeem EH Abd El-Naby, Elrayes, H.A., Tarabia, A.M.K., Elgazzar, A.S.: Arbitrary maximally entangled quantum prisoner’s dilemma. Z. fur Naturforsch. A, 79(2), 133–140 (2024)

  25. Altintas, A.A., Ozaydin, F., Bayindir, C., Bayrakci, V.: Prisoners’ dilemma in a spatially separated system based on spin-photon interactions. Photonics 9(9), 617 (2022)

    Article  Google Scholar 

  26. Bugu, S., Ozaydin, F., Kodera, T.: Surpassing the classical limit in magic square game with distant quantum dots coupled to optical cavities. Sci. Rep. 10(1), 22202 (2020)

    Article  ADS  Google Scholar 

  27. Ozaydin, F.: Quantum pseudo-telepathy in spin systems: the magic square game under magnetic fields and the Dzyaloshinskii-Moriya interaction. Laser Phys. 30(2), 025203 (2020)

    Article  ADS  Google Scholar 

  28. Elgazzar, A.S.: Unique solution to the quantum prisoner’s dilemma game. J. Phys. Soc. Jpn. 88(3), 034801 (2019)

    Article  ADS  Google Scholar 

  29. He, D., Ye, T.: An improvement of quantum Prisoners’ Dilemma protocol of Eisert–Wilkens–Lewenstein. Int. J. Theor. Phys. 59, 1382–1395 (2020)

    Article  MathSciNet  Google Scholar 

  30. Kameshwari, A.V.S., Balakrishnan, S.: Study of decoherence and memory in modified Eisert–Wilkens–Lewenstein scheme. Quantum Inf. Process. 20, 1–20 (2021)

    Article  MathSciNet  Google Scholar 

  31. Huang, Z., Qiu, D.: Quantum games under decoherence. Int. J. Theor. Phys. 55, 965–992 (2016)

    Article  MathSciNet  Google Scholar 

  32. Tomamichel, M., Fehr, S., Kaniewski, J., Wehner, S.: A monogamy-of-entanglement game with applications to device-independent quantum cryptography. New J. Phys. 15(10), 103002 (2013)

    Article  ADS  MathSciNet  Google Scholar 

  33. Piotrowski, E.W., Sładkowski, J.: Quantum market games. Phys. A 1–2, 208–216 (2002)

    Article  MathSciNet  Google Scholar 

  34. Flitney, A.P., Abbott, D.: Advantage of a quantum player over a classical one in 2\(\times \) 2 quantum games. Proc. R. Soc. Lond. A 459(2038), 2463–2474 (2003)

    Article  ADS  MathSciNet  Google Scholar 

Download references

Acknowledgements

We would like to thank the referees for their reports which help us to modify our manuscript. This work was supported in part by the University of Chinese Academy of Sciences.

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Women for Art, Science and Education, Ain Shams University, Cairo, Egypt

    A. T. M. Makram-Allah

  2. School of Physics, University of Chinese Academy of Science, Yuquan Road 19A, Beijing, 100049, China

    M. Y. Abd-Rabbou

  3. Mathematics Department, Faculty of Science, Al-Azhar University, Nasr City, Cairo, 11884, Egypt

    M. Y. Abd-Rabbou

  4. Mathematics Department College of Science, University of Bahrain, PO Box 320038, Sakhir, Bahrain

    N. Metwally

  5. Department of Mathematics, Aswan University, Aswan, Sahari, 81528, Egypt

    N. Metwally

Authors
  1. A. T. M. Makram-Allah
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. M. Y. Abd-Rabbou
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. N. Metwally
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

ATM prepared all figures and wrote the original draft. MYA-R performed the mathematical calculations. NM reviewed the draft. All authors read and agreed to the published version of the manuscript.

Corresponding author

Correspondence to M. Y. Abd-Rabbou.

Ethics declarations

Ethical approval

The authors declare that there is no conflict with publication ethics.

Conflict of interest

There is no conflict of interest regarding the publication of this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

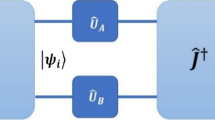
In this appendix, we show the elements of the final state are defined by a \(4\times 4 \) matrix, if the states of the player, Alice and Bob, are defined as \(\bigl | \psi _A(0) \bigr \rangle =\bigl | 0 \bigr \rangle _A\), \(\bigl | \psi _B(0) \bigr \rangle =\bigl | 0 \bigr \rangle _B\), respectively. Then the total initial state of the players is given by (6). If players apply their strategies and send their pairs to the entangling gate, then the players follow the steps described in Sect. 2. Finally, the final state is defined by

$$\begin{aligned} \rho _{11}= & \mathbb {C}_{\theta _A}^2 \mathbb {C}_{\theta _B}^2 (\lambda _{\alpha }^-) ^2 \Bigl [\mathbb {C}^2_{2\tilde{\gamma }} (\lambda _{\alpha }^+)^2+\mathbb {S}^2_{2\tilde{\gamma }}\Bigl ] \Bigl [4 \mathbb {C}_{\tilde{\gamma }}^4+4 \mathbb {C}_{\tilde{\gamma }}^2 \Bigl (\mathbb {S}_{\tilde{\gamma }}^2 (\lambda _{\alpha }^+)^2 -1\Bigl )+1\Bigl ], \\ \rho _{22}= & (\lambda _{\alpha }^-)^2 \Bigl [ e^{i \alpha _A} \mathbb {S}_{\theta _B}A \mathbb {C}_{\theta _B} \mathbb {S}_{2\tilde{\gamma }}( \lambda _{B})\mathbb {C}_{2\tilde{\gamma }}-i \mathbb {C}_{\theta _A} \mathbb {S}_{\theta _B} e^{i (2 \alpha _A+\alpha _B)} \mathbb {C}_{2\tilde{\gamma }} ^2 \\ & +i \mathbb {C}_{\theta _A} \mathbb {S}_{\theta _B} e^{i \alpha _B} \mathbb {S}^2_{2\tilde{\gamma }}\Bigl ]\times \Bigl [ e^{i \alpha _A} \mathbb {S}_{\theta _A} \mathbb {C}_{\theta _B} \mathbb {S}_{2\tilde{\gamma }}(\lambda _{B}) \mathbb {C}_{2\tilde{\gamma }} +i \mathbb {C}_{\theta _A} \mathbb {S}_{\theta _B} e^{i \alpha _B} \mathbb {C}_{2\tilde{\gamma }} ^2\\ & -i \mathbb {C}_{\theta _A} \mathbb {S}_{\theta _B} e^{i (2 \alpha _A+\alpha _B)} \mathbb {S}^2_{2\tilde{\gamma }}\Bigl ], \\ \rho _{33}= & ie^{i \alpha _B} \mathbb {C}_{\theta _A} \mathbb {S}_{\theta _B} \lambda _{A} \mathbb {C}_{2\tilde{\gamma }} -e^{i \alpha _A} \mathbb {S}_{\theta _A} \mathbb {C}_{\theta _B} \Bigl [-4 \mathbb {C}_{\tilde{\gamma }}^2 (1+e^{2 i \alpha _B} \mathbb {S}_{\tilde{\gamma }}^2)+4 \mathbb {C}_{\tilde{\gamma }}^4+1\Bigl ], \\ \rho _{44}= & -(\lambda _{\alpha }^-) ^2 \Bigl [ \mathbb {C}_{\theta _A} \mathbb {C}_{\theta _B}\mathbb {S}_{2\tilde{\gamma }} \mathbb {C}_{2\tilde{\gamma }} \Bigl ((\lambda _{\alpha }^+) ^2 -1\Bigl )-i \mathbb {S}_{\theta _A} \mathbb {S}_{\theta _B}(\lambda _{\alpha }^+)\Bigl ] ^2, \\ \rho _{12}= & \mathbb {C}_{\theta _A} \mathbb {C}_{\theta _B}(\lambda _{\alpha }^-) ^2 \Bigl [(\lambda _{\alpha }^+) ^2 \mathbb {C}^2_{2\tilde{\gamma }}+\mathbb {S}^2_{2\tilde{\gamma }}\Bigl ] \\ & \times \Bigl [ i e^{i \alpha _A} \mathbb {S}_{\theta _A} \mathbb {C}_{\theta _B} \mathbb {S}_{2\tilde{\gamma }}(\lambda _{B}) \mathbb {C}_{2\tilde{\gamma }}- e^{i \alpha _B} \mathbb {S}_{\theta _B} \mathbb {C}_{\theta _A}\Bigl (-4 \mathbb {C}_{\tilde{\gamma }}^2 (1+e^{2 i \alpha _A} \mathbb {S}_{\tilde{\gamma }}^2)+4 \mathbb {C}_{\tilde{\gamma }}^4+1\Bigl )\Bigl ],\\ \rho _{13}= & \mathbb {C}_{\theta _A} \mathbb {C}_{\theta _B}(\lambda _{\alpha }^-) ^2 \Bigl [(\lambda _{\alpha }^+) ^2 \mathbb {C}^2_{2\tilde{\gamma }}+\mathbb {S}^2_{2\tilde{\gamma }}\Bigl ]0 \\ & \times \Bigl [ ie^{i \alpha _B} \mathbb {S}_{\theta _B} \mathbb {C}_{\theta _A} \mathbb {S}_{2\tilde{\gamma }}\lambda _{A}\mathbb {C}_{2\tilde{\gamma }} -e^{i \alpha _A} \mathbb {S}_{\theta _A} \mathbb {C}_{\theta _B} \Bigl (-4 \mathbb {C}_{\tilde{\gamma }}^2 (1+e^{2 i \alpha _B} \mathbb {S}_{\tilde{\gamma }}^2)+4 \mathbb {C}_{\tilde{\gamma }}^4+1\Bigl )\Bigl ], \\ \rho _{14}= & \mathbb {C}_{\theta _A} \mathbb {C}_{\theta _B}(\lambda _{\alpha }^-) ^2 \Bigl [(\lambda _{\alpha }^+) ^2 \mathbb {C}^2_{2\tilde{\gamma }}+\mathbb {S}^2_{2\tilde{\gamma }}\Bigl ]\times \Bigl [ i\mathbb {C}_{\theta _A} \mathbb {C}_{\theta _B} \mathbb {S}_{2\tilde{\gamma }} ((\lambda _{\alpha }^+) ^2-1) \mathbb {C}_{2\tilde{\gamma }}+\mathbb {S}_{\theta _A} \mathbb {S}_{\theta _B} (\lambda _{\alpha }^+)\Bigl ], \\ \rho _{21}= & -\mathbb {C}_{\theta _A} \mathbb {C}_{\theta _B}(\lambda _{\alpha }^-) ^2 \Bigl [4 \mathbb {C}_{\tilde{\gamma }}^4+4 \mathbb {C}_{\tilde{\gamma }}^2 \Bigl ((\lambda _{\alpha }^+) ^2 \mathbb {S}_{\tilde{\gamma }}^2-1\Bigl )+1\Bigl ] \\ & \times \Bigl [ i e^{i \alpha _A} \mathbb {S}_{\theta _A} \mathbb {C}_{\theta _B} (\lambda _{B}) \mathbb {C}_{2\tilde{\gamma }} +\mathbb {C}_{\theta _A} \mathbb {S}_{\theta _B} e^{i (2 \alpha _A+\alpha _B)}\mathbb {C}^2_{2\tilde{\gamma }} - e^{i \alpha _B} \mathbb {C}_{\theta _A} \mathbb {S}_{\theta _B} \mathbb {S}^2_{2\tilde{\gamma }}\Bigl ], \\ \rho _{23}= & (\lambda _{\alpha }^-) ^2 \Bigl [ e^{i \alpha _B} \mathbb {C}_{\theta _A} \mathbb {S}_{\theta _B} \mathbb {S}_{2\tilde{\gamma }}\lambda _{A} \mathbb {C}_{2\tilde{\gamma }} +i e^{i \alpha _A} \mathbb {S}_{\theta _A} \mathbb {C}_{\theta _B} \Bigl (-4 \mathbb {C}_{\tilde{\gamma }}^2 (1+e^{2 i \alpha _B} \mathbb {S}_{\tilde{\gamma }}^2)+4 \mathbb {C}_{\tilde{\gamma }}^4+1\Bigl )\Bigl ] \\ & \times \Bigl [ e^{i \alpha _A} \mathbb {S}_{\theta _A} \mathbb {C}_{\theta _B}\mathbb {S}_{2\tilde{\gamma }}(\lambda _{B}) \mathbb {C}_{2\tilde{\gamma }} -i \mathbb {C}_{\theta _A} \mathbb {S}_{\theta _B} e^{i (2 \alpha _A+\alpha _B)}\mathbb {C}^2_{2\tilde{\gamma }} + ie^{i \alpha _B} \mathbb {C}_{\theta _A} \mathbb {S}_{\theta _B} \mathbb {S}^2_{2\tilde{\gamma }}\Bigl ], \end{aligned}$$
$$\begin{aligned} \rho _{24}= & (\lambda _{\alpha }^-) ^2 \Bigl [2 e^{i \alpha _A} \mathbb {S}_{\theta _A} \mathbb {C}_{\theta _B} \mathbb {S}_{\tilde{\gamma }}\mathbb {C}_{\tilde{\gamma }} (\lambda _{B}) \mathbb {C}_{2\tilde{\gamma }} -i \mathbb {C}_{\theta _A} \mathbb {S}_{\theta _B} e^{i (2 \alpha _A+\alpha _B)}\mathbb {C}^2_{2\tilde{\gamma }}\\ & \times + i e^{i \alpha _B}\mathbb {C}_{\theta _A} \mathbb {S}_{\theta _B} \mathbb {S}^2_{2\tilde{\gamma }}\Bigl ]0 \Bigl [\mathbb {C}_{\theta _A} \mathbb {C}_{\theta _B} \mathbb {S}_{2\tilde{\gamma }} \mathbb {C}_{2\tilde{\gamma }}\Bigl ((\lambda _{\alpha }^+) ^2-1\Bigl ) -i \mathbb {S}_{\theta _A} \mathbb {S}_{\theta _B} (\lambda _{\alpha }^+)\Bigl ], \\ \rho _{31}= & (\lambda _{\alpha }^-) ^2 \mathbb {C}_{\theta _A} \mathbb {C}_{\theta _B} \Bigl [4 \mathbb {C}_{\tilde{\gamma }}^4+4 \mathbb {C}_{\tilde{\gamma }}^2 \Bigl ((\lambda _{\alpha }^+) ^2 \mathbb {S}_{\tilde{\gamma }}^2-1\Bigl )+1\Bigl ] \\ & \times \Bigl [- ie^{i \alpha _B} \mathbb {C}_{\theta _A} \mathbb {S}_{\theta _B} \lambda _{A}\mathbb {C}_{2\tilde{\gamma }} -\mathbb {S}_{\theta _A} \mathbb {C}_{\theta _B} e^{i (\alpha _A+2 \alpha _B)}\mathbb {C}^2_{2\tilde{\gamma }} + e^{i \alpha _A} \mathbb {S}_{\theta _A} \mathbb {C}_{\theta _B} \mathbb {S}^2_{2\tilde{\gamma }}\Bigl ], \\ \rho _{32}= & (\lambda _{\alpha }^-) ^2 \Bigl [ i e^{i \alpha _B}\mathbb {C}_{\theta _A} \mathbb {S}_{\theta _B} \lambda _{A}\mathbb {C}_{2\tilde{\gamma }} +\mathbb {S}_{\theta _A} \mathbb {C}_{\theta _B} e^{i (\alpha _A+2 \alpha _B)}\mathbb {C}^2_{2\tilde{\gamma }} - e^{i \alpha _A} \mathbb {S}_{\theta _A} \mathbb {C}_{\theta _B} \mathbb {S}^2_{2\tilde{\gamma }}\Bigl ] \\ & \times \Bigl [ e^{i \alpha _B}\mathbb {C}_{\theta _A} \mathbb {S}_{\theta _B} \Bigl (-4 \mathbb {C}_{\tilde{\gamma }}^2 (1+e^{2 i \alpha _A} \mathbb {S}_{\tilde{\gamma }}^2)+4 \mathbb {C}_{\tilde{\gamma }}^4+1\Bigl )- i e^{i \alpha _A} \mathbb {S}_{\theta _A} \mathbb {C}_{\theta _B} (\lambda _{B}) \mathbb {C}_{2\tilde{\gamma }} \Bigl ], \\ \rho _{34}= & (\lambda _{\alpha }^-) ^2 \Bigl [ e^{i \alpha _B}\mathbb {C}_{\theta _A} \mathbb {S}_{\theta _B}\mathbb {S}_{2\tilde{\gamma }} \lambda _{A} \mathbb {C}_{2\tilde{\gamma }} -i \mathbb {S}_{\theta _A} \mathbb {C}_{\theta _B} e^{i (\alpha _A+2 \alpha _B)}\mathbb {C}^2_{2\tilde{\gamma }} + i e^{i \alpha _A} \mathbb {S}_{\theta _A} \mathbb {C}_{\theta _B} \mathbb {S}^2_{2\tilde{\gamma }}\Bigl ] \\ & \times \Bigl [ \mathbb {C}_{\theta _A} \mathbb {C}_{\theta _B} \mathbb {C}_{2\tilde{\gamma }} \Bigl ((\lambda _{\alpha }^+) ^2-1\Bigl )-i \mathbb {S}_{\theta _A} \mathbb {S}_{\theta _B} e^{i (\alpha _A+\alpha _B)}\Bigl ], \\ \rho _{41}= & \mathbb {C}_{\theta _A} \mathbb {C}_{\theta _B}(\lambda _{\alpha }^-) ^2 \Bigl [4 \mathbb {C}_{\tilde{\gamma }}^4+4 \mathbb {C}_{\tilde{\gamma }}^2 \Bigl ((\lambda _{\alpha }^+) ^2 \mathbb {S}_{\tilde{\gamma }}^2-1\Bigl )+1\Bigl ]\\ & \times \Bigl [ i \mathbb {C}_{\theta _A} \mathbb {C}_{\theta _B} \mathbb {S}_{2\tilde{\gamma }} \mathbb {C}_{2\tilde{\gamma }}\Bigl ((\lambda _{\alpha }^+) ^2-1\Bigl )+\mathbb {S}_{\theta _A} \mathbb {S}_{\theta _B} (\lambda _{\alpha }^+)\Bigl ],\\ \rho _{42}= & (\lambda _{\alpha }^-) ^2 \Bigl [- e^{i \alpha _A} \mathbb {S}_{\theta _A} \mathbb {C}_{\theta _B} (\lambda _{B})\mathbb {C}_{2\tilde{\gamma }} -i e^{i \alpha _B} \mathbb {C}_{\theta _A} \mathbb {S}_{\theta _B} \Bigl (-4 \mathbb {C}_{\tilde{\gamma }}^2 (1+e^{2 i \alpha _A} \mathbb {S}_{\tilde{\gamma }}^2)+4 \mathbb {C}_{\tilde{\gamma }}^4+1\Bigl )\Bigl ] \\ & \times \Bigl [2 \mathbb {C}_{\theta _A} \mathbb {C}_{\theta _B} \mathbb {C}_{\tilde{\gamma }}S_{\gamma } \mathbb {C}_{2\tilde{\gamma }}\Bigl ((\lambda _{\alpha }^+) ^2-1\Bigl )-i \mathbb {S}_{\theta _A} \mathbb {S}_{\theta _B} (\lambda _{\alpha }^+)\Bigl ], \\ \rho _{43}= & (\lambda _{\alpha }^-) ^2 \Bigl [ ie^{i \alpha _B} \mathbb {C}_{\theta _A} \mathbb {S}_{\theta _B} \mathbb {S}_{2\tilde{\gamma }} \lambda _{A}\mathbb {C}_{2\tilde{\gamma }} -e^{i \alpha _A} \mathbb {S}_{\theta _A} \mathbb {C}_{\theta _B} \Bigl (-4 \mathbb {C}_{\tilde{\gamma }}^2 (1+e^{2 i \alpha _B} \mathbb {S}_{\tilde{\gamma }}^2)+4 \mathbb {C}_{\tilde{\gamma }}^4+1\Bigl )\Bigl ] \\ & \times \Bigl [i \mathbb {C}_{\theta _A} \mathbb {C}_{\theta _B} \mathbb {C}_{2\tilde{\gamma }}\Bigl ((\lambda _{\alpha }^+) ^2-1\Bigl ) +\mathbb {S}_{\theta _A} \mathbb {S}_{\theta _B} (\lambda _{\alpha }^+)\Bigl ]. \end{aligned}$$

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Makram-Allah, A.T.M., Abd-Rabbou, M.Y. & Metwally, N. Time dependence of Eisert–Wilkens–Lewenstein quantum game. Quantum Inf Process 23, 393 (2024). https://doi.org/10.1007/s11128-024-04589-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-024-04589-2

Keywords