Skip to main content
Springer Nature Link
Log in

Parrondo’s paradox in quantum walks with different shift operators

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

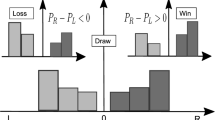
Parrondo’s paradox refers to an unexpected effect when some combination of biased quantum walks shows a counterintuitive inversion of the bias direction. To date this effect was studied in the case of one-dimensional discrete-time quantum walks with deterministic sequences of two or more quantum coins and one shift operator. In the present work, we show that Parrondo’s paradox may also occur for one coin and two different shift operators which create deterministic periodic or aperiodic sequences. Moreover, we demonstrate how Parrondo’s paradox affects the time evolution of the walker-coin quantum entanglement for this kind of quantum walks.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data Availability

Data sharing is not applicable to this article as no data sets were generated or analyzed during the current study.

References

  1. Aharonov, Y., Davidovich, L., Zagury, N.: Quantum random walks. Phys. Rev. A 48, 1687 (1993)

    ADS  Google Scholar 

  2. Farhi, E., Gutmann, S.: Quantum computation and decision trees. Phys. Rev. A 58, 915 (1998)

    ADS  MathSciNet  Google Scholar 

  3. Ambainis, A., Bach, E., Nayak, A., Vishwanath, A., Watrous, J.: One-dimensional quantum walks. In: Proceedings of the 33rd Annual ACM Symposium on Theory of Computing, pp. 37–49 (2001)

  4. Konno, N.: Quantum random walks in one dimension. Quantum Inf. Process. 1, 345 (2002)

    ADS  MathSciNet  Google Scholar 

  5. Kempe, J.: Quantum random walks. Contemp. Phys. 44, 307 (2003)

    ADS  Google Scholar 

  6. Venegas-Andraca, S.E.: Quantum walks: a comprehensive review. Quantum Inf. Process. 11, 1015 (2012)

  7. Manouchehri, K., Wang, J.: Physical Implementation of Quantum Walks. Springer, Berlin (2014)

    Google Scholar 

  8. Portugal, R.: Quantum Walks and Search Algorithms. Springer, Cham (2018)

    Google Scholar 

  9. Neves, L., Puentes, G.: Photonic discrete-time quantum walks and applications. Entropy 20, 731 (2018)

    ADS  MathSciNet  Google Scholar 

  10. Kadian, K., Garhwal, S., Kumar, A.: Quantum walk and its application domains: a systematic review. Comput. Sci. Rev. 41, 100419 (2021)

    MathSciNet  Google Scholar 

  11. Parrondo, J.M.R.: Efficiency of Brownian motors. Workshop of the EEC HC &M Network on Complexity and Chaos (#ERBCHRX-CT940546), ISI Foundation, (Torino, Italy), 1996 (unpublished)

  12. Harmer, G.P., Abbott, D.: Losing strategies can win by Parrondo’s paradox. Nature (London) 402, 864 (1999)

    ADS  Google Scholar 

  13. Parrondo, J.M.R., Harmer, G.P., Abbott, D.: New paradoxical games based on Brownian ratchets. Phys. Rev. Lett. 85, 5226 (2000)

    ADS  Google Scholar 

  14. Parrondo, J.M.R., Dinis, L.: Brownian motion and gambling: from ratchets to paradoxical games. Contemp. Phys. 45, 147 (2004)

    ADS  Google Scholar 

  15. Dinis, L.: Optimal sequence for Parrondo games. Phys. Rev. E 77, 021124 (2008)

    ADS  MathSciNet  Google Scholar 

  16. Toral, R.: Cooperative Parrondo’s games. Fluct. Noise Lett. 1, 7 (2001)

    MathSciNet  Google Scholar 

  17. Dinis, L., Parrondo, J.M.R.: Optimal strategies in collective Parrondo games. Europhys. Lett. 63, 319 (2003)

    ADS  Google Scholar 

  18. Kay, R.J., Johnson, N.F.: Winning combinations of history-dependent games. Phys. Rev. E 67, 056128 (2003)

    ADS  Google Scholar 

  19. Khan, S., Ramzan, M., Khan, M.K.: Quantum Parrondo’s games under decoherence. Int. J. Theor. Phys. 49, 31 (2010)

    MathSciNet  Google Scholar 

  20. Xie, N.-G., Chen, Y., Ye, Y., Xu, G., Wang, L.-G., Wang, C.: Theoretical analysis and numerical simulation of Parrondo’s paradox game in space. Chaos Solitons Fractals 44, 401 (2011)

    ADS  MathSciNet  Google Scholar 

  21. Ye, Y., Xie, N.-G., Wang, L., Cen, Y.-W.: The multi-agent Parrondo’s model based on the network evolution. Physica A 392, 5414 (2013)

    ADS  Google Scholar 

  22. Cheung, K.W., Ma, H.F., Wu, D., Lui, G.C., Szeto, K.Y.: Winning in sequential Parrondo games by players with short-term memory. J. Stat. Mech. Theory Exp. 2016, 054042 (2016)

    MathSciNet  Google Scholar 

  23. Cheong, K.H., Saakian, D.B., Zadourian, R.: Allison mixture and the two-envelope problem. Phys. Rev. E 96, 062303 (2017)

    ADS  Google Scholar 

  24. Koh, J.M., Cheong, K.H.: New doubly-anomalous Parrondo’s games suggest emergent sustainability and inequality. Nonlinear Dyn. 96, 257 (2019)

    Google Scholar 

  25. Koh, J.M., Cheong, K.H.: Generalized solutions of Parrondo’s games. Adv. Sci. 7, 2001126 (2020)

    Google Scholar 

  26. Ye, Y., Zhang, X.-S., Liu, L., Xie, N.-G.: Effects of group interactions on the network Parrondo’s games. Physica A 583, 126271 (2021)

    MathSciNet  Google Scholar 

  27. Lai, J.W., Cheong, K.H.: Boosting Brownian-inspired games with network synchronization. Chaos Solitons Fractals 168, 113136 (2023)

    Google Scholar 

  28. Miszczak, J.A.: Constructing games on networks for controlling the inequalities in the capital distribution. Physica A 594, 126997 (2022)

    MathSciNet  Google Scholar 

  29. Harmer, G.P., Abbott, D.: A review of Parrondo’s paradox. Fluct. Noise Lett. 2, 71 (2002)

    Google Scholar 

  30. Abbott, D.: Asymmetry and disorder: a decade of Parrondo’s paradox. Fluct. Noise Lett. 9, 129 (2010)

    MathSciNet  Google Scholar 

  31. Cheong, K.H., Koh, J.M., Jones, M.C.: Paradoxical survival: examining the Parrondo effect across biology. BioEssays 41, 1900027 (2019)

    Google Scholar 

  32. Lai, J.W., Cheong, K.H.: Social dynamics and Parrondo’s paradox: a narrative review. Nonlinear Dyn. 101, 1 (2020)

    Google Scholar 

  33. Lai, J.W., Cheong, K.H.: Parrondo’s paradox from classical to quantum: A review. Nonlinear Dyn. 100, 849 (2020)

    Google Scholar 

  34. Meyer, D.A., Blumer, H.: Parrondo games as lattice gas automata. J. Stat. Phys. 107, 225 (2002)

    Google Scholar 

  35. Flitney, A.P., Abbott, D., Johnson, N.F.: Quantum walks with history dependence. J. Phys. A 37, 7581 (2004)

    ADS  MathSciNet  Google Scholar 

  36. Košik, J., Miszczak, J.A., Bužek, V.: Quantum Parrondo’s game with random strategies. J. Mod. Opt. 54, 2275 (2007)

    ADS  Google Scholar 

  37. Bulger, D., Freckleton, J., Twamley, J.: Position-dependent and cooperative quantum Parrondo walks. New J. Phys. 10, 093014 (2008)

    ADS  Google Scholar 

  38. Chandrashekar, C.M., Banerjee, S.: Parrondo’s game using a discrete-time quantum walk. Phys. Lett. A 375, 1553 (2011)

    ADS  MathSciNet  Google Scholar 

  39. Flitney, A.P.: Quantum Parrondo’s games using quantum walks. arXiv:1209.2252

  40. Li, M., Zhang, Y.-S., Guo, G.-C.: Quantum Parrondo’s games constructed by quantum random walks. Fluct. Noise Lett. 12, 1350024 (2013)

    Google Scholar 

  41. Pawela, Ł., Sładkowski, J.: Cooperative quantum Parrondo’s games. Phys. D (Amsterdam, Neth.) 256-257, 51 (2013)

  42. Machida, T., Grünbaum, F.A.: Some limit laws for quantum walks with applications to a version of the Parrondo paradox. Quantum Inf. Process. 17, 241 (2018)

    ADS  MathSciNet  Google Scholar 

  43. Rajendran, J., Benjamin, C.: Implementing Parrondo’s paradox with two-coin quantum walks. R. Soc. Open Sci. 5, 171599 (2018)

    ADS  Google Scholar 

  44. Rajendran, J., Benjamin, C.: Playing a true Parrondo’s game with a three-state coin on a quantum walk. Europhys. Lett. 122, 40004 (2018)

    ADS  Google Scholar 

  45. Jan, M., Xu, X.-Y., Wang, Q.-Q., Pan, W.-W., Han, Y.-J., Li, C.-F., Guo, G.C.: Study of Parrondo’s paradox regions in one-dimensional quantum walks. arXiv:2006.16585

  46. Jan, M., Wang, Q.-Q., Xu, X.-Y., Pan, W.-W., Chen, Z., Han, Y.-J., Li, C.-F., Guo, G.-C., Abbott, D.: Experimental realization of Parrondo’s paradox in 1D quantum walks. Adv. Quantum Technol. 3, 1900127 (2020)

    Google Scholar 

  47. Lai, J.W., Tan, J.R.A., Lu, H., Yap, Z.R., Cheong, K.H.: Parrondo paradoxical walk using four-sided quantum coins. Phys. Rev. E 102, 012213 (2020)

    ADS  MathSciNet  Google Scholar 

  48. Lai, J.W., Cheong, K.H.: Parrondo effect in quantum coin-toss simulations. Phys. Rev. E 101, 052212 (2020)

    ADS  MathSciNet  Google Scholar 

  49. Pires, M.A., Duarte Queirós, S.M.: Parrondo’s paradox in quantum walks with time-dependent coin operators. Phys. Rev. E 102, 042124 (2020)

    ADS  MathSciNet  Google Scholar 

  50. Lai, J.W., Cheong, K.H.: Chaotic switching for quantum coin Parrondo’s games with application to encryption. Phys. Rev. Res. 3, 022019 (2021)

    Google Scholar 

  51. Panda, D., Benjamin, C.: Order from chaos in quantum walks on cyclic graphs. Phys. Rev. A 104, 012204 (2021)

    ADS  MathSciNet  Google Scholar 

  52. Walczak, Z., Bauer, J.H.: Parrondo’s paradox in quantum walks with deterministic aperiodic sequence of coins. Phys. Rev. E 104, 064209 (2021)

    ADS  MathSciNet  Google Scholar 

  53. Naves, C.B., Pires, M.A., Soares-Pinto, D.O., Duarte Queirós, S.M.: Enhancing entanglement with the generalized elephant quantum walk from localized and delocalized states. Phys. Rev. A 106, 042408 (2022)

    ADS  Google Scholar 

  54. Panda, D.K., Govind, B.V., Benjamin, C.: Generating highly entangled states via discrete-time quantum walks with Parrondo sequences. Physica A 608, 128256 (2022)

    MathSciNet  Google Scholar 

  55. Trautmann, G., Groiseau, C., Wimberger, S.: Parrondo’s paradox for discrete-time quantum walks in momentum space. Fluct. Noise Lett. 21, 2250053 (2022)

    ADS  Google Scholar 

  56. Walczak, Z., Bauer, J.H.: Parrondo’s paradox in quantum walks with three coins. Phys. Rev. E 105, 064211 (2022)

    ADS  MathSciNet  Google Scholar 

  57. Fang, X.-X., An, K., Zhang, B.-T., Sanders, B.C., Lu, H.: Maximal coin-position entanglement generation in a quantum walk for the third step and beyond regardless of the initial state. Phys. Rev. A 107, 012433 (2023)

    ADS  MathSciNet  Google Scholar 

  58. Jan, M., Khan, N.A., Xianlong, G.: Territories of Parrondo’s paradox and its entanglement dynamics in quantum walks. Eur. Phys. J. Plus 138, 65 (2023)

    Google Scholar 

  59. Mielke, A.: Quantum Parrondo games in low-dimensional Hilbert spaces. arXiv:2306.16845

  60. Naves, C.B., Pires, M.A., Soares-Pinto, D.O., Duarte Queirós, S.M.: Quantum walks in two dimensions: controlling directional spreading with entangling coins and tunable disordered step operator. J. Phys. A 56, 125301 (2023)

    ADS  MathSciNet  Google Scholar 

  61. Walczak, Z., Bauer, J.H.: Noise-induced Parrondo’s paradox in discrete-time quantum walks. Phys. Rev. E 108, 044212 (2023)

    ADS  MathSciNet  Google Scholar 

  62. Kadiri, G.: Scouring Parrondo’s paradox in discrete-time quantum walks. Phys. Rev. A 110, 022421 (2024)

    MathSciNet  Google Scholar 

  63. Cavazzoni, S., Razzoli, L., Ragazzi, G., Bordone, P., Paris, M.G.A.: Coin dimensionality as a resource in quantum metrology involving discrete-time quantum walks. Phys. Rev. A 109, 022432 (2024)

    ADS  MathSciNet  Google Scholar 

  64. Mishra, A., Wen, T., Cheong, K.H.: Parrondo’s paradox in network communication: a routing strategy. Phys. Rev. Res. 6, 012037 (2024)

    Google Scholar 

  65. Razzoli, L., Cenedese, G., Bondani, M., Benenti, G.: Efficient implementation of discrete-time quantum walks on quantum computers. Entropy 26, 313 (2024)

    ADS  Google Scholar 

  66. Ximenes, J.J., Pires, M.A., Villas-Bôas, J.M.: Parrondo’s effect in continuous-time quantum walks. Phys. Rev. A 109, 032417 (2024)

    ADS  Google Scholar 

  67. Meyer, D.A.: From quantum cellular automata to quantum lattice gases. J. Stat. Phys. 85, 551 (1996)

    ADS  MathSciNet  Google Scholar 

  68. Mendonça, J.P., de Moura, F.A.B.F., Lyra, M.L., Almeida, G.M.A.: Emergent nonlinear phenomena in discrete-time quantum walks. Phys. Rev. A 101, 062335 (2020)

    ADS  MathSciNet  Google Scholar 

  69. Gong, L., Guo, X., Sun, J., Cheng, W., Zhao, S.: Wave packet spreading with periodic, Fibonacci quasi periodic, and random nonlinear discrete-time quantum walks. Quantum Inf. Process. 21, 393 (2022)

    ADS  Google Scholar 

  70. Bauer, J.H., Walczak, Z.: Entanglement entropy in a certain nonlinear discrete quantum walk model. Quantum Inf. Process. 23, 118 (2024)

    ADS  MathSciNet  Google Scholar 

  71. Passos, F.S., Buarque, A.R.C.: Nonlinear flip-flop quantum walks through potential barriers. Phys. Rev. A 106, 062407 (2022)

    ADS  Google Scholar 

  72. Abal, G., Siri, R., Romanelli, A., Donangelo, R.: Quantum walk on the line: entanglement and nonlocal initial conditions. Phys. Rev. A 73, 042302 (2006)

    ADS  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Theoretical Physics, Faculty of Physics and Applied Informatics, University of Lodz, Pomorska 149/153, 90-236, Lodz, Poland

    Zbigniew Walczak & Jarosław H. Bauer

Authors
  1. Zbigniew Walczak
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jarosław H. Bauer
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

Z.W. prepared all calculations and figures. J.H.B. wrote the main manuscript text. Both authors reviewed the manuscript.

Corresponding author

Correspondence to Jarosław H. Bauer.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Walczak, Z., Bauer, J.H. Parrondo’s paradox in quantum walks with different shift operators. Quantum Inf Process 23, 408 (2024). https://doi.org/10.1007/s11128-024-04614-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-024-04614-4

Keywords