Skip to main content

Advertisement

Springer Nature Link
Log in

A novel lottery protocol based on quantum blockchain

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

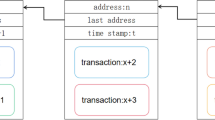
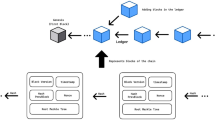
The lottery business is a form of gambling activity operated by authority agencies. Due to the substantial economic interests, its security and fairness become the core elements of industry development. To maintain the trust of participants and ensure fair competition, blockchain technology has been widely applied in the lottery field due to the characteristics of decentralization, transparency, and immutability. However, with the rapid advancement of quantum computing, the security of traditional blockchain technology is challenged largely. To tackle this issue, a novel consensus mechanism which can resist quantum attacks is first proposed, based on a self-tallying quantum voting protocol. Then, a quantum circuit is designed, which can encode n-bit binary information into the relative phase of a quantum state and entangle the blocks by means of controlled-Z (CZ) gate, forming a quantum blockchain structure with timestamps. Finally, utilizing the designed quantum blockchain, a new type of lottery protocol is constructed. The proposed protocol meets the requirements of decentralization, unforgeability, verifiability, and quantum attack resistance. Compared to existing lottery protocols, it can support an arbitrary number of players, and only one communication is required for the ticket purchase process of each player, making it suitable for most of lottery game scenarios.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

Data availability

No datasets were generated or analyzed during the current study.

References

  1. Nakamoto, S.: Bitcoin: A peer-to-peer electronic cash system. Decentralized Business Review. https://nakamotoinstitute.org/library/bitcoin/ (2024)

  2. King, S., Nadal, S.: PPCoin: peer-to-peer crypto-currency with proof-of-stake. Self-Publ. Paper 19(1), 1–6 (2012)

    MATH  Google Scholar 

  3. Larimer, D.: Delegated proof-of-stake (DPoS). Bitshare Whitepaper 81, 85 (2014)

    MATH  Google Scholar 

  4. Miller, V.S.: Use of elliptic curves in cryptography. In: Conference on the theory and application of cryptographic techniques, pp. 417–426. Springer, Berlin (1985)

    MATH  Google Scholar 

  5. Rivest, R.L.: A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 26(2), 96–99 (1978)

    MathSciNet  MATH  Google Scholar 

  6. Shor, P.W.: Algorithms for quantum computation: discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, pp. 124–134 (1994)

  7. Grover, L.K.: Quantum mechanics helps in searching for a needle in a haystack. Phys. Rev. Lett. 79(2), 325–328 (1997)

    Article  ADS  MATH  Google Scholar 

  8. Sayeed, S., Marco-Gisbert, H.: Assessing blockchain consensus and security mechanisms against the 51% attack. Appl. Sci. 9(9), 1788 (2019)

    Article  MATH  Google Scholar 

  9. Jogenfors, J.: Quantum bitcoin: an anonymous and distributed currency secured by the no-cloning theorem of quantum mechanics. In 2019 IEEE International Conference on Blockchain and Cryptocurrency (ICBC), Seoul, Korea (South), pp 245–252 (2019)

  10. Kiktenko, E.O., Pozhar, N.O., Anufriev, M.N., et al.: Quantum-secured blockchain. Quantum Sci. Technol. 3(3), 035004 (2018)

    Article  ADS  MATH  Google Scholar 

  11. Rajan, D., Visser, M.: Quantum blockchain using entanglement in time. Quantum Rep. 1(1), 3–11 (2019)

    Article  MATH  Google Scholar 

  12. Sun, X., Sopek, M., Wang, Q., Kulicki, P.: Towards quantum-secured permissioned blockchain: signature, consensus, and logic. Entropy 21(9), 1–15 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  13. Banerjee, S., Mukherjee, A., Panigrahi, P.K.: Quantum blockchain using weighted hypergraph states. Phys. Rev. Res. 2(1), 013322 (2020)

    Article  MATH  Google Scholar 

  14. El-Latif, A., Abd-El-Atty, B., Mehmood, I., et al.: Quantum-inspired blockchain-based cybersecurity: securing smart edge utilities in IoT-based smart cities. Inf. Process. Manag. 58(4), 10 (2021)

    MATH  Google Scholar 

  15. Wu, F., Zhou, B., Jiang, J., et al.: Blockchain privacy protection based on post-quantum threshold algorithm. Comput. Mater. Contin. 76(1), 1–17 (2023)

    MATH  Google Scholar 

  16. Lin, C., He, D., Huang, X., et al.: DCAP: A secure and efficient decentralized conditional anonymous payment system based on blockchain. IEEE Trans. Inf. Forensics Secur. 15, 2440–2452 (2020)

    Article  MATH  Google Scholar 

  17. Yang, X., Lau, W.F., Ye, Q., et al.: Practical escrow protocol for bitcoin. IEEE Trans. Inf. Forensics Secur. 15, 3023–3034 (2020)

    Article  MATH  Google Scholar 

  18. Truong, N.B., Sun, K., Lee, G.M., Guo, Y.: GDPR-compliant personal data management: a blockchain-based solution. IEEE Trans. Inf. Forensics Secur. 15, 1746–1761 (2020)

    Article  MATH  Google Scholar 

  19. Chow, S.S.M., Hui, L.C.K., Yiu, S., and Chow, K.P.: An e-lottery scheme using verifiable random function. In: Proceedings of the International Conference on Computational Science and its Applications, pp 651–660. Singapore, May 9–12, (2005).

  20. Bentov, I., and Kumaresan, R.: How to use bitcoin to design fair protocols. In Advances in Cryptology—CRYPTO 2014—34th Annual Cryptology Conference, pp 421–439. Santa Barbara, CA, USA, August 17–21 (2014)

  21. Grumbach, S., Riemann, R.: Distributed random process for a large-scale peer-to-peer lottery. In: Distributed applications and interoperable systems, pp. 34–48. Springer International Publishing, Cham (2017)

    Chapter  MATH  Google Scholar 

  22. Miller, A., and Bentov, I.: Zero-collateral lotteries in bitcoin and ethereum. In Proceedings of the 2017 IEEE European Symposium on Security and Privacy Workshops, EuroS&P Workshops 2017, pp. 4–13. Paris, France, 26–28 April (2017)

  23. Goldenberg, L., Vaidman, L., Wiesner, S.: Quantum gambling. Phys. Rev. Lett. 82, 3356–3359 (1999)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  24. Spekkens, R.W., Rudolph, T.: Quantum protocol for cheat-sensitive weak coin flipping. Phys. Rev. Lett. 89, 227901 (2002)

    Article  ADS  MATH  Google Scholar 

  25. Nguyen, A.T., Frison, J., Huy, K.P., Massar, S.: Experimental quantum tossing of a single coin. New J. Phys. 10, 083037 (2008)

    Article  ADS  MATH  Google Scholar 

  26. Hänggi, E., Wullschleger, J.: Tight bounds for classical and quantum coin flipping. In: Theory of cryptography, pp. 468–485. Springer, Berlin/Heidelberg, Germany (2011)

    Chapter  MATH  Google Scholar 

  27. Nayak, A., Sikora, J., Tunçel, L.: A search for quantum coin-flipping protocols using optimization techniques. Math. Program. 156, 581–613 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  28. Sun, X., Sopek, M., Wang, Q., et al.: Towards quantum-secured permissioned blockchain: signature, consensus, and logic. Entropy 21, 887 (2019)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  29. Sun, X., Kulicki, P., Sopek, M.: Lottery and auction on quantum blockchain. Entropy 22(12), 1377 (2020)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  30. Wang, Q., Yu, C., Gao, F., et al.: Self-tallying quantum anonymous voting. Phys. Rev. A 94(2), 022333 (2016)

    Article  ADS  Google Scholar 

  31. Nielsen, M.A., and Chuang, I.L.: Quantum computation and quantum information, pp. 203–208 Cambridge University Press, (2000)

  32. Bennett, C.H., and Brassard, G.: An update on quantum cryptography. In Advances in Cryptology–CRYPTO ’84, pp. 475–480. Santa Barbara, California, USA, August 19–22, (1984)

  33. Lo, H.-K., Ma, X., Chen, K.: Decoy state quantum key distribution. Phys. Rev. Lett. 94(23), 230504 (2005)

    Article  ADS  MATH  Google Scholar 

  34. Li, Q., Wu, J., Quan, J., et al.: Efficient quantum blockchain with a consensus mechanism QDPoS. IEEE Trans. Inf. Forensics Secur. 17, 3264–3276 (2022)

    Article  MATH  Google Scholar 

  35. Weng, C.-X., Gao, R.-Q., Bao, Y., et al.: Beating the fault-tolerance bound and security loopholes for Byzantine agreement with a quantum solution. Research (2022). https://doi.org/10.34133/research.0272

    Article  MATH  Google Scholar 

  36. Song, Y.-Q., Wu, Y.-S., Wu, S.-Y., et al.: A quantum federated learning framework for classical clients. Sci. China-Phys. Mech. Astron. 67, 250311 (2024)

    Article  ADS  MATH  Google Scholar 

  37. Li, L., Li, J., Song, Y.-Q., et al.: An efficient quantum proactive incremental learning algorithm. Sci. China Phys., Mech. Astron. 68, 210313 (2025)

    Article  MATH  Google Scholar 

  38. Song, Y.-Q., Li, J., Wu, Y.-S., et al.: A resource-efficient quantum convolutional neural network. Front. Phys. 12, 1362690 (2024)

    Article  MATH  Google Scholar 

  39. Qin, L.-Z., Liu, B., Gao, F., et al.: Decoy-state quantum private query protocol with two-way communication. Phys. A-Stat. Mech. Appl. 633, 129427 (2024)

    Article  MathSciNet  MATH  Google Scholar 

  40. Li, B.-K., Yang, Y.-G., Wen, Q.-Y.: Threshold quantum secret sharing of secure direct communication. Chin. Phys. Lett. 26(1), 010302 (2009)

  41. Liu, B.-X., Yang, Y.-G., Xu, G.-B., et al.: Heralded quantum network coding of multi-particle states based on quantum time-bin multiplexing. Phys. A. 639, 129683 (2024)

  42. Liu, B.-X., Xu, G.-B., Yang, Y.-G.: Complete security solution for practical quantum network coding. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 43(9), 2692–2704 (2024)

  43. Yang, Y.-G., Teng, Y.-W., Chai, H.-P., Wen, Q.-Y.: Fault-tolerant quantum secret sharing against collective noise. Phys. Scr. 83(2), 025003 (2011)

  44. Yang, Y.-G., Wang, Y., Teng, Y.-W., Chai, H.-P., Wen, Q.-Y.: Scalable arbitrated quantum signature of classical messages with multi-signers. Commun. Theor. Phys. 54(1), 84–88 (2010)

  45. Yang, Y.-G., Chai, H.-P., Teng, Y.-W., Wen, Q.-Y.: Improving the security of controlled quantum secure direct communication by using four particle cluster states against an attack with fake entangled particles. Int. J. Theor. Phys. 50(2), 395–400 (2011)

  46. Yang, Y.-G., Wang, H.-Y., Jia, X., Zhang, H.: A quantum protocol for (t, n)-threshold identity authentication based on Greenberger-Horne-Zeilinger States. Int. J. Theor. Phys. 52(2), 524–530 (2013)

  47. Yang, Y.-G., Cao, W.-F., Wen, Q.-Y.: Three-party quantum secret sharing of secure direct communication based on χ-type entangled states. Chin. Phys. B 19(5), 050306 (2010)

  48. Yang, Y.-G., Wen, Q.-Y.: Threshold quantum secure direct communication without entanglement. Sci. China Ser. G-Phys. Mech. Astron. 51(2), 176–183 (2008)

  49. Yang, Y.-G., Wen, Q.-Y., Zhu, F.-C.: An efficient quantum secret sharing protocol with orthogonal product states. Sci. China Ser. G-Phys. Mech. Astron. 50(3), 331–338 (2007)

  50. Yang, Y.-G., Wen, Q.-Y.: Threshold multiparty quantum-information splitting via quantum channel encryption. Int. J. Quantum Inf. 07(06), 1249–1254 (2009)

  51. Yang, Y.-G., Wen, Q.-Y.: Quantum threshold group signature. Sci. China Ser. G-Phys. Mech. Astron. 51, 1505–1514 (2008)

  52. Yang, Y.-G., Liu, B.-X., Xu, G.-B., et al.: Flexible quantum network coding by using quantum multiplexing. Adv. Quantum Technol. 7(9), 202400016 (2024)

  53. Yang, Y.-G., Sun, S.-J., Xu, P., et al.: Flexible protocol for quantum private query based on B92 protocol. Quantum Inf. Process. 13, 805–813 (2014)

  54. Yang, Y.-G., Liu, B.-X., Xu, G.-B., et al.: Practical quantum anonymous private information retrieval based on quantum key distribution. IEEE Trans. Inf. Forens Secur. 18, 4034–4045 (2023)

  55. Yang, Y.-G., Yang, J.-J., Zhou, Y.-H., et al.: Quantum network communication: A discrete-time quantum-walk approach. Sci. Chin. Inf. Sci. 61, 042501 (2018)

  56. Yang, Y.-G., Wang, Y.-C., Yang, Y.-L., Chen, X.-B., Li, D., Zhou, Y.-H., Shi, W.-M.: Participant attack on the deterministic measurement-device-independent quantum secret sharing protocol. Sci. Chin. Phys. Mech. Astron. 64(6), 121–124 (2021)

  57. Yang, Y.-G., Wen, Q.-Y.: Threshold multiparty quantum-information splitting via quantum channel encryption. Int. J. Quantum Inf. 07(06), 1249–1254 (2009)

  58. Yang, Y.-G., Li, B.-R., Li, D, et al.: New quantum key agreement protocols based on Bell states. Quantum Inf. Process. 18(10), 322 (2019)

  59. Yang, Y.-G., Li, B.-R., Kang, S.-Y., et al.: New quantum key agreement protocols based on cluster states. Quantum Inf. Process. 18(2), 77 (2019)

  60. Yang, Y.-G., Zhi-Chao Liu, Jian Li, Xiu-Bo Chen, Hui-Juan Zuo, Yi-Hua Zhou, Wei-Min Shi. Theoretically extensible quantum digital signature with starlike cluster states. Quantum Inf. Process. 16(1), 2 (2017)

  61. Yang, Y.-G., Gao, S., Li, D., et al.: Three-party quantum secret sharing against collective noise. Quantum Inf. Process. 18(5), 215 (2019)

  62. Yang, Y.-G., Gao, S., Li, D., et al.: New secure quantum dialogue protocols over collective noisy channels. Int. J. Theor. Phys. 58(9), 2810–2822 (2019)

Download references

Acknowledgements

This work was supported by Beijing Natural Science Foundation (Grant No. 4252014); National Natural Science Foundation of China (Grant No. 62171264); and Shandong Provincial Natural Science Foundation (ZR2023MF080).

Author information

Authors and Affiliations

  1. College of Computer Science and Technology, Beijing University of Technology, Beijing, 100124, China

    Yu-Guang Yang, Shi Qiu & Yue-Chao Wang

  2. College of Computer Science and Engineering, Shandong University of Science and Technology, Qingdao, 266590, China

    Guang-Bao Xu

  3. College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao, 266590, China

    Dong-Huan Jiang

Authors
  1. Yu-Guang Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Shi Qiu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yue-Chao Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Guang-Bao Xu
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Dong-Huan Jiang
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

Yu-Guang Yang (Methodology: Equal; Writing—original draft: Equal) Shi Qiu (Conceptualization: Lead; Investigation: Lead; Validation: Lead; Visualization: Lead; Writing—original draft: Equal) Yue-Chao Wang (Methodology: Equal; Resources: Equal) Guang-Bao Xu (Supervision: Equal; Writing—review and editing: Equal) Donghuan Jiang (Funding acquisition: Lead; Writing–review and editing: Equal).

Corresponding author

Correspondence to Yu-Guang Yang.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, YG., Qiu, S., Wang, YC. et al. A novel lottery protocol based on quantum blockchain. Quantum Inf Process 24, 32 (2025). https://doi.org/10.1007/s11128-025-04657-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-025-04657-1

Keywords