Skip to main content

Advertisement

Springer Nature Link
Log in

Nonreciprocal entanglement and asymmetric steering via magnon Kerr effect in cavity optomagnonic system

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

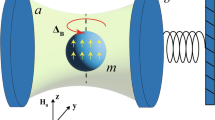
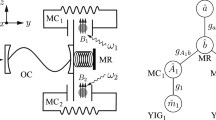
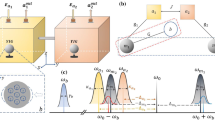
We present a scheme to generate nonreciprocal entanglement and asymmetric steering between an atomic ensemble and a magnon based on Kerr nonlinearity of magnon in an yttrium iron garnet sphere. In particular, a cavity optomagnonic system is under our consideration, where the optical cavity couples with an ensemble of N two-level atoms, and meanwhile nonlinearly interacts with the magnon mode via optomagnonic coupling. The results demonstrate that the steady-state macroscopic quantum correlations including magnon-atomic ensemble entanglement and Einstein–Podolsky–Rosen steering could be obtained via strongly driving the cavity mode. More importantly, tuning the direction of the static magnetic field leads to a positive or negative magnon Kerr coefficient, which leads to a corresponding shift in magnon frequency and thus induces the nonreciprocity of entanglement. Furthermore, the one-way steering between magnon and atomic ensemble is also shown via properly choosing the coupling strengths and effective Kerr parameters. Our work could have potential applications in the preparation of macroscopic quantum states and be applied to construct long-distance quantum networks.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

Data Availability

This manuscript has no associated data.

References

  1. Horodecki, R., Horodecki, P., Horodecki, M., Horodecki, K.: Quantum entanglement. Rev. Mod. Phys. 81(2), 865–942 (2009)

    ADS  MathSciNet  MATH  Google Scholar 

  2. Leggett, A.J.: Macroscopic quantum systems and the quantum theory of measurement. Prog. Theor. Phys. Suppl. 69, 80–100 (1980)

    ADS  MathSciNet  MATH  Google Scholar 

  3. Jeong, H., Lim, Y., Kim, M.: Coarsening measurement references and the quantum-to-classical transition. Phys. Rev. Lett. 112(1), 010402 (2014)

    ADS  MATH  Google Scholar 

  4. Fröwis, F., Sekatski, P., Dür, W., Gisin, N., Sangouard, N.: Macroscopic quantum states: measures, fragility, and implementations. Rev. Mod. Phys. 90(2), 025004 (2018)

    ADS  MathSciNet  MATH  Google Scholar 

  5. Julsgaard, B., Kozhekin, A., Polzik, E.S.: Experimental long-lived entanglement of two macroscopic objects. Nature 413(6854), 400–403 (2001)

    ADS  MATH  Google Scholar 

  6. Krauter, H., Muschik, C.A., Jensen, K., Wasilewski, W., Petersen, J.M., Cirac, J.I., Polzik, E.S.: Entanglement generated by dissipation and steady state entanglement of two macroscopic objects. Phys. Rev. Lett. 107(8), 080503 (2011)

    ADS  Google Scholar 

  7. Thomas, R.A., Parniak, M., Østfeldt, C., Møller, C.B., Bærentsen, C., Tsaturyan, Y., Schliesser, A., Appel, J., Zeuthen, E., Polzik, E.S.: Entanglement between distant macroscopic mechanical and spin systems. Nat. Phys. 17(2), 228–233 (2021)

    Google Scholar 

  8. Kotler, S., Peterson, G.A., Shojaee, E., Lecocq, F., Cicak, K., Kwiatkowski, A., Geller, S., Glancy, S., Knill, E., Simmonds, R.W., et al.: Direct observation of deterministic macroscopic entanglement. Science 372(6542), 622–625 (2021)

    ADS  Google Scholar 

  9. Lépinay, L., Ockeloen-Korppi, C.F., Woolley, M.J., Sillanpää, M.A.: Quantum mechanics-free subsystem with mechanical oscillators. Science 372(6542), 625–629 (2021)

    ADS  MathSciNet  MATH  Google Scholar 

  10. Schrödinger, E.: Discussion of probability relations between separated systems. In: Mathematical Proceedings of the Cambridge Philosophical Society, vol. 31, pp. 555–563 (1935). Cambridge University Press

  11. Einstein, A., Podolsky, B., Rosen, N.: Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47(10), 777 (1935)

    ADS  MATH  Google Scholar 

  12. Wiseman, H.M., Jones, S.J., Doherty, A.C.: Steering, entanglement, nonlocality, and the einstein-podolsky-rosen paradox. Phys. Rev. Lett. 98(14), 140402 (2007)

    ADS  MathSciNet  MATH  Google Scholar 

  13. Händchen, V., Eberle, T., Steinlechner, S., Samblowski, A., Franz, T., Werner, R.F., Schnabel, R.: Observation of one-way einstein-podolsky-rosen steering. Nat. Photonics 6(9), 596–599 (2012)

    Google Scholar 

  14. Wollmann, S., Walk, N., Bennet, A.J., Wiseman, H.M., Pryde, G.J.: Observation of genuine one-way Einstein–Podolsky–Rosen steering. Phys. Rev. Lett. 116(16), 160403 (2016)

    ADS  Google Scholar 

  15. Tischler, N., Ghafari, F., Baker, T.J., Slussarenko, S., Patel, R.B., Weston, M.M., Wollmann, S., Shalm, L.K., Verma, V.B., Nam, S.W., et al.: Conclusive experimental demonstration of one-way Einstein–Podolsky–Rosen steering. Phys. Rev. Lett. 121(10), 100401 (2018)

    ADS  Google Scholar 

  16. Qu, R., Zhang, C., Chang, Z.-H., Zhang, X.-L., Guo, Y., Hu, X.-M., Li, C.-F., Guo, G.-C., Zhang, P., Liu, B.-H.: Observation of diverse asymmetric structures in high-dimensional Einstein–Podolsky–Rosen steering. Phys. Rev. Lett. 132, 210202 (2024)

    ADS  MathSciNet  MATH  Google Scholar 

  17. Liao, C.-G., Xie, H., Chen, R.-X., Ye, M.-Y., Lin, X.-M.: Controlling one-way quantum steering in a modulated optomechanical system. Phys. Rev. A 101(3), 032120 (2020)

    ADS  MathSciNet  Google Scholar 

  18. Huang, X., Zeuthen, E., Gong, Q., He, Q.: Engineering asymmetric steady-state Einstein–Podolsky–Rosen steering in macroscopic hybrid systems. Phys. Rev. A 100(1), 012318 (2019)

    ADS  Google Scholar 

  19. Zhong, W., Zhao, D., Cheng, G., Chen, A.: One-way Einstein–Podolsky–Rosen steering of macroscopic magnons with squeezed light. Opt. Commun. 497, 127138 (2021)

    MATH  Google Scholar 

  20. Sun, F., Mao, D., Dai, Y., Ficek, Z., He, Q., Gong, Q.: Phase control of entanglement and quantum steering in a three-mode optomechanical system. New J. Phys. 19(12), 123039 (2017)

    ADS  MATH  Google Scholar 

  21. Wu, S.-X., Bai, C.-H., Li, G., Yu, C.-S., Zhang, T.: Enhancing the quantum entanglement and EPR steering of a coupled optomechanical system with a squeezed vacuum field. JOSAB 40(11), 2885–2893 (2023)

    ADS  MATH  Google Scholar 

  22. Soykal, Ö.O., Flatté, M.: Strong field interactions between a nanomagnet and a photonic cavity. Phys. Rev. Lett. 104(7), 077202 (2010)

    ADS  MATH  Google Scholar 

  23. Soykal, Ö., Flatté, M.: Size dependence of strong coupling between nanomagnets and photonic cavities. Phys. Rev. B 82(10), 104413 (2010)

    ADS  MATH  Google Scholar 

  24. Bloch, F.: Zur theorie des ferromagnetismus. Z. Phys. 61(3), 206–219 (1930)

    ADS  MATH  Google Scholar 

  25. Kong, C.: Study and application of optical transport effects in microcavity photon-phonon/magnon coupling systems. Master’s thesis, Huazhong University of Science and Technology (2020)

  26. Zhang, X., Zou, C.-L., Jiang, L., Tang, H.X.: Strongly coupled magnons and cavity microwave photons. Phys. Rev. Lett. 113(15), 156401 (2014)

    ADS  Google Scholar 

  27. Hisatomi, R., Osada, A., Tabuchi, Y., Ishikawa, T., Noguchi, A., Yamazaki, R., Usami, K., Nakamura, Y.: Bidirectional conversion between microwave and light via ferromagnetic magnons. Phys. Rev. B 93(17), 174427 (2016)

    ADS  MATH  Google Scholar 

  28. Haigh, J., Nunnenkamp, A., Ramsay, A., Ferguson, A.: Triple-resonant brillouin light scattering in magneto-optical cavities. Phys. Rev. Lett. 117(13), 133602 (2016)

    ADS  MATH  Google Scholar 

  29. Viola Kusminskiy, S., Tang, H.X., Marquardt, F.: Coupled spin-light dynamics in cavity optomagnonics. Phys. Rev. A 94(3), 033821 (2016)

    ADS  MATH  Google Scholar 

  30. Li, J., Zhu, S.-Y., Agarwal, G.: Magnon-photon-phonon entanglement in cavity magnomechanics. Phys. Rev. Lett. 121(20), 203601 (2018)

    ADS  Google Scholar 

  31. Zhang, X., Zou, C.-L., Jiang, L., Tang, H.X.: Cavity magnomechanics. Sci. Adv. 2(3), 1501286 (2016)

    ADS  Google Scholar 

  32. Zhang, G., Wang, Y., You, J.: Theory of the magnon kerr effect in cavity magnonics. Sci. China Phys. Mech. Astron. 62, 1–11 (2019)

    MATH  Google Scholar 

  33. Xiong, W., Tian, M., Zhang, G.-Q., You, J.: Strong long-range spin-spin coupling via a kerr magnon interface. Phys. Rev. B 105(24), 245310 (2022)

    ADS  MATH  Google Scholar 

  34. Ji, F.-Z., An, J.-H.: Kerr nonlinearity induced strong spin-magnon coupling. Phys. Rev. B 108(18), 180409 (2023)

    ADS  Google Scholar 

  35. Liu, G., Xiong, W., Ying, Z.-J.: Switchable superradiant phase transition with kerr magnons. Phys. Rev. A 108(3), 033704 (2023)

    ADS  Google Scholar 

  36. Zhang, G.-Q., Wang, Y., Xiong, W.: Detection sensitivity enhancement of magnon kerr nonlinearity in cavity magnonics induced by coherent perfect absorption. Phys. Rev. B 107(6), 064417 (2023)

    ADS  Google Scholar 

  37. Miao, Q., Agarwal, G.: Kerr nonlinearity induced nonreciprocity in dissipatively coupled resonators. Phys. Rev. Res. 6(3), 033020 (2024)

    Google Scholar 

  38. Flamini, F., Spagnolo, N., Sciarrino, F.: Photonic quantum information processing: a review. Rep. Prog. Phys. 82(1), 016001 (2018)

    ADS  MATH  Google Scholar 

  39. Maayani, S., Dahan, R., Kligerman, Y., Moses, E., Hassan, A.U., Jing, H., Nori, F., Christodoulides, D.N., Carmon, T.: Flying couplers above spinning resonators generate irreversible refraction. Nature 558(7711), 569–572 (2018)

    ADS  Google Scholar 

  40. Yang, J., Zhao, C., Yang, Z., Peng, R., Chao, S., Zhou, L.: Nonreciprocal ground-state cooling of mechanical resonator in a spinning optomechanical system. Front. Phys. 17(5), 52507 (2022)

    ADS  MATH  Google Scholar 

  41. Wang, X., Huang, K.-W., Xiong, H.: Nonreciprocal sideband responses in a spinning microwave magnomechanical system. Opt. Express 31(4), 5492–5506 (2023)

    ADS  MATH  Google Scholar 

  42. Jiao, Y.-F., Zhang, S.-D., Zhang, Y.-L., Miranowicz, A., Kuang, L.-M., Jing, H.: Nonreciprocal optomechanical entanglement against backscattering losses. Phys. Rev. Lett. 125(14), 143605 (2020)

    ADS  Google Scholar 

  43. Huang, Z.-H., Jiao, Y.-F., Yan, L.-L., Wang, D.-Y., Su, S.-L., Jing, H.: Nonreciprocal enhancement of macroscopic entanglement with noise tolerance. Phys. Rev. A 110(1), 012423 (2024)

    MathSciNet  MATH  Google Scholar 

  44. Bin, Q., Jing, H., Wu, Y., Nori, F., Lü, X.-Y.: Nonreciprocal bundle emissions of quantum entangled pairs. Phys. Rev. Lett. 133(4), 043601 (2024)

    MATH  Google Scholar 

  45. Wang, M., Kong, C., Sun, Z.-Y., Zhang, D., Wu, Y.-Y., Zheng, L.-L.: Nonreciprocal high-order sidebands induced by magnon kerr nonlinearity. Phys. Rev. A 104(3), 033708 (2021)

    ADS  MathSciNet  MATH  Google Scholar 

  46. Zheng, Q., Zhong, W., Cheng, G., Chen, A.: Nonreciprocal macroscopic tripartite entanglement in atom-optomagnomechanical system. EPJ Quantum Technol. 11(1), 1–14 (2024)

    MATH  Google Scholar 

  47. Kong, D., Xu, J., Wang, F.: Nonreciprocal entanglement of ferrimagnetic magnons and nitrogen-vacancy-center ensembles by kerr nonlinearity. Phys. Rev. Appl. 21(3), 034061 (2024)

    ADS  Google Scholar 

  48. Li, B., Huang, R., Xu, X., Miranowicz, A., Jing, H.: Nonreciprocal unconventional photon blockade in a spinning optomechanical system. Photon. Res. 7(6), 630–641 (2019)

    MATH  Google Scholar 

  49. Genes, C., Vitali, D., Tombesi, P.: Emergence of atom-light-mirror entanglement inside an optical cavity. Phys. Rev. A 77(5), 050307 (2008)

    ADS  MATH  Google Scholar 

  50. Ren, Y.l.: Nonreciprocal optical-microwave entanglement in a spinning magnetic resonator. Opt. Lett. 47(5), 1125–1128 (2022)

  51. DeJesus, E.X., Kaufman, C.: Routh-hurwitz criterion in the examination of eigenvalues of a system of nonlinear ordinary differential equations. Phys. Rev. A 35(12), 5288 (1987)

    ADS  MathSciNet  MATH  Google Scholar 

  52. Vitali, D., Gigan, S., Ferreira, A., Böhm, H., Tombesi, P., Guerreiro, A., Vedral, V., Zeilinger,f.A., Aspelmeyer, M.: Optomechanical entanglement between a movable mirror and a cavity field. Phys. Rev. Lett. 98(3), 030405 (2007)

  53. Parks, P., Hahn, V.: Stability Theory. Prentice Hall, New York (1993)

    MATH  Google Scholar 

  54. Plenio, M.B.: Logarithmic negativity: a full entanglement monotone that is not convex. Phys. Rev. Lett. 95(9), 090503 (2005)

    ADS  MathSciNet  MATH  Google Scholar 

  55. Vidal, G., Werner, R.F.: Computable measure of entanglement. Phys. Rev. A 65(3), 032314 (2002)

    ADS  MATH  Google Scholar 

  56. Adesso, G., Serafini, A., Illuminati, F.: Extremal entanglement and mixedness in continuous variable systems. Phys. Rev. A 70(2), 022318 (2004)

    ADS  MATH  Google Scholar 

  57. Simon, R.: Peres-horodecki separability criterion for continuous variable systems. Phys. Rev. Lett. 84(12), 2726 (2000)

    ADS  MathSciNet  MATH  Google Scholar 

  58. Kogias, I., Lee, A.R., Ragy, S., Adesso, G.: Quantification of gaussian quantum steering. Phys. Rev. Lett. 114(6), 060403 (2015)

    ADS  MATH  Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grants Nos. 12465002, 12465003 and 12175199), the Natural Science Foundation of Jiangxi Province (Grant No. 20232ACB201013), and the Foundation of Department of Science and Technology of Zhejiang Province (Grant No. 2022R52047).

Author information

Authors and Affiliations

  1. Department of Applied Physics, East China Jiaotong University, Nanchang, 330013, China

    Shuqi Hu, Jiajun Liu, Guangling Cheng & Jiansong Zhang

  2. Department of Physics, Zhejiang Sci-Tech University, Hangzhou, 310018, China

    Aixi Chen

Authors
  1. Shuqi Hu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jiajun Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Guangling Cheng
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Jiansong Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Aixi Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding authors

Correspondence to Guangling Cheng or Aixi Chen.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hu, S., Liu, J., Cheng, G. et al. Nonreciprocal entanglement and asymmetric steering via magnon Kerr effect in cavity optomagnonic system. Quantum Inf Process 24, 39 (2025). https://doi.org/10.1007/s11128-025-04658-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-025-04658-0

Keywords