Skip to main content

Advertisement

Springer Nature Link
Log in

Novel quantum voting protocol for four-particle entangled states based on superdense coding

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

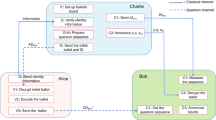
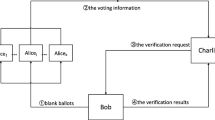
We propose a novel quantum voting protocol that utilizes superdense coding of four-particle entangled states. The protocol is simultaneously legitimate, anonymous, blind, verifiable and irreducible. In order to prevent malicious tampering of the public content, we introduce the distributed proof of work (PoW) consensus algorithm in blockchain as a database mechanism for voting participants. The voting protocol utilizes four-particle entangled states as a quantum resource to perform only single-particle operations, as well as GHZ basis measurements and \(\left\{ | 0 \rangle ,| 1\rangle \right\} \)-basis measurements. This means that our protocol can be successfully implemented using existing quantum information processing techniques. We conduct simulation experiments on the proposed voting protocol on the IBM Qiskit platform, and the results show that it is correct and feasible.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data Availability

The datasets analyzed during the current study are available from the corresponding author on reasonable request.

References

  1. Simpson, V., Oliver, M.: Electronic voting systems for lectures then and now: a comparison of research and practice. Australas. J. Educ. Tech. 23(2), 187–208 (2007)

    Article  MATH  Google Scholar 

  2. Gritzalis, D.A.: Principles and requirements for a secure e-voting system. Comput. Secur. 21, 539–556 (2002)

    Article  MATH  Google Scholar 

  3. Hillery, M., Ziman, M., Bužek, V., Bieliková, M.: Towards quantum-based privacy and voting. Phys. Lett. A. 349, 75–81 (2006)

    Article  ADS  MATH  Google Scholar 

  4. Vaccaro, J.A., Spring, J., Chefles, A.: Quantum protocols for anonymous voting and surveying. Phys. Rev. A. 75, 012333 (2007)

    Article  ADS  MATH  Google Scholar 

  5. Yi, Z., He, G.Q., Zeng, G.H.: Quantum voting protocol using two-mode squeezed states. Acta Phys. Sin. 58, 3166–3172 (2009)

    Article  MATH  Google Scholar 

  6. Bonanome, M., Bužek, V., Hillery, M., Ziman, M.: Toward protocols for quantum-ensured privacy and secure voting. Phys. Rev. A. 84, 022331 (2011)

    Article  ADS  MATH  Google Scholar 

  7. Horoshko, D., Kilin, S.: Quantum anonymous voting with anonymity check. Phys. Lett. A. 375(8), 1172–1175 (2011)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  8. Sharma, R.D., De, A.: Quantum voting using single qubits. Ind. J. Sci. Technol. 9(42), 032329 (2016)

    MATH  Google Scholar 

  9. Naseri, M., Gong, L.H., Houshmand, M., Matin, L.F.: An Anonymous Surveying Protocol via Greenberger-Horne-Zeilinger States. Int. J. Theor. Phys. 55, 4436–4444 (2016)

    Article  MATH  Google Scholar 

  10. Wang, Q.L., Yu, C.H., Gao, F., Qi, H.Y., Wen, Q.Y.: Self-tallying quantum anonymous voting. Phys. Rev. A. 94(2), 022333 (2016)

    Article  ADS  Google Scholar 

  11. Liu, X.H., Wen, X.J., Fan, X.C., Fang, J.B.: A secure quantum voting protocol based on four-particle GHZ states. Chin. J. Quantum Electron. 34, 721–727 (2017)

    MATH  Google Scholar 

  12. Wen, Q.Y., Qin, S.J., Gao, F.: Cryptanalysis of quantum cryptographic protocols. J. Cryptol. Res. 1, 200–210 (2014)

    MATH  Google Scholar 

  13. Niu, X.F., Zhang, J.Z., Xie, S.C., Chen, B.Q.: An improved quantum voting scheme. Int. J. Theor. Phys. 57, 3200–3206 (2018)

    Article  MATH  Google Scholar 

  14. Thapliyal, K., Sharma, R.D., Pathak, A.: Protocols for quantum binary voting. Int. J. Quantum Inf. 15, 1750007 (2017)

    Article  MATH  Google Scholar 

  15. Qin, J.Q., Shi, R.H., Zhang, R.: Quantum voting protocol based on controlled Quantum-Secure direct communication. Chin. J. Quantum Electron. 35, 558–566 (2018)

    MATH  Google Scholar 

  16. Qiu, C., Zhang, S.B., Chang, Y., Huang, X., Chen, H.: Electronic voting scheme based on a quantum ring signature. Int. J. Theor. Phys. 60, 1550–1555 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  17. Qiu, S.J., Xin, X.J., Zheng, Q., Li, C.Y., Li, F.G.: Security analysis and improvements on a semi-quantum electronic voting protocol. Int. J. Theor. Phys. 63, 79 (2024)

    Article  MathSciNet  MATH  Google Scholar 

  18. Xu, Y.P., Gao, D.Z., Liang, X.Q., Xu, G.B.: Semi-quantum voting protocol. Int. J. Theor. Phys. 61, 78 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  19. Yamagami, T., Segawa, E., Konno, N.: General condition of quantum teleportation by one-dimensional quantum walks. Quantum Inf. Process. 20, 224 (2021)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  20. Li, H.W., Zhang, C.M., Jiang, M.S.: Improving the performance of practical decoy-state quantum key distribution with advantage distillation technology. Commun. Phys. 5, 53 (2022)

    Article  MATH  Google Scholar 

  21. Bennett, C.H., Wiesner, S.J.: Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states. Phys. Rev. Lett. 69, 2881–2884 (1992)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  22. Bennett, C.H., Brassard, G.: Quantum cryptography: public-key distribution and coin tossing. Theor. Comput. Sci. 561(1), 7–11 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  23. Mayers, D.: Unconditional security in quantum cryptography. J. ACM. 48, 351–406 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  24. Shor, P.W., Preskill, J.: Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 85, 441–444 (2000)

    Article  ADS  MATH  Google Scholar 

  25. Lo, H.K., Chau, H.F.: Unconditional security of quantum key distribution over arbitrarily long distances. Science 283, 2050–2056 (1999)

    Article  ADS  MATH  Google Scholar 

  26. Wang, Y.: One-time pad security and new confidentiality system. Netinfo Secur. 41–43 (2004)

  27. Rubin, F.: One-time pad cryptography. Cryptologia 20, 359–364 (1996)

    Article  MATH  Google Scholar 

  28. Wei, C.Y., Cai, X.Q., Wang, T.Y., Qin, S.J., Gao, F., Wen, Q.Y.: Error tolerance bound in QKD-based quantum private query. IEEE J. Sel. Area. Comm. 38(3), 517–527 (2020)

    Article  MATH  Google Scholar 

  29. Wang, T.Y., Cai, X.Q., Ren, Y.L., Zhang, R.L.: Security of quantum digital signatures for classical messages. Sci. Rep. 5, 9231 (2015)

    Article  MATH  Google Scholar 

  30. Sun, X., Wang, Q., Kulicki, P., Sopek, M.: A simple voting protocol on quantum blockchain. Int. J. Theor. Phys. 58, 275–281 (2019)

    Article  MATH  Google Scholar 

  31. Ryan, P.Y.A., Bismark, D., Heather, J., Schneider, S.: Zhe Xia: PrEt À Voter: a voter-verifiable voting system. IEEE Trans. Inf. Foren. Sec. 4, 662–673 (2009)

    Article  MATH  Google Scholar 

  32. Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: Proceedings 42nd IEEE Symposium on Foundations of Computer Science. pp. 136–145. IEEE, Newport Beach, CA, USA (2001)

  33. Jiang, D.H., Xu, G.B.: Multiparty quantum key agreement protocol based on locally indistinguishable orthogonal product states. Quantum Inf. Process. 17, 180 (2018)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  34. Cao, H.J., Ding, L.Y., Jiang, X.L., Li, P.F.: A new proxy electronic voting scheme achieved by six-particle entangled states. Int. J. Theor. Phys. 57, 674–681 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  35. Wang, J., Xu, G.B., Jiang, D.H.: Quantum voting scheme with Greenberger-Horne-Zeilinger States. Int. J. Theor. Phys. 59, 2599–2605 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  36. Tian, J.H., Zhang, J.Z., Li, Y.P.: A quantum multi-proxy blind signature scheme based on genuine four-qubit entangled state. Int. J. Theor. Phys. 55, 809–816 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  37. Zhang, J.L., Zhang, J.Z., Xie, S.C.: A Choreographed Distributed Electronic Voting Scheme. Int. J. Theor. Phys. 57, 2676–2686 (2018)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Funding

This work is supported by the National Natural Science Foundation of China (Grant No. 62171264) and Shandong Provincial Natural Science Foundation (Grant No.ZR2023MF080).

Author information

Authors and Affiliations

  1. College of Computer Science and Engineering, Shandong University of Science and Technology, Qingdao, 266590, Shandong, China

    Hao-Wen Zhang & Guang-Bao Xu

  2. College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao, 266590, Shandong, China

    Dong-Huan Jiang

Authors
  1. Hao-Wen Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Guang-Bao Xu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Dong-Huan Jiang
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

All authors contributed equally to the paper.

Corresponding author

Correspondence to Dong-Huan Jiang.

Ethics declarations

Conflict of interest

All authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this manuscript.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, HW., Xu, GB. & Jiang, DH. Novel quantum voting protocol for four-particle entangled states based on superdense coding. Quantum Inf Process 24, 44 (2025). https://doi.org/10.1007/s11128-025-04663-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-025-04663-3

Keywords