Abstract
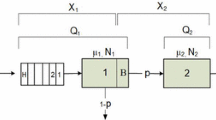
Consider a tandem queue of two single-server stations with only one server for both stations, who may allocate a fraction α of the service capacity to station 1 and 1−α to station 2 when both are busy. A recent paper treats this model under classical Poisson, exponential assumptions.
Using work conservation and FIFO, we show that on every sample path (no stochastic assumptions), the waiting time in system of every customer increases with α. For Poisson arrivals and an arbitrary joint distribution of service times of the same customer at each station, we find the average waiting time at each station for α = 0 and α = 1. We extend these results to k ≥ 3 stations, sample paths that allow for server breakdown and repair, and to a tandem arrangement of single-server tandem queues.
Similar content being viewed by others
References
H.-S. Ahn, I. Duenyas and M.E. Lewis, Optimal control of a two-stage tandem queuing system with flexible servers, Probability in the Engineering and Information Sciences 16 (2002) 453–469.
H.-S. Ahn, I. Duenyas and R.Q. Zhang, Optimal stochastic scheduling of a two-stage tandem queue with parallel servers, Adv. Appl. Prob. 31 (1999) 1095–1117.
I. Duenyas, D. Gupta and T.L. Olsen, Control of a single-server tandem queueing system with setups, Oper. Res. 46 (1998) 218–230.
S.M.R. Irvani, M.J.M. Posner and J.A. Buzacott, A two-stage tandem queue attended by a moving server with holding and switching costs, Queueing Systems 26 (1997) 203–228.
P.K. Johri and M.N. Katehakis, Scheduling service in tandem qeues attended by a single server, Stochastic Anal. 6 (1988) 279–288.
G. Koole and R. Righter, Optimal control of tandem reentrant queues, Queueing Systems 28 (1998) 337–347.
R.T. Nelson, Dual-resource constrained series service systems, Oper. Res. 16 (1968) 324–341.
R.M. Oliver and A.H. Samuel, Reducing letter delays in post offices, Oper. Res. 10 (1962) 839–892.
J. Resing and L. Örmeci, A tandem queueing model with coupled processors, Oper. Res. Let. 31 (2003) 383–389.
M. Taube-Netto, Two queues in tandem attended by a single server, Oper. Res. 25 (1977) 140–147.
M.P. Van Oyen, E.G.S. Gel and W.J. Hopp, Performance opportunity for workforce agility in collaborative and noncollaborative work systems, IIE Transactions 33 (2001) 761–777.
R.W. Wolff, Tandem queues with dependent service times in light traffic, Oper. Res. 30 (1982) 619–635.
R.W. Wolff, Stochastic Modeling and the Theory of Queues (Prentice-Hall, Englewood Cliffs, NJ, 1989).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Wang, CL., Wolff, R.W. Work-Conserving Tandem Queues. Queueing Syst 49, 283–296 (2005). https://doi.org/10.1007/s11134-005-6968-7
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/s11134-005-6968-7